В работе изучаются операции на классах конечных групп. Установлены свойства операции
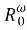
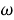
Ключевые слова: группа, конечная группа, класс групп, операция на классах групп .
Введение
Теория конечных групп является одним из интенсивно развивающихся направлений современной алгебры (см., например, [4, 9]). В 30-е годы ХХ века в рамках теории групп сформировалось новое направление — теория классов групп (см., например, [3, 8]). В алгебре важным аспектом исследования рассматриваемых объектов является изучение операций над данными объектами. В этой связи с развитием теории классов групп актуальным стал вопрос введения в рассмотрение и изучение операций над классами групп [1].
В настоящее время хорошо известными и наиболее изученными являются такие операции на классах групп, как операции
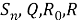
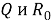
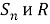
В современной теории классов групп центральное место занимают локальные формации и локальные классы Фиттинга [5]. Понятие
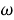
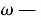
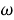
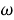
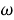
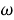
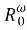
Предварительные сведения
В доказательствах теорем используются классические методы теории групп, а также методы теории классов групп. Рассматриваются только конечные группы. Используемые обозначения и определения для групп и классов групп стандартны. Приведем лишь некоторые из них.
Символ ∃ означает квантор существования (произносится «существует» или «для некоторого»), символ
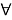
Непустое множество
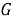

1) ассоциативность операции

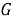
2)
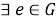
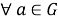
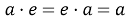
3)
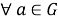
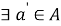
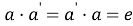
Запись

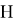
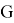
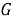
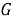
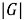
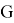

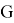
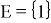
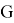
Группы
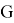
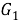
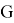
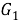
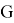
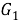
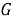
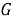
Операцией на классах групп
называется отображение множества всех классов групп в себя. Пусть
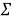
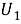
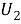
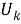
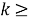
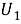
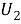
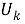
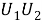
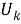
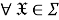
1)
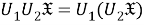
2)
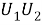
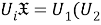
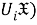
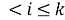
Пусть
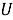
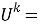
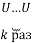
Пусть
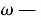
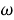
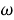
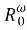
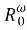
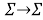
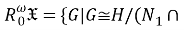
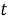
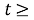
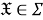
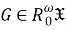
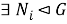
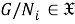
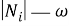
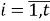
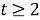
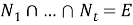
Основные результаты
В теореме 1 установлена взаимосвязь между классами
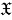
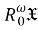
Теорема 1.
Пусть
𝔛 —
произвольный класс групп
.
Тогда
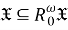
Доказательство.
Пусть
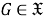
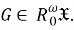
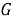
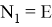
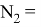
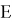
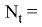
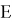
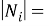
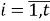
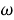
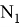
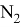
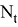
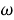
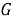
Так как
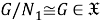
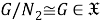
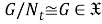
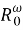
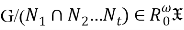
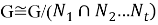
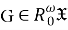
Таким образом,
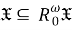
В теореме 2 установлена взаимосвязь между классами
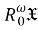
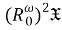
Теорема 2.
Пусть
𝔛 —
произвольный класс групп
.
Тогда
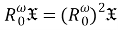
Доказательство.
Установим, что
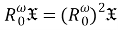
а) Покажем, что
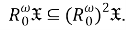
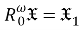
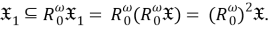
Следовательно,
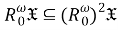
б) Проверим, что
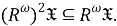
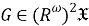
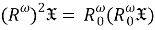
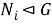
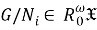
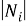
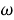
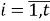
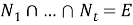
Поскольку
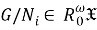
(
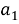
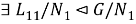
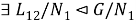
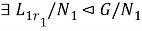
(
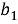
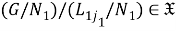
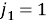
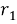
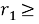
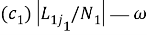
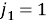
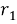
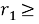
(
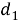
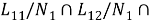
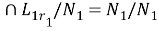
и так далее,
(
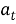
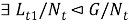
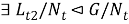
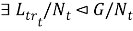
(
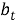
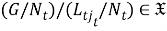
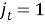
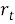
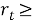
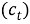
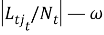
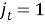
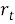
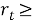
(
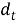
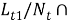
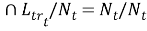
Из (
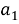
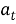
(
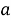
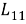
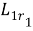
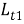
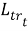
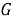
Из (
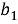
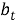
(
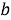
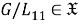
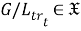
Из (
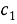
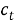
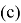
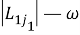
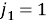
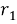
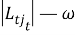
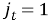
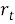
Из (
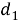
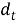
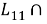
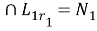
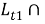
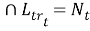
(
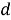
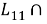
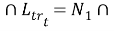
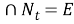
Из (
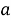
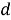
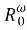
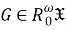
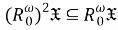
Из а) и б) получаем равенство
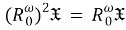
Заключение
Операция
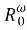
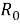
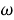
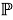
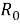
Литература:
- Ведерников В. А. Элементы теории классов групп. — Смоленск: Смоленская городская типография, 1988. 96 с.
- Воробьев Н. Н. Алгебра классов конечных групп. — Витебск: ВГУ имени П. М. Машерова, 2012. 322 с.
- Каморников С. Ф., Селькин М. В. Подгрупповые функторы и классы конечных групп. — Минск: Беларуская навука, 2003. 254 с.
- Монахов В. С. Введение в теорию конечных групп и их классов. — Минск: Высшая школа, 2006. 207 с.
- Скиба А. Н. Алгебра формаций. — Минск: Беларуская навука, 1997. 240 с.
-
Скиба А. Н., Шеметков Л. А. Кратно
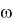
- Шеметков Л. А. Формации конечных групп. — М.: Наука, 1978. 272 с.
- Doerk K., Нawkes T. Finite soluble groups. — Berlin — New York: Walter de Gruyter, 1992. 891 p.
- Guo W. The Theory of Classes of Groups. — Beijing — New York: Science Press, 2000. 258 p.

