Outer invariants of periodic *-automorphisms of AW*-factors
В настоящее время в функциональном анализе получило широкое распространение изучение алгебр операторов, действующих в гильбертовом пространстве, так как они описывают модель эволюции квантово-механической физической системы. Однако широкому изучению подверглись С*- и W*-алгебры, известные также как алгебры фон Неймана, в то время как алгебрам Капланского, они же AW*-алгебры, посвящено очень мало работ, особенно в русскоязычном секторе научных работ. Изучение AW*-алгебр усложнено тем, что не все свойства, которыми обладают хорошо изученные W*-алгебры можно применить к AW*-алгебрам, которые являются расширением W*-алгебр.
Теория алгебр операторов, действующих в гильбертовом пространстве, возникла в 30-е годы с появлением серии статей Джона фон Неймана и Мюррея. Главными мотивировками этих авторов были применение некоторых аспектов квантово-механического формализма, согласно которым наблюдаемой физической системе соответствует линейный самосопряженный оператор, действующий в гильбертовом пространстве, а всякому состоянию рассматриваемой физической системы соответствует матрица плотности, действующая в гильбертовом пространстве. Как известно, автоморфизмы операторных алгебр — это не что иное, как эволюция данной физической системы. Следовательно, результаты, касающиеся автоморфизмов операторных алгебр, в частности, их классификация, с точностью до сопряженности, этих отображений имеют соответствующие интерпретации в квантовой механике и математической физике. Поэтому изучение автоморфизмов операторных алгебр является достаточно актуальным.
Автоморфизмы алгебр фон Неймана достаточно хорошо изучены. Получена полная классификация периодических автоморфизмов конечных факторов и, с точностью до внешней сопряженности, получено описание внешне сопряженных классов автоморфизмов алгебр фон Неймана. Основные достижения в этом направление, получены в работах французского математика Алана Конна, за которые он, в 1982 году, получил Филдсовскую награду. Поскольку AW*-алгебры являются обобщением (расширением) алгебр фон Неймана, то естественно возникает вопрос об обобщение результатов Алана Конна для этих алгебр. Поэтому изучение автоморфизмов AW*-алгебр, то есть расширение результатов, полученных для алгебр фон Неймана к AW*-алгебрам является также достаточно актуальным.
В данной статье следуя по статье Алана Конна [1], подробно рассматриваются первоначальные свойства периодических *-автоморфизмов конечных AW*-факторов.
В статье даются основные понятия AW*-факторов и их *-автоморфизмов. Дается определение сопряженных и внешне сопряженных *-автоморфизмов, определены их внешние и внутренние инварианты. Доказана связь между внешними инвариантами и внешней сопряженностью *-автоморфизмов AW*-фактора.
Ключевые слова: гильбертово пространство; С*-алгебра; алгебра фон Неймана; W*-алгебра; коммутант; алгебра Капланского; AW*-алгебра; аннулятор; Бэровская *-алгебра; AW*-фактор; *-автоморфизм; внутренний *-автоморфизм; сопряженные *-автоморфизмы; внешне сопряженные *-автоморфизмы; периодические *-автоморфизмы; внешние инварианты.
At present, the study of algebras of operators acting in a Hilbert space has become widespread in functional analysis, since they describe a model of the evolution of a quantum mechanical physical system. However, C*- and W*-algebras, also known as von Neumann algebras, have been widely studied, while very few works are devoted to Kaplansky algebras, they are also AW*-algebras, especially in the Russian-speaking sector of scientific works. The study of AW*-algebras is complicated by the fact that not all the properties that well-studied W*-algebras have can be applied to AW*-algebras, which are extensions of W*-algebras.
The theory of operator algebras acting in a Hilbert space arose in the 1930s with the appearance of a series of papers by John von Neumann and Murray. The main motivations of these authors were the use of some aspects of quantum mechanical formalism, according to which an observed physical system corresponds to a linear self-adjoint operator acting in a Hilbert space, and to any state of the considered physical system there corresponds a density matrix acting in a Hilbert space. As is known, automorphisms of operator algebras are nothing but the evolution of a given physical system. Consequently, results concerning automorphisms of operator algebras, in particular, their classification, up to conjugacy, of these mappings have corresponding interpretations in quantum mechanics and mathematical physics. Therefore, the study of automorphisms of operator algebras is quite topical.
Automorphisms of von Neumann algebras are fairly well studied. A complete classification of periodic automorphisms of finite factors is obtained and, up to external conjugacy, a description is obtained of externally conjugate classes of automorphisms of von Neumann algebras. The main achievements in this direction were obtained in the works of the French mathematician Alan Conn, for which he, in 1982, received the Fields Medal. Since AW*-algebras are a generalization (extension) of von Neumann algebras, the question naturally arises about the generalization of Alan Conn's results for these algebras. Therefore, the study of automorphisms of AW*-algebras, that is, the extension of the results obtained for von Neumann algebras to AW*-algebras, is also quite relevant.
In this article, following the article by Alan Conn [1], we consider in detail the initial properties of periodic *-automorphisms of finite AW*-factors.
The article gives the basic concepts of AW*-factors and their *-automorphisms. The definition of adjoint and externally conjugate *-automorphisms is given, their external and internal invariants are determined. A connection between outer invariants and outer conjugacy of *-automorphisms of an AW*-factor is proved.
Keywords: Hilbert space; C*-algebra; von Neumann algebra; W*-algebra; commutant; Kaplansky algebra; AW*-algebra; annihilator; Baer *-algebra; AW*-factor; *-automorphism; inner *-automorphism; conjugate *-automorphisms; externally conjugate *-automorphisms; periodic *-automorphisms; external invariants.
Пусть
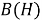
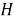
Определение 1.
W*-алгебра (алгебра фон Неймана)
— эта слабо замкнутая комплексная *-подалгебра в
B(H)
, содержащая единицу
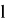
Определение 2. Алгебра M' — это множество всех элементов из B(Н) , коммутирующих со всеми элементами из M, называется коммутантом алгебры М. [5]
Определение 3.
Центр Z(M)
— это совокупность элементов алгебры М, коммутирующие с каждым элементом из этой алгебры. Легко видеть, что
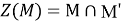
Определение 4.
W*-алгебра М называется
фактором
, если ее центр Z(M) состоит из комплексных кратных
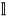
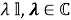
Определение 5.
Линейное отображение
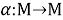
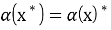
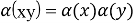
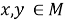
Определение 6.
*-автоморфизм
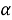
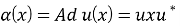
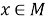
Обозначим через
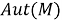
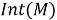
Определение 7.
Говорят, что два *-автоморфизма
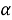
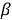
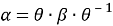
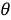
Определение 8.
C*-алгебра
— эта комплексная банахова *-алгебра А, такая что
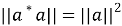
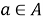
Определение 9. Пусть A — комплексная *-алгебра и пусть S — непустое подмножество А. Положим
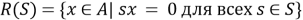
и назовем R(S) правым аннулятором S. Аналогично
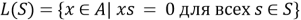
левый аннулятор S. [9]
Определение 10.
*-алгебра A называется
Бэровской *-алгеброй
, если для любого непустого
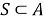
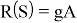
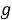
Поскольку
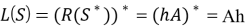
Определение 11. C*-алгебра A, которая является Бэровской *-алгеброй, называется AW* — алгеброй или алгеброй Капланского . [10]
Каждая W*-алгебра является AW*-алгеброй, однако, обратное не верно (см. [3], [4]).
Пусть в дальнейшем, N является AW*-фактором. Если α ∈ Aut( N ), то мы определим два числа, p 0 (α) и γ(α) следующим образом:
{nϵZ α n ∈ Int N}=p 0 (α) Z и p 0 (α) ∈ N,
(
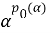
Мы видим, что для каждого α, p 0 (α) представляет собой целое число, которое мы называем внешним периодом α; это число будет 0, если все ненулевые степени α являются внешними. Существование этих чисел мы покажем ниже.
Пусть α — периодический *-автоморфизм алгебры
N
и пусть р ∈ ℕ — период α, то есть α
р
=id тождественное отображение. Тогда
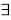
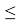
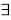
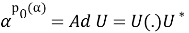
Потому что если нет такой р
0
(α), то положим р
0
(α)=р, так как в этом случае
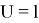
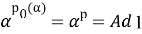
Предложение 12. Пусть N — AW*-фактор. Тогда существует комплексное число γ(α) с |γ(α)|=1, такое что α(U)= γ(α)U.
Доказательство.
Из очевидного равенства
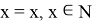
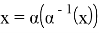
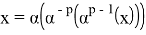
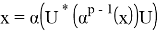
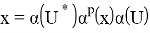
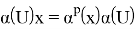
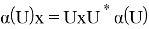
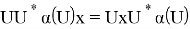
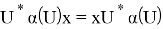
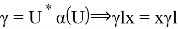
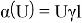
Предложение доказано.
Мы видим, что γ(α) представляет собой комплексное число, по модулю 1, и не зависит от выбора U, такое что
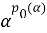
γ
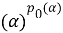
Действительно, так как
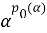
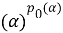
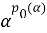
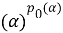
Определение 13. Отображения α и β ∈ Aut( N ) называются внешне сопряженными , если существует σ ∈ Аut( N ) такой, что β и σασ -1 имеют один и тот же образ в Out( N )=Aut( N ) / Int( N ).
Для унитарного W в N , и автоморфизма α ∈ Aut( N ) рассмотрим автоморфизм w α =Ad W⋅α=WαW*. Когда W меняется, то w α образуют класс по α в Out( N ), следовательно, β ∈ Aut( N ), которые внешне сопряжены с α.
Теперь докажем основной результат статьи.
Теорема 14. Пусть N — AW*-фактор. Если периодические *-автоморфизмы α и β — внешне сопряжены, то, их так называемые внешние инварианты совпадают, то есть р 0 (α)=р 0 (β), γ(α)=γ(β).
Доказательство. Первое равенство p 0 (α)=p 0 (β) очевидно. Для доказательства второго γ(α)=γ(β) мы можем предположить, что β= w α, для некоторого унитарного W в N . Потому что, по условию теоремы, α и β — внешне сопряжены.
Пусть
р= p 0 (α), γ=γ(α) α p = Ad U, α(U)= γU.
Тогда мы имеем
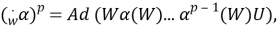
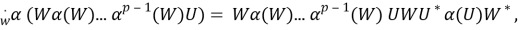
Следовательно,
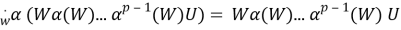
Отсюда
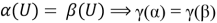
Литература:
- A.Connes. Periodic automorphisms of the hyperfinite factor of type II 1 , Acta Sci. Math., 39 (1977), 39–66
- Ayupov Sh.А., Rakhimov А. А., Usmanov Sh.M. Jordan, Real and Lie structures in operator algebras. Kluwer Academic Publishers, MAIA. 1997, Vol. 418, 235 p.
- Ayupov Sh.A., Rakhimov A. A. Real W*-algebras, Actions of groups and Index theory for real factors. VDM Publishing House Ltd. Beau-Bassin, Germany, Bonn. ISBN 978–3-639–29066–0. 2010, p.138.
- Berberian, Sterling K., Baer *-rings, Die Grundlehren der mathematischen Wissenschaften, Springer-Verlag Berlin Heidelberg 1972, 2nd printing 2011, Vol. 195, e-ISBN 978–3-642–15071–5, p.301.
- Connes A. Une classication des facteurs de type III. Ann. Sc. Ec. Norm. Sup., 1973, 6. pp. 133–252.
- Connes A. Classication of injective facteurs. Ann. Math., 1976. Vol. 104. N 1. pp. 73–115.
- Connes A. Outer conjugacy classes of automorphisms of factors. Ann. Scient. Ec. Norm. Sup., 4e serie, t. 8 1975. pp. 383–420.
- Dixmier J. Sur certains espaces consid.er.es par M. H. Stone. Summa Brasil. Math., 1951, 2, pp.151–182.
- Kaplansky I. Projections in Banach algebras. Ann. Math., 1951, 53, pp.235–249.
- Kaplansky I. Algebras of type I., Ann. Math. 1952, 56, pp. 460–472.

