Математическая модель асинхронного двигателя с переменными ψs – is на выходе интегрирующих звеньев в Simulink-Script
Емельянов Александр Александрович, доцент;
Бесклеткин Виктор Викторович, ассистент;
Кривцов Алексей Вячеславович, студент;
Чиркова Анастасия Андреевна, студент;
Дудин Александр Сергеевич, студент;
Кудимов Юрий Сергеевич, студент;
Андреева Анастасия Андреевна, студент;
Лепинских Наталия Аркадьевна, студент;
Строшкова Анастасия Викторовна, студент;
Лихачева Ирина Викторовна, студент
Российский государственный профессионально-педагогический университет (г. Екатеринбург)
Данная работа является продолжением статьи [1], в которой проекции вектора ![]() были получены на выходе апериодических звеньев. В этой статье проекции векторов
были получены на выходе апериодических звеньев. В этой статье проекции векторов ![]() и
и ![]() выведены на основе интегрирующих звеньев.
выведены на основе интегрирующих звеньев.
Для лучшего понимания логики преобразований необходимо просмотреть все предыдущие наши статьи по этой теме за 2015 г. Так как главной целью является привлечение студентов к исследовательской работе, то в соответствии с нашей традицией, выводы всех уравнений приводим без сокращений.
Приведем уравнение, связывающее векторы ![]() и
и ![]() по проекции (+1) [1]:
по проекции (+1) [1]:
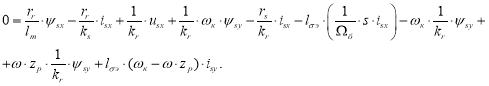 (1)
(1)
Перенесем ![]() в левую часть:
в левую часть:
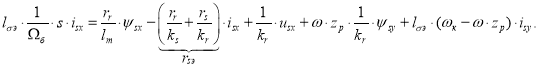
Обозначим 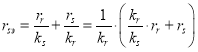 .
.
Разделим обе части на ![]() :
:
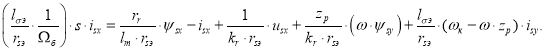
Обозначим ![]() :
:
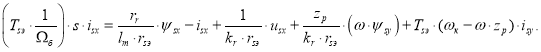
Определим ![]() :
:
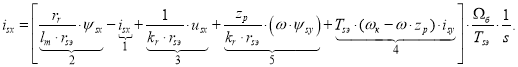 (2)
(2)
Структурная схема для реализации уравнения (2) дана на рис. 1.

Рис. 1. Структурная схема проекции вектора статорного тока ![]() на ось +1
на ось +1
Аналогично для уравнения, связывающего векторы ![]() и
и ![]() по проекции (+j) [1]:
по проекции (+j) [1]:
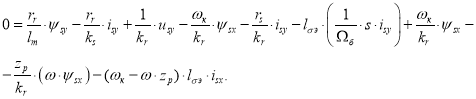 (3)
(3)
Перенесем ![]() в левую часть:
в левую часть:
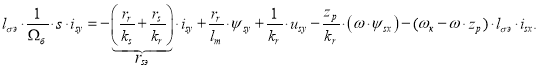
Разделим обе части полученного уравнения на ![]() :
:
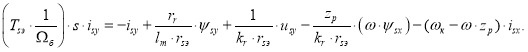
Отсюда определим ток ![]() :
:
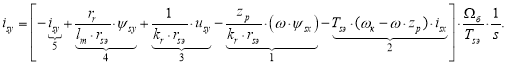 (4)
(4)
Структурная схема, соответствующая уравнению (4), показана на рис. 2.
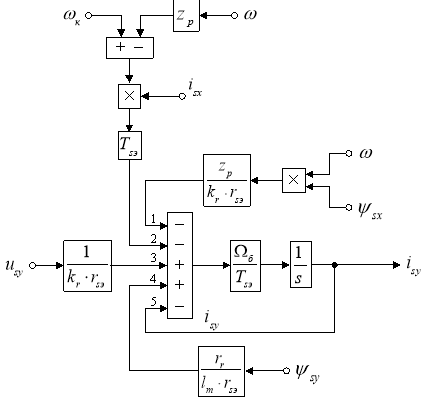
Рис. 2. Структурная схема проекции вектора статорного тока ![]() на ось +j
на ось +j
Из уравнения (1’) [1] по оси (+1) выразим ψsx:
![]()
![]()
![]() (5)
(5)
Структурная схема для уравнения (5) приведена на рис. 3.
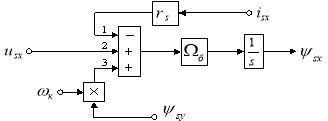
Рис. 3. Структурная схема проекции вектора потокосцепления статора ![]() на ось (+1)
на ось (+1)
Из уравнения (1”) [1] по оси (+j) выразим ψsy:
![]()
![]()
![]() (6)
(6)
Уравнению (6) соответствует структурная схема, приведенная на рис. 4.
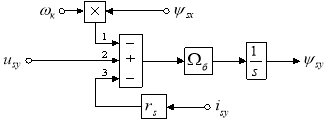
Рис. 4. Структурная схема проекции вектора потокосцепления статора ![]() на ось (+j)
на ось (+j)
На рис. 5 представлены структурные схемы для реализации уравнений электромагнитного момента и механической угловой скорости вращения вала двигателя:
![]()
![]()
![]() (7)
(7)
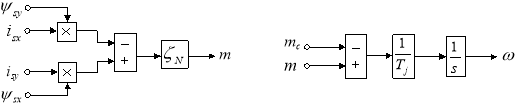
Рис. 5. Структурные схемы для определения электромагнитного момента m и механической угловой скорости вращения вала двигателя ω
Полная математическая модель асинхронного двигателя с короткозамкнутым ротором с переменными ψs – is на выходе интегрирующих звеньев приведена на рис. 7. Параметры асинхронного двигателя рассмотрены в работах [2] и [3].
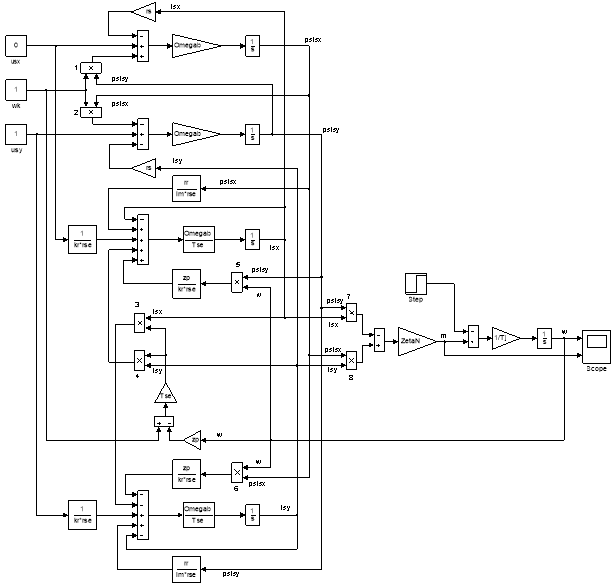
Рис. 7. Математическая модель асинхронного двигателя с переменными ψs – is на выходе интегрирующих звеньев
Расчет параметров производим в Script:
|
PN=320000; UsN=380; IsN=324; fN=50; Omega0N=104.7; OmegaN=102.83; nN=0.944; cos_phiN=0.92; zp=3; Rs=0.0178; Xs=0.118; Rr=0.0194; Xr=0.123; Xm=4.552; J=28; Ub=sqrt(2)*UsN; Ib=sqrt(2)*IsN; |
OmegasN=2*pi*fN; Omegab=OmegasN; Omegarb=Omegab/zp; Zb=Ub/Ib; Psib=Ub/Omegab; Lb=Psib/Ib; kd=1.0084; Mb=kd*PN/OmegaN; Pb=Mb*Omegarb; rs=Rs/Zb; ls=Xs/Zb; lr=Xr/Zb; lm=Xm/Zb; SsN=3*UsN*IsN; ZetaN=SsN/Pb; ks=lm/(lm+ls); kr=lm/(lm+lr); |
Tj=J*Omegarb/Mb; betaN=(Omega0N-OmegaN)/Omega0N; wN=(1-betaN); lbe=(ls+lr+ls*lr*lm^(-1)); roN=0.9962; rr=roN*betaN; alphar=kr*rr/lm; le=kr*lbe; re=rs+(kr^2)*rr; Te=le/re; Tr=(lm+lr)/rr; Psi_rN=0.942; Trb=lbe*ks/rr; Tsb=lbe*kr/rs; rse=(kr*rr/ks+rs)/kr; Tse=lbe/rse; |
Результаты моделирования асинхронного двигателя представлены на рис. 8.
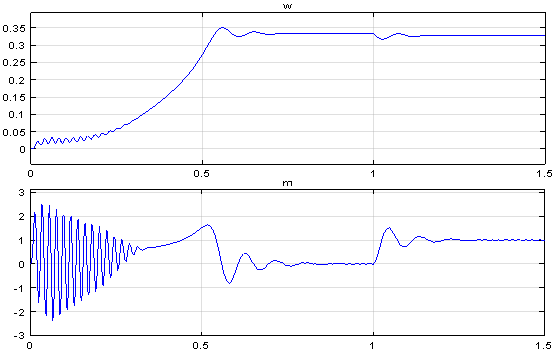
Рис. 8. Графики скорости и электромагнитного момента
Литература:
- Емельянов А. А., Бесклеткин В. В., Коновалов И. Д., Антоненко И. А., Харин В. С., Ченцова Е. В., Шевнин С. С., Федосеев П. В. Математическая модель асинхронного двигателя с переменными ψs – is в Simulink-Script // Молодой ученый. – 2016. – №21. – С. 20-30.
- Шрейнер Р. Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. – Екатеринбург: УРО РАН, 2000. – 654 с.
- Шрейнер Р. Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р. Т. Шрейнер, А. В. Костылев, В. К. Кривовяз, С. И. Шилин. Под ред. проф. д. т. н. Р. Т. Шрейнера. – Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. – 361 с.

