Осциллирующая функция



Осциллирующая функция

1. Введение

Дня изучения структуры колебательных систем рассматриваются свободные колебания абстрактной динамической системы с одной степенью свободы в сингулярном () пространстве, в котором невозможно выделить какую-либо отдельную часть и следует рассматривать только как неделимое целое . В дополнение к пространству следует его окружение — ( пространство, обратное первому), которому также присуще неделимое внутреннее содержание.

Рассмотрению подлежат свободные (невынужденные) колебания в отсутствии каких-либо сил трения (не диссипативные колебательные системы, отличающиеся постоянством энергии ).

и пространства составляют симметричную осциллирующую пару, в которой они функционально периодически заменяют друг друга за один период. иявляются единым осциллирующим образованием — колебательной системой и рассматриваются как её осцилляторы. Они дополняют друг друга, но по отдельности не существуют. Результирующее действие простейшей колебательной системы за период равно нулю, что диктуется симметрией и пространств.

Одномерный осциллятор, размер которого имеет конечное значение, обязательно ограничен в амплитуде, превышение которой размера самого осциллятора приводит к появлению нового, т. е. усложнению колебательной системы. Прежний осциллятор теперь получает ненулевое результирующее постоянное значение, а новыйосциллятор — теперь выступает в качестве . Здесь колебательная система получает этажную структуру,каждый новый осциллятор образует новый этаж.

Осциллирующая () — функция, призванная находить значения, характеризующие осцилляторы.

Колебательная система в пространстве должна описываться такой функцией, значения которой должны быть дискретны, в одномерной системе координат (с одной степенью свободы), не имеющей определённого начала отсчёта, что отвечает свойству пространства.

Система получает сложную этажную структуру, в которой каждый этаж имеет своё значение и свой осциллятор, т. е. - функция описывает систему дискретными значениями, разделёнными промежутками.

промежутки характеризуются, как сингулярные, и в нахождении собственных значений не нуждаются, но их присутствие учитывается как разница дискретных значений — функции,

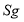2. и 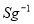пространства

Колебательные системы с одной степенью свободы должны описываться соответствующей функцией в одномерной системе координат. При этом она должна иметь две симметричные составляющие — функции, отвечающие и пространствам.

Осциллирующие пространства и , как равные по значимости, в одномерной системе координат требуют ортосимметричного представления:пространство с окружением и пространство с окружением.

-функция является -этажной, что выражается не только в количественном, но и качественном аспекте — при определённом значении у функции появляется новая составляющая - функции (рассмотрены ниже) и содержащей значение самой функции и значение её аргумента.

Каждому этажу -функции соответствует своё числовое значение (т. е. представление, не противоречащее определению функции). Значения аргументов такой функции и значения самой функции принимают дискретные значения. Интервал между двумя значениями занимает сингулярная область , размер которой может быть задан.

3 Одномерная система координат в сингулярном пространстве

Одномерная система координат задается своим началом (точкой О и в данной работе с центром ) и единственным базисным вектором, определяющим положительное направление координатной оси Ох. Координаты любой точки x в такой системе определяются одним действительным числом.

В одномерной системе координаты точек — , , .

Расстояние между двумя точками и на координатной прямой равно абсолютному значению разности их координат: — представлено сингулярным пространством.

Os — функция, размещенная в одномерной системе координат, представлена двумя дискретными числовыми массивами:

(3.1)

значения которых разделены сингулярными промежутками, кратными .

В одномерной системе координат аргумент функции и значение функции расположены на одной числовой прямой и представлена дискретной суммой значений аргумента и функции:

.(3.2)

В первом случае сумма, во втором случае разность, в противном случае массивы были бы неразличимы.

Для анализа функции обычно используется бесконечно малое, стремящееся к нулю приращение аргумента . В дискретной форме представления функции минимальное приращение равно ненулевой величине .

Допустим, что имеется аргумент непрерывной функции — и аргумент дискретной функции — , то возможность проведения анализа дискретной функции обеспечивает усложнение аргумента этой функции:

.(3.3)

Нахождение производной дискретной функции рассматривается как производная сложной функции:

.(3.4)

Функция становится сложной, но аналитической. Приведённое дифференцирование в сингулярном пространстве используется только в качестве вспомогательного и условного, для определения вида дифференциалов в рассматриваемых интегралах.

4 Уравнение колебаний в сингулярном пространстве

Уравнение колебаний должно удовлетворять дифференциальному уравнению второго порядка (Гемльгольца) :

. (4.1)

Это дифференциальное уравнение гармонических колебаний, для которого в каждой точке проверяется условие (4.1). При условии непрерывности функции — это условие определяет ряд точек, рисующих кривую гармонических колебаний.

В сингулярном осцилляторе, размер которого определён только одним значением , не существует возможности дифференциально найти кривую колебаний. Есть ли в этом необходимость при задании другого критерия в определении колебательного процесса? Здесь он диктуется следующими условиями:

• и должны быть ортонормированными, и должны быть равны в колебательном процессе:

, . (4.2)

Пределы интегрирования соответствуют условию (3.3).

• необходимость выполнения условия симметрии дифференциальных уравнений , что имеет подтверждение в интегральной форме (4.2).

Уравнение гармонических колебаний представлено интегральной формой в противовес к дифференциальной.

5 Ортонормированная система функций

Пусть имеется евклидово пространство, элементами которого являются функции аргумента , со скалярным произведением .

Система функций ,, …, называется ортогональной, если все функции системы попарно ортогональны, то есть = 0 при .

Система функций ,, …, называется ортонормированной, если она ортогональна и нормирована.

Последнее означает, что

, . (5.1)

Это соответствует условиям поставленной задачи — когда является окружением пространства и наоборот.

Таким образом, две составляющие осциллирующей функции являются ортонормированными относительно величины . В -пространствеортонормированность функций выражается не относительно какого-то числа, но относительно какого-то центра осцилляции — . Смысл этой величины будет показан ниже.

Ортонормированность выражается в интегральной симметрии описывающих и пространств, обеспечивающих выполнение условия:

, (5.2)

где является одной из первообразных функции .

За этим следует выполнение условий (4.2).

Выражения (5.3) являются уравнениями колебаний в сингулярном пространстве, которые соответствуют системе, включающей два процесса, показанные на рис, 2.1. Первое интегрирование производится в одном направлении , повторное — в ортонормированном направлении ,что и обеспечивает симметричность колебательного процесса.

6 -функция

Для искомой функции предлагается аргумент , удовлетворяющий условию (5.2):

, . (6.1)

Возможно существуют и другие варианты представления аргумента функции, но в этой работе рассматривается этот вариант.

Здесь происходит дифференцирование суммы функции и её аргумента, уже показанное правило, следующее из одномерной системы координат (3.2):

. (6.2)

т. к. в начальном случае аргумент и функция равны. Аргумент становится сложной функцией.

Второе интегрирование здесь не имеет смысла, т. к. аргумент вычитается из функции, и это говорит о том, что в одномерной системе координат на первом этаже существует только один путь интегрирования, второй путь появится на втором этаже функциигде происходит это вычитание.

В декартовой системе координат, где дифференцируется только функция производная получает коэффициент — ½. Этот коэффициент в одномерной системе координат, следовательно, опускается, т. к. функция и аргумент суммируются.

Обозначим соответствующие аргументы через переменные:

, . (6.3)

и условные дифференциалы сингулярного пространства (исходя из условия (3.3)):

, . (6.4)

Ортонормированные составляющие функции симметричны относительно единицы, такое условие обеспечивает выражение составляющих функции через оператор -. Возможно, что существуют и другие варианты представления функции, по здесь рассматривается только этот вариант.

Поскольку функция имеет этажную структуру, то она может быть представлена составляющими.

Общий вид составляющих получает выражение:и , которым соответствуют интегралы на первом этаже, имеющие определённый вид:

. (6.5)

Каждый интеграл отвечает за свой полупериод колебательного процесса. Выражение (6.5) удовлетворяет условию (4.2).

В динамическом процессе после первого интегрирования происходит переход ко второму: , после чего происходит обратный переход . Этим обеспечивается их последовательность и симметричность относительно центра осцилляции, являющегося и центром интегральной симметрии.

Принципиального отличия в приоритете пространств нет, но если уже приоритет сделан, то в дальнейшем следует ему придерживаться поскольку этим выбрано положительное направление интегрирования.

Кроме уже рассмотренной функции первого этажа (6.5) условию (4.2) удовлетворяют также функции (с удвоением степени под радикальных переменных), соответствующие последующим — этажам , которые можно назвать этажными составляющими — функции. Эти интегралы можно привести к виду:

(6.6)

, ,

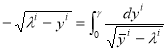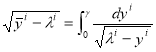где - этаж системы.

Такой вид интегралов, показывающий стадии развития колебательной системы со степенным характером осцилляторов не показывает её структуры. Раскрытие дифференциалов позволяет её прочитать. Дифференциалы — функции требуют отдельного рассмотрения.

7 Дифференциалы -функции

Дифференциалы -функции приводятся для определения пути интегрирования и структуры колебательной системы.

Развитие колебательной системы (с учётом её этажной структуры) выражается появлением нового осциллятора, для внедрения которого требуется новый дифференциал на каждом последующем этаже.

Для сохранения симметричности системы необходимо со стороны дополнитьсо стороны :

, . (7.1)

Здесь дифференциал имеет вполне конкретное объяснение: система координат с плавающей точкой отсчёта имеет девиацию центра осцилляции, следящей за процессом и имеющей сингулярный характер. Из этого положения получены дифференциалы — этажей:

, . (7.2)

После подстановки дифференциалов интегралы (6.6) получают совершенный вид:

(7.3)

,

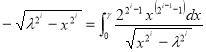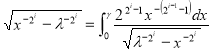
Отношение двух сопряжённых дифференциалов: - показывает степень ортонормированности в зависимости от этажа. Эта величина показывает - центр осцилляции двух ортонормированных составляющих функции, и должна быть учтена в значениях - функции, т. к. вносит свой вклад в процесс осцилляции, что и будет сделано в дальнейшем.

8 Составляющие -функции

Следуя представленным уравнениям (7,4) выражения и (здесь для упрощение записи принимается ) можно разложить на отдельные составляющие - функции, и могут быть представлены в общем виде:

, . (8.1)

Составляющие - функции и в общем виде описываются уравнениями:

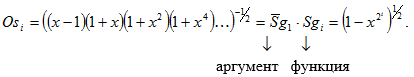(8.2)

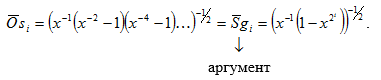(8.3)

Это выражение можно записать так, что выявится факт поглощения аргумента первой составляющей:

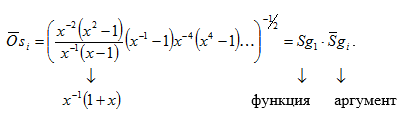(8.4)

Для получения выражений (8.2) и (8.3) использовано тождество :

, . (8.5)

Первая составляющая является аргументами - функции. В одномерной системе координат значение аргумента вместе со значением функции входит в полное значение составляющей.

9 Нахождение значений -функции

В пространствах значения аргумента, как и самой функции, принимают дискретные значения. Каждый интеграл в (7.4) имеет только одно значение функции, отвечающее своему этажу.

Для первого этажа показаны значения интегралов с верхним пределом интегрирования , т. к. является окружением для пространства и наоборот, что и определяет пределы интегрирования :

, . (9.1)

Функция не имеет смысла во втором выражении, т. к. в одномерной системе координат аргумент функции, равный самой функции, из этой же функции вычитается. Выражение (9.1) подтверждает положения (6.3) и (3.2). Осцилляция на этом этаже невозможна, и на эта составляющая далее не рассматривается, но возможность имеет на более высоких этажах.

Далее, системапереходит на новый этаж, где определяется приоритет или для дальнейшего рассмотрения, в данном случае — к .

Для пространства в пределы интегрирования входит значение аргумента и значение функции.

Для пространства в пределы интегрирования входят значения функции без значения аргумента. Эти значения приведены в (9.2) :

(9.2)

, ,

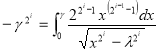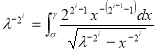где нижний предел второго интеграла — .

Таким образом, имеется два числовых дискретных массива: и , представляющие значения - функции.

10 Два дискретных числовых массива - функции

- функции принадлежат дискретные значения, определяемые из (9.2). Эти значения сведены в табл. 10.1, где расставлены в соответствии со структурой колебательных систем (т. е. поэтажно) применительно к и пространствам.

пространство учитывается как прямое, - как обратное, и наоборот. Для приведения их в функциональное равенство ведомые составляющие (или) умножаются на поправку - (см. (7.5)).

Таблица

Значения составляющих

Этими двумя числовыми массивами описываются все ортонормированные колебательные системы, составленные из осцилляторов. Каждая из составляющих «играет свою роль» в структуре колебательной системы, что делает её уникальной на каждом этапе эволюции.

11 Вывод

В работе получены значения - функции в пространстве, описывающие этажную структуру динамической системы с одной степенью свободы. Осциллирующий процесс в систем обеспечивают и осцилляторы, в ортонормированной системе координат с плавающим центром осцилляции, что принципиально отличается от декартовой системы координат . Этот центр следует за осцилляцией сингулярной системы относительно дифференциального центра колебаний — , т. к. в пространствах геометрический центр колебаний не определён.

Функция принимает только дискретные числовые значения, промежутки между этими значениями являются сингулярными.

Поскольку иосцилляторы ортонормированы, то система координат не имеет нулевой точки отсчёта. Нулевое значение в такой системе координат означает отсутствие объекта исследования.

- функция состоит из двух числовых массивов, кратных значению . Она не имеет нулевого значения, т. к. нулевое значение дискретной функции означает её отрицание, также, как и отсутствие колебательной системы в целом.

На каждом - этаже система представлена своим осциллятором, отмеченным постоянным числовым значением, систему можно рассматривать как абстрактный объект с — этажной структурой.

После нормировки система может быть характеризована как физический объект, что позволяет эффективное её использование в различных приложениях. Например, в приложениях эти два числовых массива могут описывать квантовые системы, т. е. описывать как элементарные частицы, так и соответственно античастицы (в зависимости от приоритета ). Для этого и вводится в этой работе понятия пространства и - функции.

Литература:

1. Мигулин В. В., Медведев В. И., Мустель Е. Р., Парыгин В. Н. Основы теории колебаний. 2 изд. — М.: Наука, 1988. — 391 с.
2. А. M. Севастьянов. Сингулярное пространство АТТ «Виртуальный мир». 2, 2016.
3. Riley, K. F.; Hobson, M. P.; Bence, S. J. Mathematical methods for physics and engineering. New York: Cambridge University Press (2002). “Chapter 19”.
4. Bakshi K. A. Electronic Measurement Systems. — US: Technical Publications, 2008. — P. 4 -14.
5. Ли Софус Симметрии дифференциальных уравнений. Лекции о дифференциальных уравнениях с известными инфинитезимальными преобразованиями. Том 1. Серия: Математика и механика. Издательство «РХД» 2011 г. 704 с.
6. Яблонский А. И., Кузнецов А. В., Шилкина Е. И. и др. Высшая математика. Общий курс: Учебник / Под общ. ред. С. А. Самаля. — Мн.: Выш. шк., 2000. — 351 с.
7. Bailey, D. H. and Crandall, R. E. Random Generators and Normal Numbers. Exper. Math. 11, 527–546, 2002.
8. Cajori F. A history of mathematical notations, v. 1–2, Chi., 1928–29.