Получены аналитические выражения, позволяющие определить асимптотическую дисперсию оптимальной оценки временнόго положения (задержки) импульсного радиосигнала в виде отклика одиночного колебательного контура на прямоугольный радиоимпульс. Показано, что использование уточненной формулы, определяющей дисперсию оценки при не очень большом отношении сигнал-шум, в случае рассматриваемого сигнала невозможно.
Ключевые слова: измерение задержки сигнала, оптимальный прием, согласованный фильтр, дисперсия ошибки, нормальный белый шум
При анализе характеристик устройств приема и обработки радиосигналов в качестве теоретической модели сигнала часто используется колебание в виде отклика одиночного колебательного контура на радиоимпульс с прямоугольной огибающей, действующий на резонансной частоте контура. Для измерения временнόго положения такого сигнала, имеющего случайную начальную фазу и принимаемого на фоне нормального белого шума, применяются оптимальные устройства обработки на основе согласованного фильтра [1]. При этом временнόе положение сигнала определяется относительно некоторого начального момента времени, т. е. измеряемым параметром является задержка 
. При действии шума точность измерения задержки сигнала характеризуется дисперсией. Теоретическая (минимально достижимая) дисперсия ошибки измерения задержки определяется выражением [1, стр.190, (3.3.38)]
, (1)
где 
— среднеквадратическая ширина спектра сигнала, 
– максимальное отношение сигнал-шум на выходе согласованного фильтра, равное
.
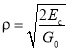Здесь 
– энергия сигнала, 
— спектральная плотность шума.
Поскольку радиоимпульс является узкополосным сигналом, то среднеквадратическая ширина его спектра определяется относительно центральной частоты. Следовательно, для рассматриваемого сигнала она равна ширине спектра колебания на выходе низкочастотного эквивалента колебательного контура при воздействии на него прямоугольного видеоимпульса. Среднеквадратическая ширина такого колебания выражается через значение второй производной его нормированной автокорреляционной функции (АКФ) в нуле:
. (2)
Известно [2], что низкочастотным эквивалентом одиночного колебательного контура является инерционное звено (интегрирующая RC-цепь). Импульсная характеристика интегрирующей цепи с постоянной времени Tопределяется выражением [2]
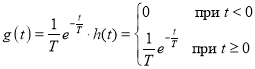,(3)
где 
— функция Хевисайда (функция единичного скачка).
Вычислим АКФ сигнала 
на выходе низкочастотного эквивалента
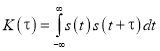. (4)
Отклик интегрирующей цепи равен свертке прямоугольного импульса и импульсной характеристики цепи 
:
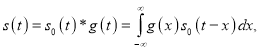(5)
где 
— сигнал в видепрямоугольного импульса длительности 
. Амплитуду импульса будем считать равной 1. График сигнала 
при 
, 
и 
показан на рис. 1.
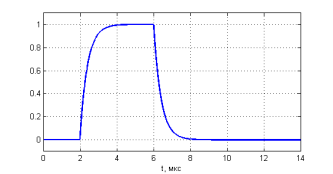
Рис. 1. Импульс на выходе интегрирующей цепи
Подставляя (5) в (4), получим
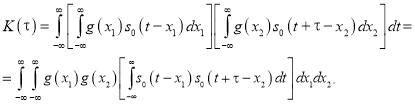
Выражение в квадратных скобках связано с АКФ прямоугольного импульса 
следующим соотношением:
.
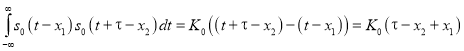Вторая производная АКФ сигнала равна
.
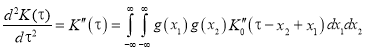Следовательно, ее значение в нуле определяется выражением
.
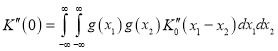АКФ прямоугольного импульса равна
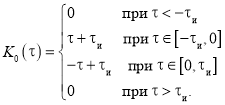
Ее график имеет вид треугольника с основанием от 
до 
и высотой . Поэтому вторая производная равна
, (6)
где
— δ-функция.
Подставляя (6) в выражение для 
, получим
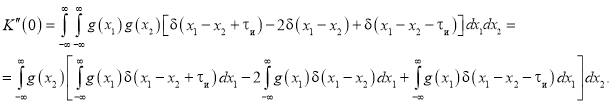Вычисляя внутренние интегралы с учетом «фильтрующего» свойства δ-функции, получаем выражение для значения второй производной АКФ в нуле в виде суммы трех интегралов:
.
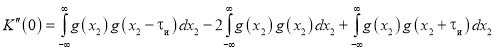Подставляя в это выражение импульсную характеристику интегрирующей цепи (3) и вычисляя каждый из интегралов, получим:
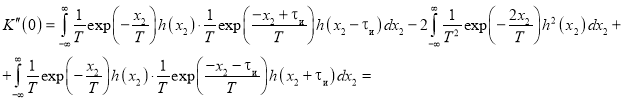
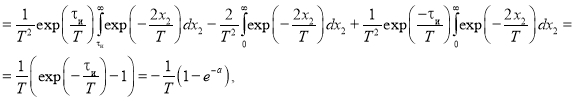
где 
— параметр, характеризующий степень прямоугольности импульса.
Для нормировки полученное выражение для второй производной АКФ сигнала в нуле нужно разделить на значение АКФ сигнала в нуле 
, которое равно энергии сигнала
.
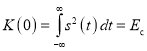Сигнал, который является реакцией интегрирующей цепи на прямоугольный импульс единичной амплитуды, описывается выражением [2]
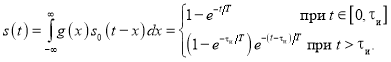
Вычислим энергию сигнала:
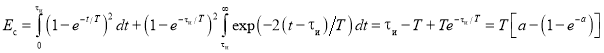
Тогда нормированная вторая производная АКФ сигнала в нуле равна
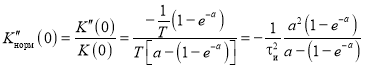
и в соответствии с (2) среднеквадратическая ширина спектра сигнала определяется выражением
.
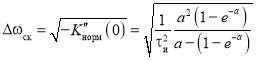Подставляя ее в выражение для дисперсии ошибки измерения задержки (1), получаем
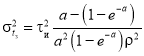. (7)
Формула (1), на основании которой получено выражение (7), выводится при условии, что ошибка измерения имеет нормальный закон распределения вероятностей. Она является асимптотической и определяет только минимально возможную дисперсию ошибки. Поэтому рассмотрим также формулу, приведенную в [3, стр.76, 3.1.48], которая учитывает отклонение распределения вероятностей ошибки от нормального и может дать более точный результат при не очень больших значениях отношения сигнал-шум. В этой формуле учитывается дополнительная поправка к дисперсии, вычисленной в соответствии с (1):
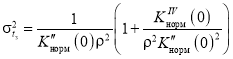. (8)
Для определения поправки вычислим значение четвертной производной АКФ сигнала в нуле 
. Для этого в формулу, определяющую вторую производную АКФ сигнала, подставим выражение (6) для второй производной АКФ прямоугольного импульса и результат запишем как сумму трех слагаемых:
,
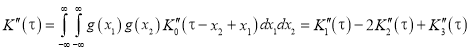где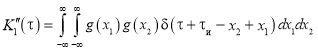 
,
,
.
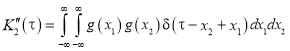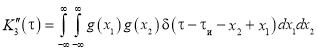Выражения для 
и 
отличаются от 
только тем, что в параметр 
входит со знаком «минус», а в он равен нулю. Поэтому достаточно получить формулу только для .
.
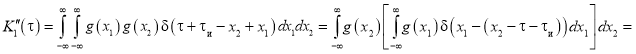
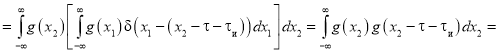
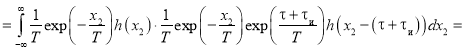
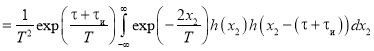Для того чтобы дальше преобразовать это выражение, нужно отдельно рассмотреть два случая.
1) 
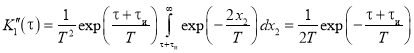
2) 
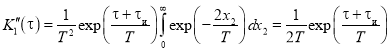
Объединяя эти два выражения, окончательно получим:
.
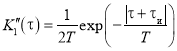Выражение для 
получается, если в этой формуле положить 
:
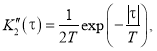
а выражение для 
— если изменить знак у 
:
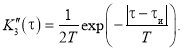
Таким образом, окончательно получаем
.
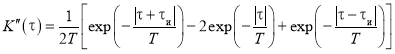График АКФ сигнала показан на рис. 2, а график ее второй производной — на рис. 3.
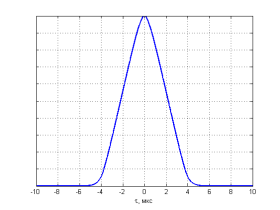
Рис. 2. График АКФ сигнала
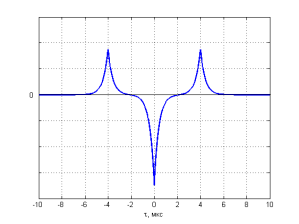
Рис. 3. График второй производной АКФ
График второй производной АКФ 
имеет излом в нуле. Следовательно, третья производная (рис. 4) в нуле имеет разрыв, а четвертая производная не существует (является бесконечно большой).
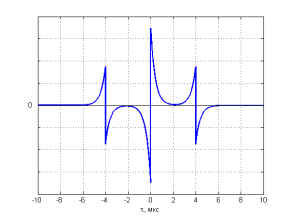
Рис. 4. График третьей производной АКФ
Таким образом, для рассматриваемого сигнала нет возможности определить дисперсию ошибки с поправкой по формуле (8). Поэтому необходимо искать другие способы повышения точности расчета дисперсии ошибки измерения задержки при не очень большом отношении сигнал-шум, в том числе основанные на имитационном моделировании.
Литература:
1. Тихонов В.И. Оптимальный приём сигналов. — М.: Радио и связь, 1983.
2. Баскаков С.И. Радиотехнические цепи и сигналы. — 3-е изд. — М.: Высшая школа, 2000.
3. Куликов Е.И., Трифонов А.П. Оценка параметров сигнала на фоне помех. — М.: Советское радио, 1978.
