Предложен подход к калибровке микро-опто-электро-механического (МОЭМ) датчика угловых скоростей на основе оптического туннельного эффекта (ОТЭ), обоснован многопозиционным методом, позволяющим определить калибровочные коэффициенты и нулевые смещения измерения. Изложен алгоритм обработки выходных сигналов методом фильтрации Кальмана для уменьшения измерительных шумов.
Ключевые слова: калибровка, нулевое смещение, фильтрация Кальмана, МОЭМ, угловая скорость.
Approach to calibration of the micro-opto-electro-mechanical (MOEM) sensor based on optical tunnelling effect (OTE) is proposed, by using multiposition method that allowing for the determination of measurement calibration coefficient and zero-bias. The output signals processing algorithm by using Kalman filtering method for measuring noise reduction is represented.
Keywords: calibration, zero-bias, Kalman filtering, MOEM, angular velocity.
Калибровка представляет собой процесс устранения большей части систематической погрешности прибора путём определения коэффициентов коррекции, согласованных при формировании выходные сигналы по всему диапазону выходных сигналов [1–2]. Существуют многие методики калибровки приборов, зависящие от принципов работы, способа определения измеряемой и самой величины измерения [3–7].
Cтруктура МОЭМ-датчика угловых скоростей на основе ОТЭ, состоящая из основного канала приемо-передачи оптического излучения, включающего оптического разветвителя, связанная световодами с источником излучения и фотоприемниками, соединенным электрически с блоком обработки информации и оптически, через световод, с системой модуляции «оптического узла — воздуха — чувствительного пьезоэлемента» [3]. При этом, предлагается подход к калибровке данного датчика, включающий в себя: способ определения калибровочных масштабных коэффициентов и вектора нулевых смещений, и алгоритм обработки выходных сигналов с применением фильтра Калмана [6–7].
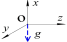
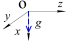
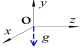
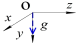
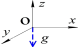
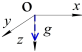
Способ определения калибровочных масштабных коэффициентов и вектора нулевых смещений. Предположим, что связанная система координат OXYZ ориентирована относительно неподвижной системы OX g Y g Z g по углам θ X , θ Y , θ Z . описаны матрицы перехода для поворота вокруг OX, OY, OZ оси на угол θ X , θ Y , θ Z от связанной системы координат OXYZ к системе координат OX g Y g Z g :
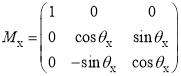
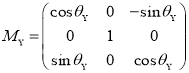
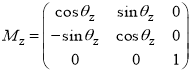
Следовательно, получена общая матрица перехода М Р от связанной системы координат OXYZ к неподвижной OX g Y g Z g :
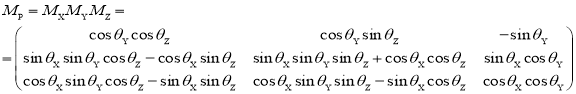
Квазилинейная функция МОЭМ-датчика угловых скоростей на основе ОТЭ с учетом нулевого смещения В 0 = [ В 0 X , В 0 Y , В 0 Z ] T и случайного шума измерения Ξ Ω = [ X Ξ Ω , Y Ξ Ω , Z Ξ Ω ] T может быть переписана в виде:
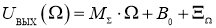
где М ∑ — суммарная матрица коэффициентов:
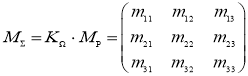
K Ω =diag [ K X Ω , K Y Ω , K Z Ω ] — диагональная матрица масштабных коэффициентов исследуемого датчика.
Для оценки вышеуказанных параметров, как матриц масштабных коэффициентов, так и вектора смещений нуля предлагается методика, реализованная на основе способа многопозиционной калибровки [6–7]. Принцип этой способа калибровки заключается в выполнении эксперимента с достаточными положениями ориентации МОЭМ-датчика угловых скоростей на основе ОТЭ в пространстве, необходимыми для оценки параметров с требуемой точностью (табл. 1) [6].
Таблица 1
|
Положения |
Оси O x |
Оси O y |
Оси O z |
Иллюстрация положения |
|
1 |
1 |
0 |
0 |
|
|
2 |
-1 |
0 |
0 |
|
|
3 |
0 |
1 |
0 |
|
|
4 |
0 |
-1 |
0 |
|
|
5 |
0 |
0 |
1 |
|
|
6 |
0 |
0 |
-1 |
|
Предположим, три оси чувствительности МОЭМ-датчика угловых скоростей были размещены на трехосную поворотную платформу. Для получения калибровочных коэффициентов ошибок при регулировании трехосной поворотной платформы с одинаковым значением угловой скорости (Ω 0 ≠ 0) по шести оптимальным положениям 1 .. 6 (табл. 1) определены и усреднены выходные данные трехосевого датчика.
Исходя из полученных результатов для шести оптимальных положений 1 .. 6 система уравнения (2) может переписать в виде:
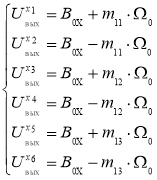
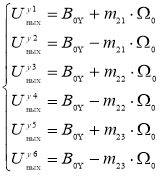

Таким образом, калибровочные масштабные коэффициенты и нулевые смещения МОЭМ-датчика угловых скоростей определяются по следующим формулам:
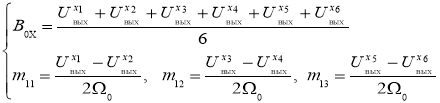
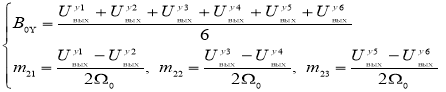
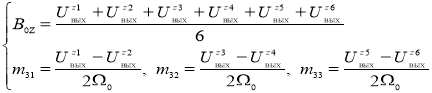
Отметим, что доверенность результатов определения матрицы калибровочных масштабных коэффициентов и вектора смещений нуля прибора целесообразно зависит от точности при выполнении экспериментов и также точности установки на трехосной поворотной платформе.
Алгоритм обработки выходных сигналов. Внастоящее время обработка измеряемых сигналов в МЭМС-приборах осуществляется современными цифровыми микро-ЭВМ и процессорами, позволяющими реализовать методы и алгоритмы обработки на основе матричных операций в режиме реального времени, что существенно повышает эффективность измерительных систем [7–9]. Выделение измеряемой величины из сигналов при наличии шумов часто выполняется с применением фильтрации Калмана — последовательного рекурсивного алгоритма, основанного на квадратичном критерии качества, т. е. обеспечивает минимум среднеквадратических ошибок измерительных данных [9–10].
В общем случае модель измерения МОЭМ-датчика угловых скоростей может быть выражена следующим образом:
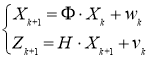
где X k — вектор переменных состояния в момент времени k , Z k — вектор выходных сигналов системы (измеряемые) в момент времени k , Φ — матрица перехода состояния системы, Н — матрица измерения, w k , v k — векторы шумов системы и ошибок измерения в момент времени k соответственно.
Предполагая, что шумы системы и измерения
w
k
и
v
k
считаются независимыми случайными процессами по Гауссовскому закону распределения с нулевым математическим ожиданием и ковариационными матрицами:
Q
,
R
— для шума системы и измерения соответственно. Процедура фильтрации Калмана осуществляется по двум этапам «предсказание — корректировка». Допустим, что в момент времени
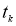
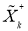
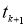
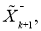
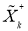
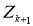
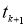
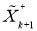
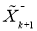
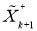
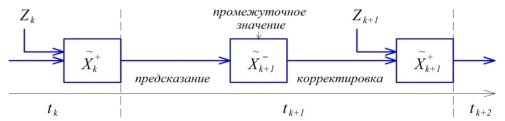
Рис. 1. Иллюстрация процедуры фильтрации Калмана


единичная матрица с соответствующей размерностью.
Заданные начальные условия X 0 – и P 0 – существенно влияют на быстродействие фильтрации Калмана и тем точнее предсказанные знания о процессе и шумах системы, тем выше быстродействие процесса фильтрации Калмана [8–10]. В соответствии с типичными положениями калибровки, модели измерения датчика по трем осям могут быть записаны в виде [6–7]:
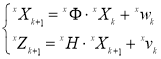
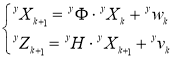
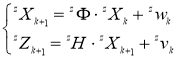
где x X= [ x B Ω m 11 m 12 m 13 ] T , y X= [ y B Ω m 21 m 22 m 23 ] T , z X= [ z B Ω m 31 m 32 m 33 ] T ,
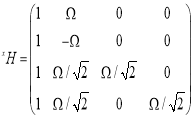
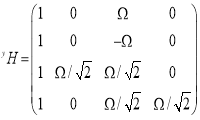
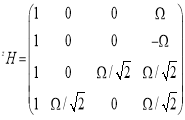
Выводы. Теоретически изложен подход к калибровке МОЭМ датчика угловых скоростей на основе ОТЭ, обоснованный многопозиционным методом с некоторыми упрощенными. При этом, определены калибровочные коэффициенты и нулевые смещения измерения по шести оптимальным положениям. И также описан алгоритм обработки выходных сигналов методом фильтрации Кальмана, позволяющий уменьшить измерительные шумы. Для полной реализации калибровки таких приборов, включая связанные с ними оценки неопределенности, нелинейные явления в МОЭМ системах (флуктуация интенсивности самого оптического сигнала от источника излучения до фотоприемников, флуктуации интенсивности, обусловленные воздействием на систему внешней среды, также искажение выходных сигналов при обработке и. т.д.), необходимы учитывать как факторы, влияющие на действительные значения их параметров.
Литература:
- Дмитриев С. А., Слепов Н. Н. Волоконно-оптическая техника: современное состояние и новые перспективы. — М.: Техносфера, 2010. — 608с.
- Bin F., Wusheng C., Li D. An optimal calibration method for MEMS inertial measurement unit // International Journal of Advanced Robotic Systems. 2014. Vol.11. — p. 1–14.
- Бусурин В. И., Фам А. Т., Жеглов М. А., Медведев В. М. Трехосевой микро-опто-электро-механический преобразователь угловых скоростей на основе оптического туннельного эффекта // Автометрия, 2017, Т. 53, № 6, — с. 33–41.
- Козлов С. И. Использование инфракрасных приборов в космической технике и дальнейшие перспективы их развития // Вестник науки и образования, 2019. №. 3–2(57), — с. 10–15.
- Штерцер Н. А., Выборнов Н. А. Датчики для измерения мощности на выходе передающего каскада радиопередатчика и коэффициента стоячей волны в антенно-фидерном устройстве // Вестник науки и образования, 2019. №. 8–1(62), — с. 26–30.
- Холопов И. С. Калибровка цифровых трехосных MEMS акселерометров по шести ортогональным положениям скоростей // Радиотехнические и телекоммуникационные системы. 2015, № 2. –с. 61–65.
- Yu L. et al. Calibration of MEMS Accelerometer based on Kalman filter and improved six position method // Journal of Communications. 2016. Vol. 11, iss. 5. — p. 516–521.
- Стегнеев С. В., Панкова К. В. Анализ перспективных отечественных фотоприемников на основе гетероструктур А3В5 // Вестник науки и образования, 2018. №. 3 (39), — с. 29–31.
- Прокофьева П. Е., Лапшин И. Г., Пахомов А. М. Новый метод и прибор по определению чистоты нефтехимии с применением обратного пьезоэлектрического эффекта // Вестник науки и образования, 2018. №. 15–1(51), — с. 16–19.
- Димов Ю. В. Метрология, стандартизация и качество. 3-е издание. Издательский дом «Питер», 2010–463 с.