В работе рассмотрена устойчивость осесимметричных форм равновесия однородных изотропных пластин, моделирующих решетчатую пластинку диска зрительного нерва человека. В предположении, что несимметричная составляющая решения носит периодический характер, численным методом определено наименьшее значение нагрузки, при которой появляются волны в окружном направлении. Исследовано влияние различных условий закрепления пластины, наличия и размеров отверстия в центре пластины на величину критической нагрузки и форму потери устойчивости.
Ключевые слова: биомеханика глаза, круглая пластина, потеря устойчивости.
Введение. В данной работе была рассмотрена задача о потере устойчивости симметричной формы равновесия однородной круглой пластины. Такая пластина может быть простейшей моделью решетчатой пластины диска зрительного нерва человека [6]. Были поставлены две задачи: исследовать влияние условий закрепления края на величину критической нагрузки; рассмотреть задачу о возникновении неосесимметричных состояний у кольцевой пластины.
Впервые вопрос о существовании несимметричных решений у симметрично загруженной круглой пластины был рассмотрен в [1]. Исследуя большие прогибы пластины, загруженной постоянным давлением, авторы получают решение, соответствующее несимметричным формам равновесия.
Строгое доказательство существования несимметричного решения для симметрично нагруженной пластины было проведено в [2], а его единственность доказана в работе [3].
В работах [4], [5] для пологой сферической оболочки и круглой пластины при различных условияx закрепления и нагружения определены значения критической нагрузки, при которой происходит переход от симметричной формы равновесия к неосесимметричной.
Постановка задачи. Рассмотрим круглую изотропную пластину, защемленную по краю и находящуюся под действием равномерно распределенного давления. Запишем систему уравнений в виде [7]:
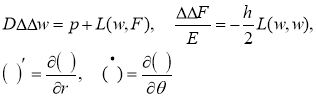
где w(r, θ) , F(r, θ) — неизвестные функция нормального прогиба и функция усилий; D = Eh 3 / 12(1-ν 2 ) — цилиндрическая жесткость пластины, E — модуль упругости пластины, R — радиус пластины, h — толщина пластины, ν — коэффициент Пуассона материала пластины, p — нормальное давление, действующее на пластину; r и θ — полярные координаты срединной поверхности пластины: 0 ≤ r ≤ R , 0 ≤ θ ≤ 2 π ; оператор Лапласа Δ и дифференциальный оператор L имеют вид:
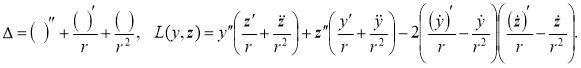
Функция
F(r,θ)
связана с возникающими при деформации усилиями в пластине, по следующим формулам [7]:
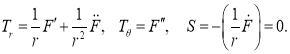
Предположим, что точки края r = R закреплены от поворотов, но свободно смещаются в радиальном и окружном направлениях. В этом случае растягивающее ( T r ) и сдвигающее ( S ) усилия на контуре полагаем равными 0:
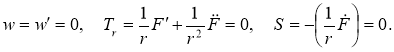
Введем безразмерные переменные
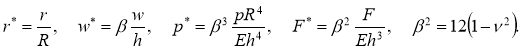
Тогда система уравнений (1) примет следующий вид (знак * в дальнейшем опускаем):

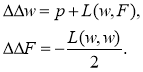
Граничные условия сохраняют вид (2).
Для сплошной пластины граничные условия (2) должны быть дополнены условиями ограниченности решений в центре
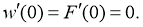
Метод поиска несимметричного решения. Нам нужно найти критическое значение нагрузки p = p cr , при котором возможна бифуркация пластины в неосесимметричное состояние. При значениях нагрузки p меньше критического значения система (3), дополненная необходимыми граничными условиями, имеет только симметричное решение. Несимметричное решение этой системы появляется при возрастании нагрузки.
Будем искать решение в виде
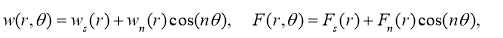
где функции w s , F s описывают докритическое симметричное решение, а функции w ns (r, θ) = w n (r) cos(nθ) , F ns (r, θ) = F n (r) cos(nθ) — закритическое состояние пластины (здесь n — число волн в окружном направлении, образовавшихся после потери устойчивости).
После разделения переменных (4) исходная система (1)–(2) распадается на нелинейную для нахождения симметричного решения w s (r) , F s (r) и линейную относительно w n (r) , F n (r) , так как функции w ns , F ns полагаются малыми сразу после перехода пластины в неосесимметричное состояние.
Подставляя (4) в (3), с учетом обозначений
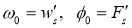
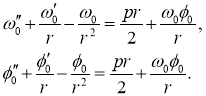
Граничные условия (2) с учетом ограниченности решений в центре пластины примут вид
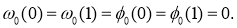
Для несимметричного решения после разделения переменных получим линейную систему уравнений относительно w n (r) и F n (r)
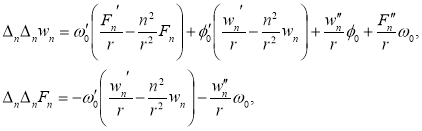
где
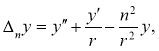
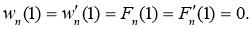
Учитывая ограниченность искомых решений, в центре пластины полагаем
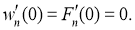
Для каждого числа волн n будем искать такие значения нагрузки p n , при которых существуют отличное от нуля решение системы (7)-(9) при условии (5)-(6). Под критической нагрузкой p cr будем понимать наименьшее значение нагрузки p n , т. е. p cr = min n (p n ).
Схема численного решения задачи состоит из двух этапов и аналогична методу, описанному в работах [4], [5]. На первом этапе решается симметричная задача (5)-(6). Для заданных p и n вычисляются w s , F s и их производные. Затем с помощью метода конечных разностей проверяется существование решения несимметричной задачи.
Пластина с упруго-заделанным краем . Нелинейная задача теории пластин и оболочек допускает различные варианты граничных условий на краю пластины. Рассмотрим случай наличия по краю пластины упругой связи (пружины), препятствующей ее свободному смещению в радиальном направлении, тогда проекция вектора перемещения u на ось r и тангенциальное усилие T r на внешнем крае взаимосвязаны, т. е. k u u + T r = 0, где k u — коэффициент упругости заделки.
Таким образом, система уравнений (1) сохраняется, а граничные условия запишутся в виде
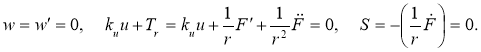
Чтобы выразить компоненту перемещения u(r, θ) через искомые функции w , F , воспользуемся представлением компонент деформации ε r , ε θ , ω через компоненты вектора перемещения u , v , w, с одной стороны, и усилий T r , T θ , S , с другой:
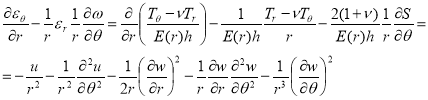
После разделения переменных (4) граничные условия для симметричной задачи (5) запишутся в виде
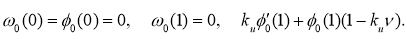
Для системы (7), описывающей несимметричное решение, граничные условия примут вид
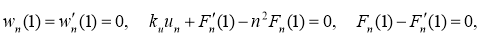
где
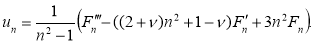
Случай кольцевой пластины . В случае кольцевой пластины вместо условий ограниченности решений в центре пластины необходимо задать граничные условия. Одним из возможных вариантов закрепления внутреннего края ( r = δ ) может быть свободное перемещение точек края в радиальном и окружном направлении при ограничении поворотов. Тогда необходимо принять равным нулю поперечное реактивное усилие, складывающееся из поперечной силы и производной от крутящего момента. В терминах нормального перемещения w и функции усилий F граничные условия запишутся в следующем виде:
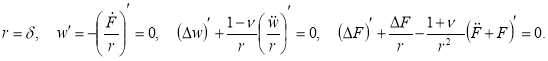
На внешнем крае пластины r = 1 в общем случае можно задать условия упругой заделки (10). Тогда система уравнений, описывающая симметричное равновесное состояние, примет вид
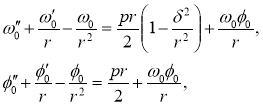
с граничными условиями
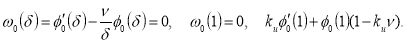
Результаты. Были проведены серии расчетов для находящейся под давлением однородной пластины, а также для пластины с упруго-заделанным краем, для кольцевой пластины и для пластины, совмещающей эти свойства.
Для однородной сплошной пластины с краем, который может свободно смещаться в радиальном направлении, наименьшее критическое значение нагрузки p cr 0 и соответствующее ему волновое число n , найденные в результате решения системы (7)-(8), оказались равны p cr 0 = 67236 и n = 13. Полученные результаты для n = 10, 11, …, 20 представлены в таблице 1.
Таблица 1
Значения критических нагрузок и соответствующих волновых чисел для однородной сплошной пластины.
|
n |
10 |
11 |
12 |
13 |
14 |
15 |
|
p cr |
114751 |
77425 |
69387 |
67236 |
67587 |
69335 |
|
n |
16 |
17 |
18 |
19 |
20 | |
|
p cr |
71998 |
75331 |
79197 |
83512 |
88223 |
В случае упругой связи по краю пластины, с ростом жесткости пружины k u пластина переходит в неосесимметричное состояние при более высоких величинах критической нагрузки и с образованием большего числа волн в окружном направлении, что можно увидеть в таблице 2. В таблице 3 представлены минимальные критические нагрузки для рассмотренных k u .
Таблица 2
Значения критических нагрузок и соответствующих волновых чисел для однородной сплошной пластины с упруго-заделанным краем.
|
k u n |
0.001 |
0.01 |
0.05 |
0.1 |
0.15 |
0.2 |
0.3 |
|
10 |
170170 | ||||||
|
11 |
80908 |
94485 | |||||
|
12 |
69107 |
77457 |
139087 | ||||
|
13 |
65527 |
72240 |
115036 |
241263 | |||
|
14 |
65088 |
71111 |
106897 |
191116 |
420604 | ||
|
15 |
66296 |
72026 |
104650 |
173081 |
315936 |
748190 | |
|
16 |
68538 |
74184 |
105413 |
166377 |
277496 |
524978 | |
|
17 |
71514 |
77205 |
108021 |
165256 |
261119 |
444182 | |
|
18 |
75058 |
80883 |
111909 |
167447 |
255179 |
407551 | |
|
19 |
79074 |
85098 |
116770 |
171866 |
255211 |
390838 |
1177638 |
|
20 |
83501 |
89776 |
122424 |
177927 |
259124 |
385084 |
1007669 |
Таблица 3
Минимальные значения критических нагрузок и соответствующих волновых чисел для однородной сплошной пластины с упруго-заделанным краем
|
k u |
0.001 |
0.01 |
0.05 |
0.1 |
0.15 |
0.2 |
0.3 |
|
n |
14 |
14 |
15 |
17 |
18 |
20 |
24 |
|
p cr 0 |
65088 |
71111 |
104650 |
165256 |
255179 |
385084 |
839714 |
Значения критических нагрузок и соответствующих им волновых чисел, полученных в результате вычислений для кольцевой пластины при различных значениях радиуса отверстия δ , показаны в таблице 4. Наименьшие значения нагрузки для каждого δ представлены в таблице 5.
Таблица 4
Значения критических нагрузок и соответствующих волновых чисел для однородной кольцевой пластины
|
δ n |
0.01 |
0.05 |
0.1 |
0.15 |
0.2 |
|
10 |
132711 |
100303 |
87653 |
84136 |
85533 |
|
11 |
78075 |
74328 |
73353 |
75429 |
80280 |
|
12 |
67938 |
67746 |
69631 |
73746 |
80285 |
|
13 |
64952 |
66238 |
69583 |
74971 |
82766 |
|
14 |
64827 |
67024 |
71400 |
77817 |
86740 |
|
15 |
66242 |
69133 |
74378 |
81740 |
91765 |
|
16 |
68639 |
72133 |
78183 |
86470 |
97613 |
|
17 |
71743 |
75800 |
82636 |
91857 |
104156 |
|
18 |
75401 |
80006 |
87633 |
97815 |
111317 |
|
19 |
79521 |
84676 |
93111 |
104286 |
119048 |
|
20 |
84047 |
89761 |
99027 |
111238 |
127318 |
Таблица 5
Минимальные значения критических нагрузок и соответствующих волновых чисел для однородной кольцевой пластины.
|
δ |
0.01 |
0.05 |
0.1 |
0.15 |
0.2 |
|
n |
14 |
13 |
13 |
12 |
11 |
|
p cr 0 |
64827 |
66238 |
69583 |
73746 |
80280 |
В случае наличия у кольцевой пластины упруго-заделанного края, так же, как и в случае сплошной пластины, при увеличении жесткости пружины k u переход в неосесимметричное состояние происходит при более больших значениях критической нагрузки и с образованием большего числа волн. Результаты расчетов можно увидеть в таблице 6. В таблице 7 показаны наименьшие критические значения нагрузки и соответствующие им волновые числа для каждого рассмотренного δ и k u = 0.001, 0.01, 0.05.
Таблица 6
Значения критических нагрузок и соответствующих волновых чисел для кольцевой пластины с упруго-заделанным краем
|
k u n |
0.001 |
0.01 |
0.05 |
0.001 |
0.01 |
0.05 |
|
δ = 0.01 |
δ = 0.0 5 | |||||
|
10 |
187592 |
108171 | ||||
|
11 |
80840 |
76321 |
115819 | |||
|
12 |
69235 |
88269 |
68813 |
83346 | ||
|
13 |
65769 |
76222 |
66944 |
75778 | ||
|
14 |
65409 |
72546 |
67536 |
73822 | ||
|
15 |
66680 |
72050 |
69521 |
74342 | ||
|
16 |
68978 |
73228 |
72430 |
76274 | ||
|
17 |
72005 |
75459 |
149816 |
76024 |
79143 |
137269 |
|
18 |
75599 |
78436 |
127516 |
80167 |
82704 |
126009 |
|
19 |
79663 |
81988 |
120868 |
84780 |
86817 |
122550 |
|
20 |
84136 |
86013 |
119003 |
89809 |
91397 |
122395 |
|
δ = 0. 1 |
δ = 0. 15 | |||||
|
10 |
91445 |
86641 |
154917 | |||
|
11 |
74842 |
97850 |
76640 |
93552 | ||
|
12 |
70514 |
81970 |
74512 |
84222 | ||
|
13 |
70191 |
77731 |
75510 |
82227 | ||
|
14 |
71846 |
77397 |
78211 |
83253 | ||
|
15 |
74713 |
79029 |
82028 |
85959 | ||
|
16 |
78433 |
81874 |
154570 |
86672 |
89773 |
149685 |
|
17 |
82813 |
85574 |
134873 |
91984 |
94408 |
139630 |
|
18 |
87746 |
89935 |
129286 |
97870 |
99704 |
137238 |
|
19 |
93161 |
94843 |
128379 |
104273 |
105564 |
138238 |
|
20 |
99017 |
100227 |
129883 |
111156 |
111927 |
141206 |
|
δ = 0. 2 | ||||||
|
10 |
87448 |
120305 | ||||
|
11 |
81323 |
95204 | ||||
|
12 |
80970 |
89635 | ||||
|
13 |
83250 |
89427 | ||||
|
14 |
87086 |
91755 | ||||
|
15 |
92003 |
95611 |
177220 | |||
|
16 |
97760 |
100533 |
155426 | |||
|
17 |
104220 |
106282 |
149991 | |||
|
18 |
111300 |
112720 |
149921 | |||
|
19 |
118951 |
119761 |
152622 | |||
|
20 |
127138 |
127351 |
157069 | |||
Таблица 7
Минимальные значения критических нагрузок и соответствующих волновых чисел для кольцевой пластины с упруго-заделанным краем
|
k u δ |
0.001 |
0.01 |
0.05 | |||
|
n |
p cr 0 |
n |
p cr 0 |
n |
p cr 0 | |
|
0.01 |
14 |
65409 |
15 |
72050 |
20 |
119003 |
|
0.05 |
13 |
66944 |
14 |
73822 |
20 |
122395 |
|
0.1 |
13 |
70191 |
14 |
77397 |
19 |
128379 |
|
0.15 |
12 |
74512 |
13 |
82227 |
18 |
137238 |
|
0.2 |
12 |
80970 |
13 |
89427 |
18 |
149921 |
Для k u = 0.1, 0.2, 0.3, рассмотренных в случае сплошной пластины, значения критических нагрузок оказываются очень большими при большом числе образующихся волн. Пример для случая k u = 0.1 приведен в таблице 8.
Таблица 8
Минимальные значения критических нагрузок и соответствующих волновых чисел для кольцевой пластины с упруго-заделанным краем при k u = 0.1
|
δ |
0.01 |
0.05 |
0.1 |
0.15 |
0.2 |
|
n |
31 |
30 |
29 |
29 |
28 |
|
p cr 0 |
1165458 |
1153910 |
1190263 |
1444323 |
1488912 |
Заключение. В данной работе представлены результаты численного исследования потери устойчивости осесимметричных форм равновесия однородных сплошных и кольцевых пластин при различных условиях закрепления внешнего края.
Показано, что при увеличении жесткости пружины, ограничивающей перемещение края пластины в радиальном направлении, как в случае сплошной, так и в случае кольцевой пластины переход в неосесимметричное состояние происходит при значительно больших критических нагрузках и с образованием большего числа волн в окружном направлении. Показана зависимость значений критической нагрузки от размеров отверстия в центре в случае кольцевой пластины.
Литература:
- Панов Д. Ю., Феодосьев В. И. О равновесии и потере устойчивости пологих оболочек при больших прогибах // ПММ. Т.XII. 1948. С. 389–406.
- Морозов Н. Ф. К вопросу о существовании несимметричного решения в задаче о больших прогибах круглой пластины, загруженной симметричной нагрузкой // Изв. Высш. Уч. Заведений. Математика. 1961. № 2. С. 126–129.
- Piechocki W. On the non-linear theory of thin elastic spherical shells // Arch. Mech. Stos. 1969. N21. P. 81–101.
- Huang N. C. Unsymmetrical buckling of thin shallow spherical shells // J. Appl. Mech. 1964. N31. P. 447–457.
- Cheo L. S., Reiss E. L. Unsymmetric wrinkling of circular plates // Quart. Appl. Math. 1971. N31. P. 75–91.
- Bauer S. M., Voronkova E. B. On the deformation of the Lamina Cribrosa under intraocular pressure // Russian Journal of Biomechanics. 2001. Vol. 5. N1. P. 73–82.
- Бауэр С. М., Воронкова Е. Б. О потере устойчивости симметричных форм равновесия круглых пластин под действием нормального давления // Вестн. С.-Петерб. ун-та. Сер. 1. 2012. Вып. 1. С. 80–85.

