В статье предложены формулы для определения депрессии, связанной с увеличением скорости фильтрации и наличием влияния начального градиента и который должен быть дополнительно преодолен. Получен аналитический вид для его определения, который позволяет количественно оценить влияние инерционных сил и начального градиента на дебит скважин.
Ключевые слова: градиент, давление, депрессия, фильтрация.
The article proposes formulas for determining the depression associated with an increase in the filtration rate and the presence of the influence of the initial gradient and which must be further overcome. An analytical view was obtained for its determination, which allows one to quantify the influence of inertial forces and the initial gradient on the well flow rate.
Keywords: gradient, pressure, depression, filtration.
При разработке залежей с аномальными свойствами нефтей возникает ряд сложных и специфических задач, связанных с изучением физических и гидродинамических задач, связанных с изучением физических и гидродинамических основ проявления неньютоновского характера фильтрации в пористой среде. [1–4.]
В свете этих задач важное значение приобретают методы количественной интерпретации результатов гидродинамических исследований пластов и скважин, являющихся, по-видимому, основным надежным источником получения достоверной информации о величине начального перепада давления и о других исходных данных, необходимых для проектирования разработки месторождения с аномальными свойствами углеводородов.
В данной работе усовершенствована методика интерпретации кривых при влиянии начального градиента и инерционных сил на процесс фильтрации. С учетом влияния начального градиента и двучленного закона Форхгеймера, закон фильтрации имеет следующий вид:
при 
(1)
при 
.
Решая это уравнение, получаем для дебита углеводородов выражение в виде:
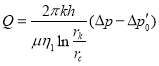, (2)
где 
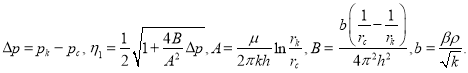
(3)
А теперь покажем, как получается формула для 
.
Как известно, для дебита нефти при двучленном законе фильтрации существует выражение 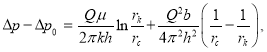[4]:
(4)
Левую часть в формуле обозначим через 
, и коэффициент при Q и Q2 обозначим соответственно через А и В. Тогда получается выражение в виде:
(5)
Проведем следующие преобразования:
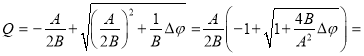
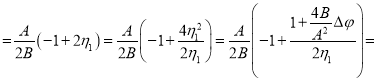
(6)
Здесь Последнее является искомым выражением.
Таким образом, можно используя формулу 
, найти зависимость 
(рис. 1, 2).
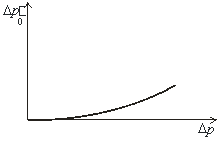
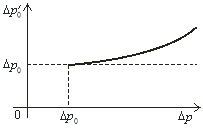
Рис. 1. Рис. 2.
График изменения 
от График изменения от
Как видно, во время фильтрации флюида в пористой среде при наличии начального градиента и при влиянии инерционных сил, полученная депрессия, направленная против движения, увеличивается.
Литература:
- Гасанов И. Р., Таирова С. А., Гасанов Р. И. Изучение особенностей проявления неньютоновских свойств углеводородов в процессе разработки и исследования методом установившихся отборов // Молодой ученый: Международный научный журнал. –Казань. — № 22, 2016. —С. 24- 28.
- Гасанов И. Р., Таирова С. А., Гасанов Р. И. Методика интерпретации индикаторных линий скважин, добывающих углеводороды с аномальными свойствами // Научно-технический вестник: Каротажник. – Тверь. — № 1, 2017. –С. 62–68.
- Гасанов И. Р., Таирова С. А., Гасанов Р. И. Прогнозирование коэффициента продуктивности залежей углеводородов с аномальными свойствами и по данным гидродинамических исследований скважин при установившихся режимах // Молодой ученый: Международный научный журнал. –Казань. — № 26, 2016. –С. 24–28.
- К. С. Басниев, А. М. Власов, И. Н. Кочина, В. М. Максимов. Подземная гидравлика. — М.: Недра, 1986. — 303 с.
