Рассмотрим кубатурную формулу вида

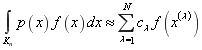(1)

над пространством Соболева , где — -мерный единичный куб.

Обобщённая функция

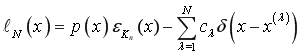(2)

называется функционалом погрешности кубатурной формулы (1),

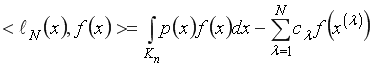
является погрешностью кубатурной формулы (1), весовая функция, — характеристическая функция , и — коэффициенты и узлы кубатурной формулы (1) и — дельта-функция Дирака.

Определение. Пространство — определяется как пространство функций заданных на -мерном единичном кубе и имеющие все обобщённые производные порядка , суммируемые со степенью в норме (см. [1])

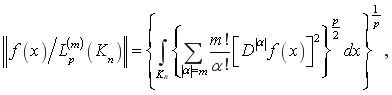(3)

где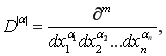

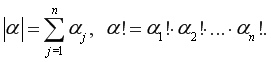
Справедлива следующая

Лемма. Если для функционала погрешности (2) кубатурной формулы (1) выполняется условие Декартовых произведений, т. е.

и

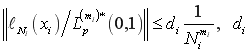- константы,(4)

т. е.

- константы, ,(5)

то

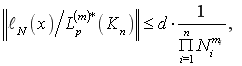
- константа,(6)

или

,

где 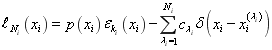, и .

С помощью этой леммы легко доказывается следующая теорема.

Теорема. Весовая кубатурная формула (1) с функционалом погрешности (2) пр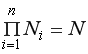и и является оптимальной по порядку сходимости над пространством т. е. для нормы функционала погрешности (2) кубатурной формулы (1) имеет место равенство

.

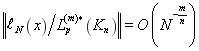Доказательство.

На основе леммы при имеем , .

Итак,

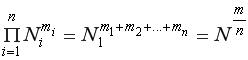.(7)

Подставляя (7) в неравенство

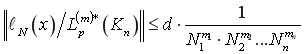
получим

,(8)

Из теоремы Н. С. Бахвалова [3] и неравенство (8) следует доказательство сформулированной теоремы.

Литература:

1. Соболев С. Л. Введение в теорию кубатурных формул. — М.: Наука, 1974–808с.
2. Соболев С. Л. Некоторые применения функционального анализа в математической физике. Л.: Наука. 1988, — 333с.
3. Бахвалов Н. С. С Оценки снизу асимптотических характеристик классов функций с доминирующей смешанной производной, Мат. заметки, 1972, т.2. № 6, -С.655–664.