В статье рассматривается одно из прикладных применений метода блочно-функционального распределения в качестве синтаксического анализатора для вычисления значений алгебраических выражений.
Успех внедрения информационно-измерительных систем, информационно-вычислительных комплексов, автоматизированных систем управления технологическими процессами в различные сферы жизни зависит не только от требований заказчика, но и от того, насколько данные требования учтены и реализованы в необходимом объеме. Для того, чтобы учесть все требования заказчика, необходима детальная проработка этих сведений как для проектирования данного объекта с учетом реализованных функций, так и с учётом требований среды, в которой будет функционировать объект. Детальная проработка этих требований достигается только с позиций структурно-иерархического системного подхода. Этот подход представляет собой математический аппарат, на основании которого возможно, детализируя алгоритм БФР путём проработки под конкретные случаи, разработать многочисленные алгоритмы процедур и функций как основу для построения специализированных программных систем (ПС). Проектируемая структура отображается в виде направленного графа, где вершины — подсистемы, стойки, блоки, платы, дискретные элементы — это зависит от уровня детализации по структурно-иерархическому представлению, а рёбра — информационные связующие функциональных элементов. Согласно алгоритму блочно-функционального распределения (БФР) [1, 3], нулевой уровень детализации это граф — состоящий из одной единственной вершины с описанием свёртки входящих и выходящих информационных составляющих. Первый уровень детализации — это уровень подсистем (в случае, если при проектировании используется модель предметов). Вершины графа первого уровня детализации в этом случае — это подсистемы. Свертка входящих и выходящих информационных составляющих в этом случае распределяется на все подсистемы, представленные вершинами. Каждая вершина подсистемы может быть детализирована направленным графом стойки и т. д. Детализация ведётся до тех пор, пока обнаружится принципиальная схема, образующая тот или иной функциональный элемент.
Изначально алгоритм блочно-функционального распределения [1, 2] было принято использовать для оптимального размещения функций по элементам определённого уровня с целью сохранения функциональности всей проектируемой ИИС. Этот алгоритм может работать как и для синтеза (с использованием оптимизации структуры по критерию наименьшей/наибольшей внешней устойчивости), так и для анализа (например, построение синтаксического анализатора, позволяющего из функции, заданной алгебраически построить её структурное представление в виде направленного графа. Это производится путём выделения отдельных функциональных элементов, сопоставления выделенного функционального элемента с элементарным фрагментом, добавления фрагмента в массив данных получаемой структуры и вывод полученной структуры на контекст отображения. Таков алгоритм реализован [3].
Целесообразно вместо структурных фрагментов использовать фрагменты элементарных или составных математических выражений, представленные в виде строк. Затем вместо строковых аргументов поставить реальные числа и вычислить значение, результат преобразовать в строковое представление и подставить на место фрагмента выражения. В виде блок схемы это будет выглядеть как на рисунке 1.
Проиллюстрируем работу этого алгоритма на примере вычисления выражения
0,7*x^3+x^2–3*x-67 для значения x=0,349.
П.1;Ш.1 Подставляем вместо x числовое значение: '0,7*0,349^3+0,349^2–3*0,349–67'. (1)
П.1;Ш.2 Инициализируем строковый массив операторов ('+', '-', '*', '/', '+', '-', '*', '/', 'sin', 'cos', 'ctg', 'tg', 'cosec', 'sec', 'log', 'ln', 'lg', '^') и фрагментов выражений ('(?+?)', '(?-?)', '(?*?)', '(?/?)', '?+?', '?-?', '?*?', '?/?', 'sin(?)', 'cos(?)', 'ctg(?)', 'tg(?)', 'cosec(?)', 'sec(?)', 'log(?)(?)', 'ln(?)', 'lg(?)', '?^?'). (2)
П.1;Ш.3 Заменяем знак отрицательного числа на @1*: '0,7*x^3+x^2+@1*3*x+@1*67'. (3)
П.1;Ш.4 Выделяем из выражения числовые и буквенные составляющие с занесением в отдельный строковый массив ('0,7', 'x', '3', 'x', '2', '@1', '3', 'x', '@1', '67'). (4)
П.1;Ш.5 Формируем на основе исходной строки строку без числовых и буквенных составляющих, заменяя последние вопросительными знаками: '?*?^?+?^?+?*?*?+?*?'. (5)
П.1;Ш.6 Формируем массив порядковых номеров этих вопросительных знаков: (1, 3, 5, 7, 9, 11, 13, 15, 17, 19). (6)
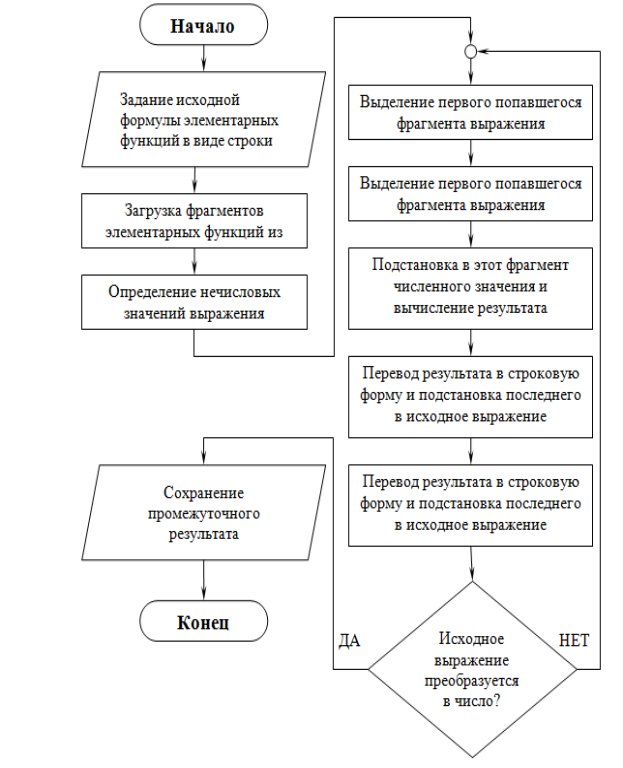
Рис. 1. Блок-схема
П.1;Ш.7 Выделение первого фрагмента выражения и оператора:?^? и ^. (7)
П.1;Ш.8 Подстановка вместо? численных значений: '0,349^3'. (8)
П.1;Ш.9 Определение начала выражения (8) в выражении (3). (9)
П.1;Ш.10 Вычисление значения (8)вчисленном виде:0,042508549. (10)
П.1;Ш.11 Преобразование результата из (10)встроку и подстановка в (3)вместо '0,349^3': '0,7*0,042508549+0,349^2+@1*3*0,349+@1*67'. (11)
П.1;Ш.12 Проверка выражения из (11)на число. Оно числом не является.
Начинается второй проход с шагами 3–11.
П.2;Ш.3 Заменяем знак отрицательного числа на @1*: '0,7*0,042508549+0,349^2+@1*3*0,349+@1*67'. (3)
П.2;Ш.4 Выделяем из выражения числовые и буквенные составляющие с занесением в отдельный строковый массив ('0,7', '0,042508549', '0,349', '2', '@1', '3', '0,349', '@1', '67'). (4)
П.2;Ш.5 Формируем на основе исходной строки строку без числовых и буквенных составляющих, заменяя последние вопросительными знаками: '?*?+?^?+?*?*?+?*?'. (5)
П.2;Ш.6 Формируем массив порядковых номеров этих вопросительных знаков: (1, 3, 5, 7, 9, 11, 13, 15, 17). (6)
П.2;Ш.7 Выделение первого фрагмента выражения и оператора:?^? и ^. (7)
П.2;Ш.8 Подстановка вместо? численных значений: '0,349^2'. (8)
П.2;Ш.9 Определение начала выражения (8) в выражении (3). (9)
П.2;Ш.10 Вычисление значения (8)вчисленном виде:0,121801. (10)
П.2;Ш.11 Преобразование результата из (10)встроку и подстановка в (3)вместо '0,349^2': '0,7*0,042508549+0,121801+@1*3*0,349+@1*67' (11)
П.2;Ш.12 Проверка выражения из (11)на число. Оно числом не является.
Начинается третий проход с шагами 3–12.
Для того, чтобы получить результат вычисления — окончательное число, '@67,8954430157' для данного выражения потребовалось 9 проходов данного алгоритма. Нормальный результат — -67,8954430157.
Как показывает пример применения БФР к анализу и вычислению аналогового выражения, аналогичный подход можно использовать и для логических выражений, если заменить список элементарных компонент.
Литература:
- Муха, Ю.П., Алгебраическая теория синтеза сложных систем [Текст] / Ю. П. Муха, О. А. Авдеюк, И. Ю. Королёва. — Волгоград: Изд-во Политехник, 2003. — 320 с.
- Математические методы информатики в задачах и примерах: Опыт применения в проектировании сложных систем: учеб. пособие [Текст] / Авдеюк О. А., Горбачев С. В., Муха Ю. П., Секачев В. А., Сырямкин В. И.,Титов В. С., Ширабакина Т. А.; ФГБОУ ВПО «Национальный исследовательский Томский гос. ун-т».-Томск: Изд-во Томского ун-та, 2012. — 483 с.
- Синтезатор структур измерительных систем из функционального уравнения: свидетельство об официальной регистрации программы для ЭВМ. ВНТИЦ № 2007613258 Российская Федерация / Муха Ю. П., Секачёв В. А.; зарегистрировано в реестре программ для ЭВМ 03.08.2007.
- Рубичев, Н.А., Измерительные информационные системы [Текст] / Н. А. Рубичев. — М: Дрофа, 2010. — 334, [2] с.: ил.
- Новиков, Ф. А. Дискретная математика для программистов [Текст] / Ф. А. Новиков. — СПб.: Изд-во Питер, 2001. — 304 с.

