В этой статье описывается метод последовательных приближений для решения обыкновенных дифференциальных уравнений.

Дифференциальные уравнения, имеют широкое применение в физике, в механике, в дифференциальной геометрии, в вариационной исчисление, в химии, в биологии, в электротехнике, в экономике и в других сферах науки.

Многие процессы описываются при помощи дифференциальных уравнений. Эти дифференциальные уравнения являются математической моделью данного процесса. Характеризуя математику как метод проникновения в тайны природы, можно сказать, что основным путем применения этого метода является формирование и изучение математических моделей реального мира. Изучая какие-либо физические явления, исследователь, прежде всего создает его математическую идеализацию или, другими словами, математическую модель, то есть, пренебрегая второстепенными характеристиками явления, он записывает основные законы, управляющие этим явлением, в математической форме. Очень часто эти законы можно выразить в виде дифференциальных уравнений.

Определение 1. Дифференциальным уравнением называется уравнение, связывающее искомую функцию некоторой переменной, эту переменную и производную и производные различных порядков данной функции:

Если неизвестная функция в дифференциальном уравнении является функцией от одной переменной, тогда это уравнения называется обыкновенным дифференциальным уравнением. Если неизвестная функция в дифференциальном уравнении является функцией от многих переменных, тогда это уравнения называется дифференциальным уравнением в частных производных.

В частном случае мы рассмотрим обыкновенное дифференциальное уравнение первого порядка, который имеет следующий вид:

Если это уравнение можно представить в следующем виде:

(1)

тогда это уравнения называется дифференциальным уравнением разрешенное относительно производной.

Определение 2([1]). Пусть задано уравнение (1) и функция определена в области Г плоскости R². Если для функции определенной на интервале I выполняются следующие условия

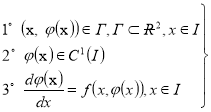(2)

Тогда эта функция на интервале I называется решением (1) дифференциального уравнения. Решение, заданного в неявном виде, называется интегралом дифференциального уравнения.

График решения (интеграла) дифференциального уравнения называется интегральной кривой.

Пусть задано уравнение (1) и функция определена, непрерывна в области Г плоскости R² и интервал является интервалом на оси , которому принадлежит точка . Требуется найти такую функцию определенной на интервале I, для которой выполняются следующие условия

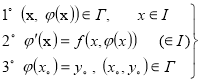` (3)

Эта задача записывается следующим образом: и называется задачей Коши для (1) уравнения.

Задачу Коши, поставленную для любого дифференциального уравнения нельзя решать аналитически.

Из теоремы существование и единственности решения задачи Коши дифференциального уравнения, для метода последовательности можно получать следующие формулы:

Применение этой формулы посмотрим в одном примере,

Пример.

Точное решение этого уравнения:

Решение 3-го приближения следующее:

Нарисуем графики этих решений, т. е. точное и приближенное решение при помощи программы Mathcad:

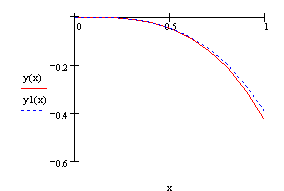
Из графика решений можно видеть, что этот метод мы можем применять для уравнений неинтегрируемых на квадратурах.

Литература:

1. Салохиддинов М. С., Насриддинов Г. Н. Оддий дифференциал тенгламалар. Тошкент, Ўзбекистон”, 1994 й.
2. Н. Ш. Кремер. Высшая математика для экономистов. Москва, Юнити, 2007 г.
3. Филиппов А. Ф. Сборник задач по дифференциальным уравнениям. М. наука, 1979 (5 –е издание).