В этом работе дается описание единичных шаров конечномерных нейтральных сильно гранево симметричных пространств малых размерностей.
Исследования гранево симметричных пространств связаны с геометрической характеризацией предсопряженных пространств JBW*-троек, допускающих алгебраическую структуру, и восходят к работам Я.Фридмана и Б.Руссо [1]. Аксиомы, требуемые в этих характеризациях, являются естественными предположениями для пространств состояний физических систем. Такие пространства рассматриваются как геометрические модели для состояний квантовой механики. Естественно, что предсопряженные пространства для комплексных алгебр фон Неймана и более общих JBW*-троек являются нейтральными сильно гранево симметричными пространствами [2].
В работе [3] были даны геометрическая характеризация комплексных гильбертовых пространств и комплексных спин-факторов, а также дано описание JBW*-троек ранга 1 и 2, факторов Картана типа 1 и 4. М. Нейл и Б.Руссо в [4] нашли геометрические условия, при которых гранево симметричное пространство является изометричным предсопряженному пространству JBW*-тройки. Условие, при котором слабо гранево симметричное пространство является сильно гранево симметричным пространством, было найдено Н.Ядгоровым в [5].
Сначала приведем необходимые сведения о гранево симметричных пространствах.
Пусть
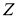
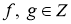
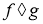
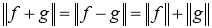
Грань
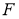
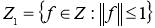
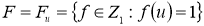
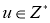
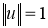
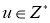
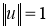
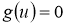
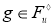
Выставленная по норме грань
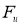
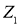
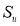
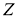
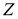
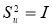
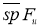
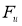
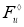
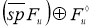
Пространство
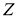
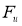
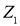
Для каждой симметричной грани
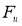
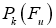
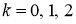
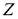
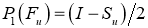
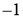
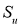
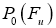
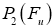
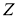
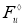
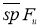
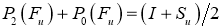
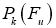
Проективная единица
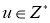
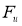
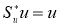
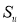
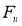
WFS-пространство
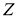
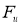
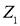
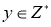
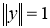
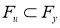
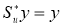
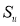
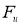
Сжимающий проектор
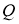
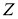
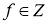
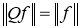
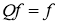
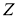
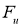
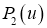
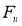
Определение
[3]
.
Сильно гранево симметричное пространство
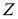
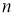
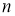
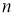
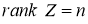
Имеет место следующие теорема.
Теорема 1.
Пусть
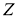
1) Если
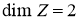
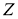
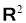
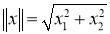
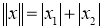
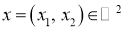
2) Если
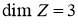
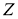
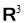
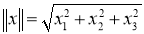
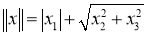
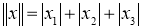
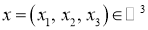
Следующая теорема, дает описание единичных шаров четырехмерных нейтральных сильно гранево симметричных пространств.
Теорема 2.
Пусть
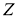
1) Если
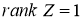
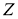
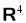
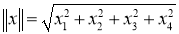
2) Если
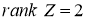
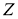
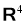
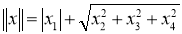
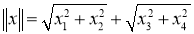
3) Если
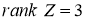
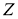
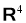
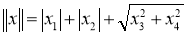
4) Если
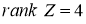
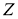
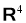
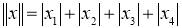
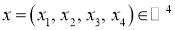
Геометрический трипотент
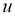
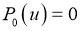
Обозначим
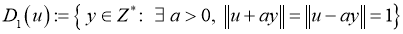
Имеет место следующая
Теорема 3.
Пусть
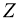
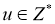
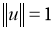
1)
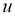
2)
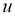
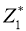
3)
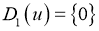
Литература:
- Friedman Y., Russo B. Affine structure of facially symmetric spaces // Math. Proc. Camb. Philos. Soc. Vol. 106. 1989. № 1. P. 107–124.
- Friedman Y., Russo B. Some affine geometric aspects of operator algebras // Pac. J. Math. Vol. 137. 1989. № 1. P. 123–144.
- Friedman Y. and Russo B. Geometry of the dual ball of the spin factor // Proc. Lon. Math. Soc. 1992. Vol. 65. № 3. P. 142–174.
- Neal M., Russo B. State space of JB * -triples // Math. Ann. 2004. Vol. 328. № 4. P. 585–624.
- Ядгоров Н. Ж. Слабо и сильно гранево симметричные пространства // Докл. АН РУз. 1996. № 5. с. 6–8.
- https://cyberleninka.ru/article/n/geometricheskaya-harakterizatsiya-veschestvennyh-jbw-faktorov

