В статье представлен анализ геометрической фигуры с последующем синтезированием их, как комплексный чертеж модели в трех плоскостям 
проекции. Показано, на конкретном примере, построение на одной модели комплексные формы геометрических фигур.
Ключевые слова: окружность, метод, горизонталь, фронталь, профиль, ось, координата, проекция, плоскость, построение, модель, призма, пирамида, цилиндр, конус, сопряжение, классификация, вид, форма, фигура.
В статьях [1, 2] приводится метод построения двух и более геометрических фигур модели в трех плоскостях 
, 
и 
проекции. Мы расширяем в глубь данный метод с построением на них комплексные формы геометрических фигур. Основа модели берется окружность круга и строится вокруг нее вписанный и описанный многогранники.
Путем анализа определяем конкретный вид геометрической фигуры и синтезируем их, как комплексный вид чертежа модели в трех плоскостях. Например, окружность в горизонтальной плоскости проекции выглядит как круг, а в других вертикальной и профильной плоскости проекциях смотрится как цилиндр или конус. Также многогранник (трех и т. д.) может выглядеть призмой, если задать с вершиной, то как пирамида. Помимо этого, по виду поверхности формы геометрические фигуры классифицируются на: выпуклые и вогнутые тела, т. е. геометрические фигуры имеют комбинированные или комплексные виды формы. На рисунке 1 приводится цилиндр и призмы с выпуклой I и вогнутой II поверхностью. Все эти геометрические фигуры имеют полые тела, т. е. тела со сквозными отверстиями.
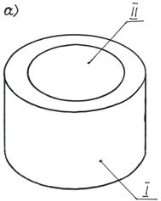
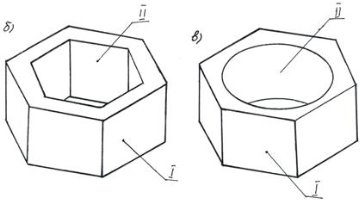
Рис. 1. Фигуры, имеющие выпуклую I и вогнутую II поверхность тела.
Для любого многогранника справедлива формула Эйлера, устанавливающая связь между числом вершин 
, ребер 
и граней 
:
, (1)
здесь число 
называется Эйлеровой характеристикой и может равняться 
Также Эйлеровая характеристика 
показывает сколько отверстий 
может иметь по центру осевой линии многогранник:
(2)
или 
Например, для шестигранной монолитной призмы число, которой равны 
; 
и 
, то подставляя их в уравнение (1), получим 
. Полученное число по Эйлеровской характеристике показывает, что призма имеет выпуклую поверхность. Для комбинированной (комплексной) поверхности призмы (рисунок 1, б), который имеет выпуклую и вогнутую поверхность, тогда число вершин, ребер и граней будут равны 
, 
. Подставляя их в уравнение (1), получим 
, отсюда полученный результат по Эйлеровской характеристике показывает, что сама плоскость поверхности над вогнутой поверхности призмы отсутствует. Для установления призмы сквозного отверстия воспользуемся формулой (2), для этого подставляя численные значения, получим 
. Это показывает, что внутри призмы по осевой линии можно иметь только одно сквозное отверстие (рисунок 1, б и в).
Шестигранная призма может иметь комплексный вид данной формы, что наглядно видно на рисунке 1, б и в. Поэтому для получения комплексного геометрического модели, мы с учетом компоновки чертежа на формате А3 строим круг диаметром Ø
и в центре горизонтальной плоскости по координатной оси 
проводим по ним две пересекающие осевые линии, обозначая ее точкой 
(рисунок 2, а). По приведенной методике [1] делим окружность на шесть частей. Краткое графическое построение дано на рисунке 2, а: длина отрезка 
дает сторону правильного шестиугольника вписанных в окружность круга с центром . По фиксированным точкам 
соединяя их контурными линиями — получаем вписанный в окружность шестигранник. Второй описанный по окружности шестигранник строится также по вышеприведенному методу, для этого определяем высоту 
хорды 
и на расстоянии 
проводим касательные линии и получаем описанный по окружности круга второй шестигранник 
(рисунок 2, б). Окружность является сопряженной частью соприкосновения в точках линии круга обоих многогранников.
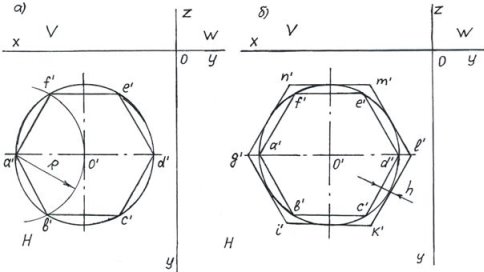
Рис. 2. Графический способ построения на основе круга окружности шестигранников
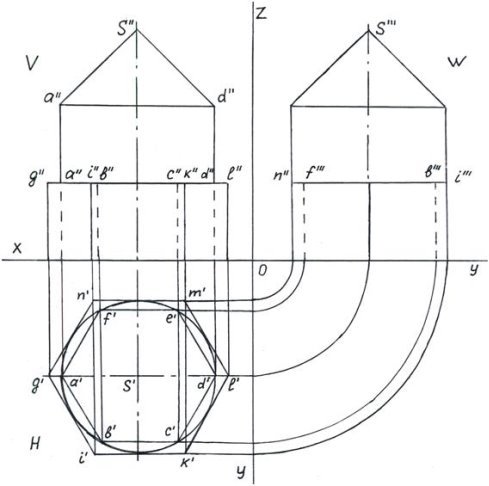
Рис. 3. Построение комплексных фигур на одной модели
По полученным контурным проекциям модели устанавливаем вид геометрических фигур. Так круг окружности радиусом 
с центром является сечением поверхности горизонтальной плоскости цилиндра (рисунок 2, а и б).
Вписанный шестигранник 
является контуром призмы с вогнутой II формы поверхности данной призмы (рисунок 2, б), а второй описанный шестигранник 
имеет выпуклую I форму. Поэтому призма имеет полый вид (рисунок 1, б). Также круг окружности с вершиной является основанием конуса, а высотой его является точка 
(рисунок 3, плоскость ). Из горизонтальной 
плоскости проекции (рисунок 3) проводим ортогональные линии точки призмы и на фронтальную плоскость проекции.
Фиксируем их на координатной оси 
выпуклую форму часть призмы 
, а также на высоте координатной оси 
верхнюю и нижнюю части вогнутую форму призмы 
, при этом на данную высоту 
проецируем с горизонтальной плоскости проекцию круга окружности и фиксируем их точками 
а на уровне 
по оси 
верхнюю часть также точками 
. Эти точки являются верхней частью цилиндра 
, а также нижним основанием конуса и на высоте , 
и фиксируем верхушки конуса точкой 
. Проецируя их из горизонтальной плоскости во фронтальные 
и профильные плоскости проекции фиксируемые все точки модели с высотой по 
для каждой фигуры (рисунок 2, плоскости и ): мы получаем комплексный чертеж модели из трех фигур призмы, цилиндра, и конуса.
Из выше приведенного можно сделать следующие выводы и предложения:
студенты должны ясно представлять смысл и содержание слов, графических терминов, при построениях геометрических фигур;
при построении пятиугольника надо разделить окружность на 6 частей и построить вписанный в круг окружности шестиугольник, а также описанный по окружности круга шестиугольник;
обучить студентов методике сравнения полученных фигур по габаритным параметрам, при построении вписанной и описанной по окружности полученных шестиугольников.
Литература:
- Алимов Б. М., Пулатова Х. А. Метод построения двух геометрических фигур на одной модели. // Молодой ученый. — 2014. № 9 (68). — С. 98–101.
- Алимов Б. М., Уразкелдиев А. Б. Построение трех и более геометрических фигур на одной модели. // Молодой ученый. — 2015. № 10 (90). — С. 1077–1080.
