В статье рассмотрен метод построения уравнения касательной кривой в параметрическом виде, для дорожки прямого вращения при движении сателлита ременной передачи планетарного механизма аппарата хлопкоуборочной машины.
Ключевые слова: ролик, шпиндель, ремень, касательная, передача, машина, привод, реверс, угол, уравнение, эволюта, кривая, скольжение.
В аппарате хлопкоуборочной машины [1] привод шпинделей осуществляется при помощи фрикционной передачи, т. е. при помощи ремней прямого и обратного вращения. Наряду с положительными свойствами имеются и недостатки: так по всей длине ременной передачи происходит неравномерный износ, т. е. в зоне реверса ролика шпинделя происходит интенсивный износ ремней за счет перемены вращения сателлита в обратную сторону ударной нагрузки при входе ролика в ремни прямого вращения. Также уменьшает срок службы опор верхних и нижних подшипников и, а также и вследствие чего увеличивается скольжение роликов по ремням прямого и обратного вращения происходит пробуксовка приводного ролика шпинделей хлопкоуборочной машины.
Целью работы является усовершенствование конструкции механизма за счет повышение плавности захода шпинделей приводным ремнем путем применения каркаса, который имеет профиль дуги по касательной кривой и имеет по заданной форме эволюту.
На рисунке 1 показан привод шпинделей, который состоит из дорожки 1 ремни прямого вращения и колодки 2 обратного вращения, длина дуги которых равна ![]() — рабочему углу сбора хлопка-сырца шпинделем 3 уборочного аппарата и
— рабочему углу сбора хлопка-сырца шпинделем 3 уборочного аппарата и ![]() углу в зоне съема хлопка-сырца со шпинделя. Обычно ремень, при натянутом положении образует ломанную линию (рисунок 1) и в точках перегиба происходит большое давление пружин на приводной ролик 3 шпинделя. При вращении барабана с угловой скоростью
углу в зоне съема хлопка-сырца со шпинделя. Обычно ремень, при натянутом положении образует ломанную линию (рисунок 1) и в точках перегиба происходит большое давление пружин на приводной ролик 3 шпинделя. При вращении барабана с угловой скоростью ![]() (рисунок 1) приводной ролик 3 набегают на ремень 1 прямого вращения, следовательно, точка перегиба постоянно меняется. Максимальная длина ломанной линии (от жестко закрепленного 4 конца до ролика А) — ОА. Тогда точка В — момент соприкосновения (точка касания) ролика по ремню прямого вращения, то в этом момент получается удар по касательной линии с силой
(рисунок 1) приводной ролик 3 набегают на ремень 1 прямого вращения, следовательно, точка перегиба постоянно меняется. Максимальная длина ломанной линии (от жестко закрепленного 4 конца до ролика А) — ОА. Тогда точка В — момент соприкосновения (точка касания) ролика по ремню прямого вращения, то в этом момент получается удар по касательной линии с силой ![]() .
.
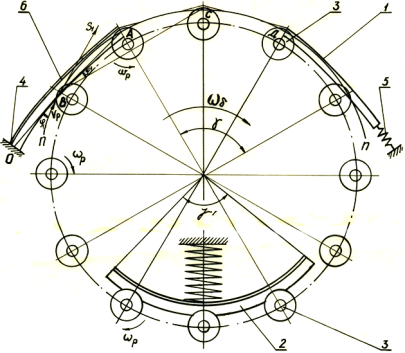
Рис. 1. Кинематическая схема привода шпинделей
Ввиду того, что угол между ремнем ![]() и направляющей силой
и направляющей силой ![]() определится удар, то из курса теоретической механики получим
определится удар, то из курса теоретической механики получим
![]() (1)
(1)
Износ ремня начинается с этого участка до конечной зоны реверса шпинделя. Из формулы (1) видно, скорость приводного ролика при реверсе шпинделя не является постоянной величиной ![]() , поэтому при уменьшении угла ребра
, поэтому при уменьшении угла ребра ![]() уменьшается функция
уменьшается функция ![]() и следовательно уменьшается
и следовательно уменьшается ![]() . Тогда при
. Тогда при ![]() , то сила удара приводного ролика по ремню также будет равна нулю.
, то сила удара приводного ролика по ремню также будет равна нулю.
Проводим плавные кривые, которые совпадают касательно с ударной силой ![]() . После удара ролика по ремню (рисунок 2) действует импульс
. После удара ролика по ремню (рисунок 2) действует импульс ![]() силы, которая направлена в точку полюса
силы, которая направлена в точку полюса ![]() . Линия
. Линия ![]() с касательной
с касательной ![]() составляет угол
составляет угол ![]() .
.
Построим точки пересечения других касательных ![]() с прямой
с прямой ![]() под углом
под углом ![]() и находим точки
и находим точки ![]() и т. д., соединяя эти точки получим кривую
и т. д., соединяя эти точки получим кривую ![]() . Составим уравнение касательной кривой
. Составим уравнение касательной кривой ![]() .
.
Для этого выводим уравнение окружности:
![]() (2)
(2)
и составим уравнение касательной к окружности (2)
![]()
или
![]() , (3)
, (3)
где ![]()
![]()
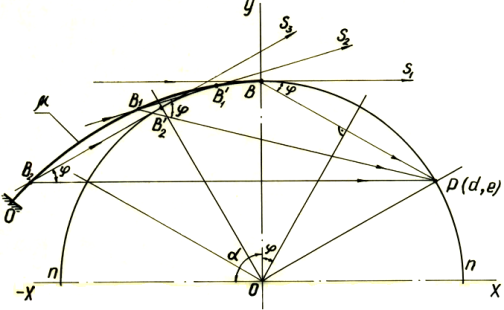
Рис. 2. Силовой расчет усилий в зоне привода прямого вращения шпинделей
Тогда подставляя данное значение в уравнение (3) имеем
![]() (4)
(4)
где ![]() — переменный угол, изменяющийся от 900 до
— переменный угол, изменяющийся от 900 до ![]() .
.
Тогда обозначим, что угол с абсциссой ![]() , через коэффициент
, через коэффициент ![]() , т. е.
, т. е.
![]()
Через точки полюса ![]() к касательному (4) по заданному условию, опускаем прямую под углом
к касательному (4) по заданному условию, опускаем прямую под углом ![]() .
.
Уравнение этой касательной кривой имеет следующий вид
![]() (5)
(5)
подставляя значения ![]() , получим:
, получим:
![]() (6)
(6)
Решаем совместно уравнение (4) и (6) для получения уравнения касательной кривой. Для этого из уравнения (4) находим ![]() и подставляя в уравнение (6) получим уравнение по абсциссе
и подставляя в уравнение (6) получим уравнение по абсциссе ![]() :
:
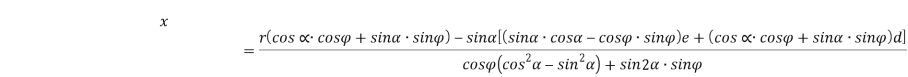 (7)
(7)
Также из уравнения (4) подставляя ![]() в (5) находим уравнение по ординате
в (5) находим уравнение по ординате ![]() :
:
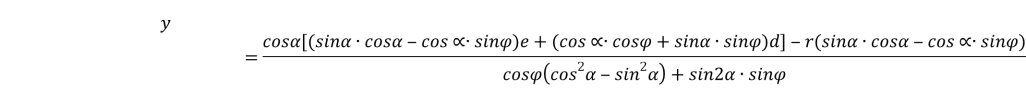 (8)
(8)
Окончательно получим уравнение в параметрическом виде:
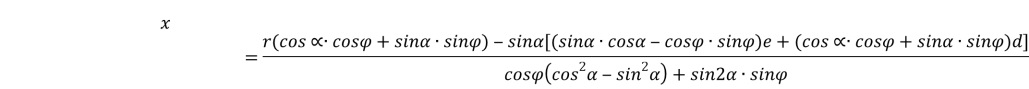
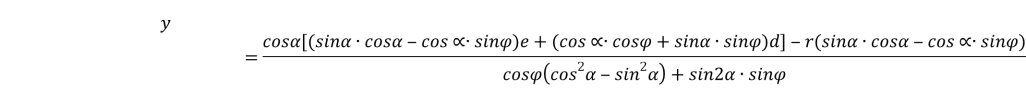 (9)
(9)
Полученное уравнение составляют параметрическое уравнение касательной кривой ![]() .
.
При движении сателлита ременной передачи планетарного механизма аппарата хлопкоуборочной машины.
На основании проведенного исследования можно сделать следующие выводы:
- Составлена математическая модель планетарного механизма с применением каркаса имеющую профиль дуги по касательной кривой и имеет по заданной форме эволюту.
- Конструкция кинематической схемы планетарного механизма позволяет за счет плавности захода роликов шпинделей в зону ременной передачи уменьшает износ рабочих поверхностей дорожки в два три раза.
- В связи с устранением ударной силы в момент реверса шпинделя при входе ролика в зоне прямого вращения ремня, то в значительной степени в целом увеличивается срок службы подшипников привода шпинделей.
Литература:
- Алимова Д. Б., Пулатова Х. А. Кинематическое исследование гибкого планетарного механизма для привода технологических машин. // Научный журнал «Молодой учёный» № 10(90), Часть II, май, 2015 г. Россия, г. Казань. — С. 132–134.

