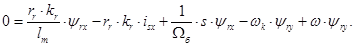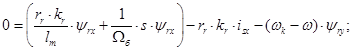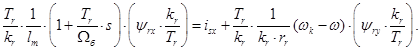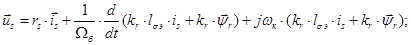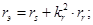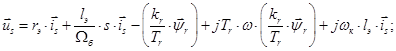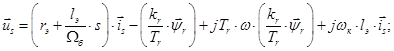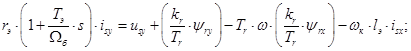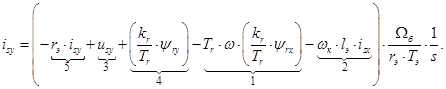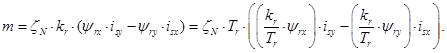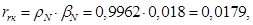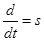Данная работа является развитием статьи [1], в которой переменные 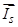 и
и 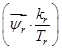 определялись на выходе апериодических звеньев. В этой статье эти переменные получены с интегрирующих звеньев, что существенно изменяет возможности математической модели асинхронного двигателя.
определялись на выходе апериодических звеньев. В этой статье эти переменные получены с интегрирующих звеньев, что существенно изменяет возможности математической модели асинхронного двигателя.
Так как работа адресована студентам, то выводы даны без сокращений. Предварительно, для лучшего понимания необходимо рассмотреть статьи [2], [3], [4]. В работе [2] подробно рассмотрены способы и технологии получения пространственных векторов 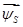 ,
, 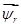 ,
, 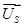 ,
, 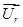 ,
, 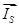 ,
, 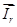 в системе абсолютных единиц. Были получены основные уравнения асинхронного двигателя в произвольной системе координат
в системе абсолютных единиц. Были получены основные уравнения асинхронного двигателя в произвольной системе координат 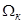 :
:
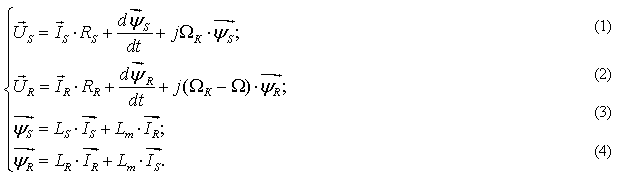
Переведем эти уравнения в систему относительных единиц.
В уравнениях (1) и (2) обе части разделим на 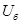 :
:
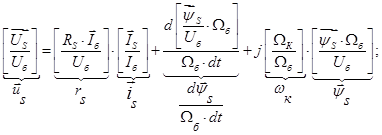
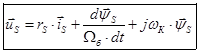 (5)
(5)
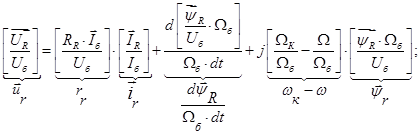
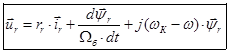 (6)
(6)
В уравнениях (3) и (4) обе части умножим на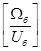 :
:
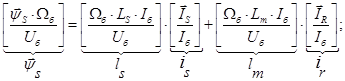
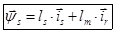 (7)
(7)
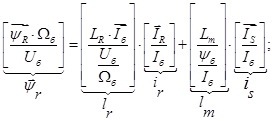
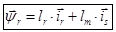 (8)
(8)
Итак, основные уравнения асинхронного двигателя с к. з. ротором (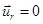 ) имеют следующий вид:
) имеют следующий вид:
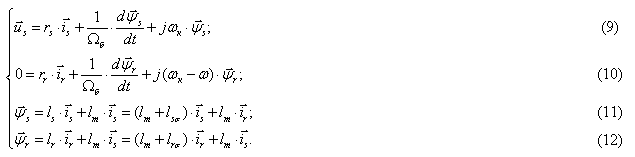
Электромагнитный момент определяется по формуле [5, c.131]:
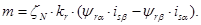 (13)
(13)
Уравнение движения:
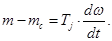 (14)
(14)
Так как электромагнитный момент определяется через переменные 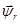 и
и 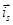 , то из уравнений исключим переменные
, то из уравнений исключим переменные 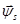 и
и 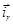 .
.
Из уравнения (12) выразим 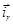 :
:
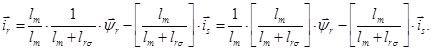
Обозначим 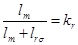 , тогда
, тогда
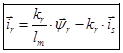 (15)
(15)
Из уравнения (11) исключим 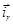 :
:
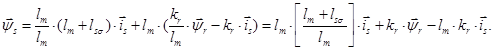
Обозначим 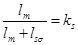 , тогда
, тогда
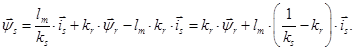
Преобразуем выражение в скобке:
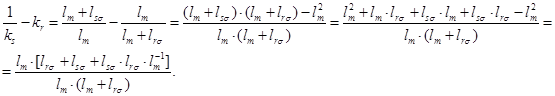
Обозначим 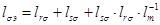 .
.
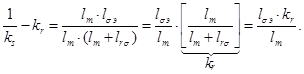
Тогда
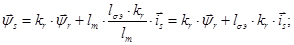
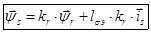 (16)
(16)
В уравнении (10) подставим 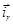 :
:
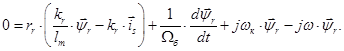 (17)
(17)
Отсюда выразим:
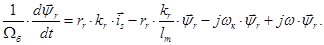 (18)
(18)
В уравнении (17) перейдем к изображениям 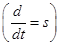 и разложим векторы
и разложим векторы 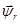 и
и 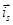 на проекции:
на проекции:
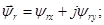
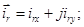
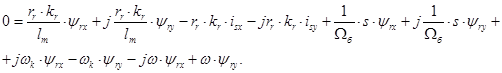 (*)
(*)
Проекция уравнения (*) на ось +1:
Проекция уравнения (*) на ось +j:
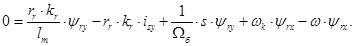 (20)
(20)
Из уравнения (20):
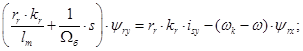
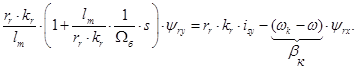
Разделим обе части полученного уравнения на (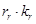 ):
):
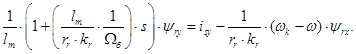
Преобразуем:
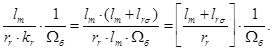
Обозначим 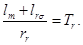
Тогда
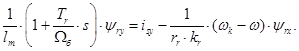
В соответствии с [6] перейдем к переменным 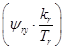 и
и 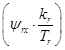 :
:
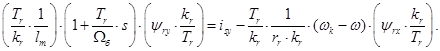
Выразим:
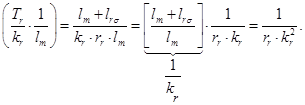
В результате получим уравнение, которое было рассмотрено нами в работе [1] при получении переменной 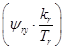 на выходе апериодического звена:
на выходе апериодического звена:
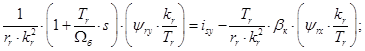
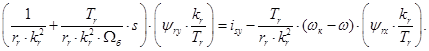
Для получения переменной 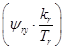 на выходе интегрирующего звена раскроем скобки в левой части:
на выходе интегрирующего звена раскроем скобки в левой части:
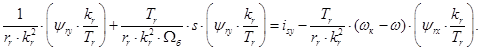
Перенесем первое слагаемое в левую часть:
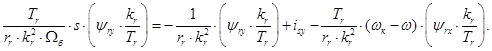
Наконец, переменная 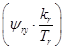 выразится через интегрирующее звено:
выразится через интегрирующее звено:
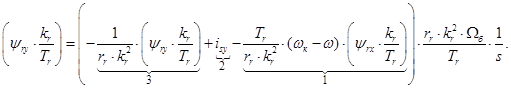 (21)
(21)
Этому уравнению (21) соответствует следующая структурная схема:
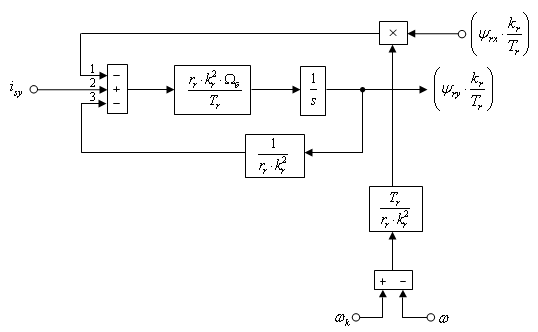
Рис. 1. Структурная схема для определения 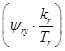
Аналогично для уравнения (19):
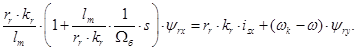
Выразим новые переменные 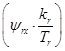 и
и 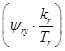 и разделим обе части уравнения на
и разделим обе части уравнения на 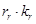 :
:
Обозначим 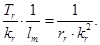
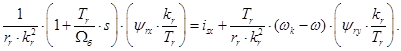
Для получения переменной 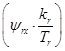 на выходе апериодического звена перенесем первое слагаемое в правую часть:
на выходе апериодического звена перенесем первое слагаемое в правую часть:
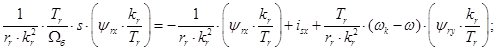
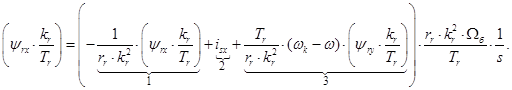 (22)
(22)
Полученному уравнению (22) соответствует следующая структурная схема:
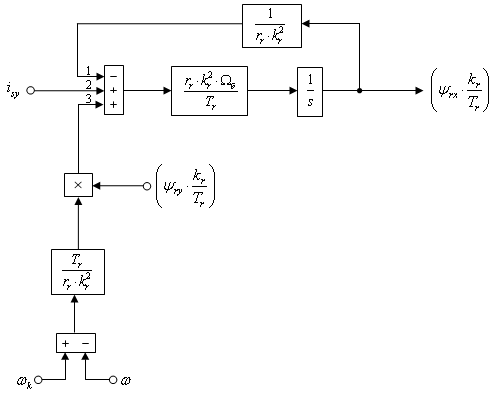
Рис. 2. Структурная схема для определения 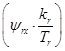
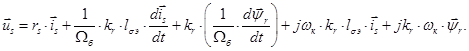
Подставим в это уравнение 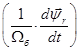 из уравнения (18):
из уравнения (18):
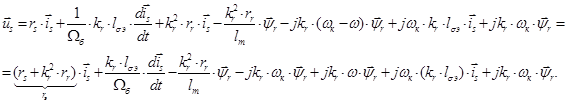
Введем обозначения:
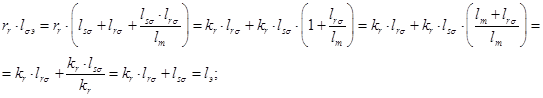
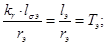
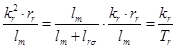 ,
,
где 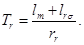
Переведем уравнение 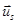 в изображения, для этого выразим
в изображения, для этого выразим 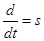 :
:
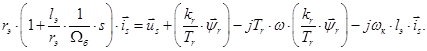
Выразим векторы 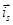 ,
, 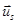 и
и 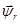 через проекции:
через проекции:
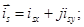
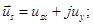
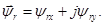
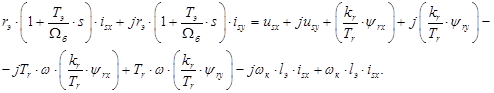 (**)
(**)
Проекция уравнения (**) на действительную ось +1:
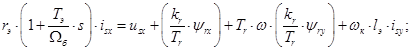
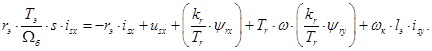 (23)
(23)
Проекция уравнения (**) на мнимую ось +j:
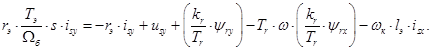 (24)
(24)
Из уравнения (23) выразим 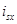 :
:
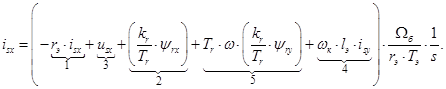
Структурная схема для реализации тока 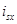 в MatLab-Simulink дана на рис. 3.
в MatLab-Simulink дана на рис. 3.
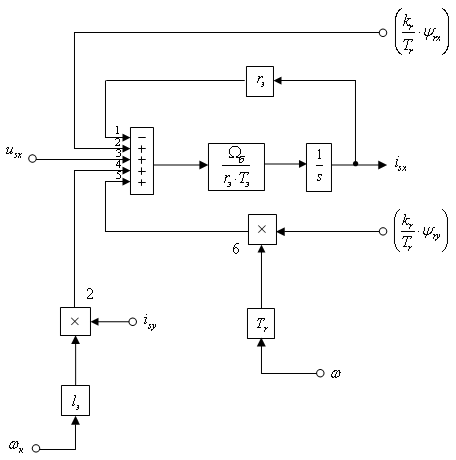
Рис. 3. Структурная схема проекции статорного тока 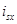 на ось +1
на ось +1
Аналогично из уравнения (24) выразим 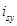 :
:
Структурная схема, соответствующая этому уравнению представлена на рис. 4.
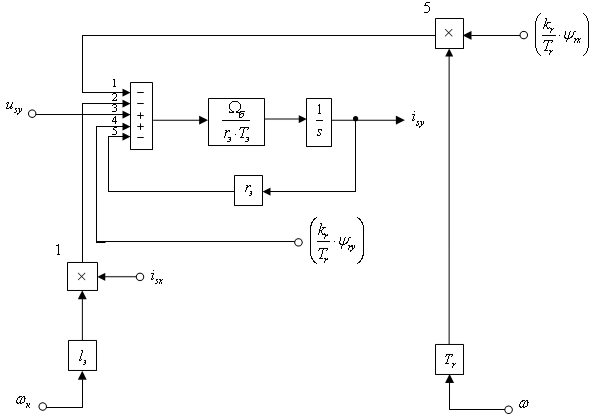
Рис. 4. Структурная схема проекции статорного тока 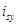 на ось +j
на ось +j
Структурная схема для реализации уравнения (13) дана на рис. 5:
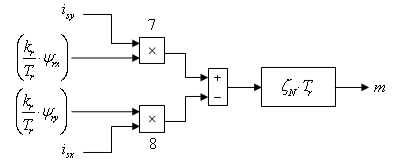
Рис. 5. Математическая модель электромагнитного момента m
Наконец для уравнения (14):
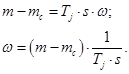
Структурная схема дана на рис. 6.

Рис. 6. Математическая модель уравнения движения
В работе [5] в главе 6 «Примеры» дан образец расчета параметров асинхронного двигателя. В наших дальнейших работах направленных на подготовку студентов к исследовательской работе, глава 6 окажет неоценимую помощь. Можно было бы по аналогии рассмотреть паспортные данные любого другого двигателя, но для проверки правильности выводов уравнений сделанных исследовательской группой самостоятельно, необходимо постоянно выходить на многие полученные результаты в работе [6]. Поэтому, этот пример расчета окажется очень полезным.
Номинальные данные:
Номинальный режим работы S1;
Номинальная мощность 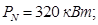
Номинальное фазное напряжение 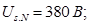
Номинальный фазный ток 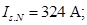
Номинальная частота .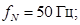
Номинальная синхронная скорость 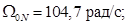
Номинальная скорость ротора 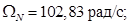
Номинальный КПД 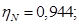
Номинальный коэффициент мощности 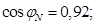
Число пар полюсов 
Параметры Т-образной схемы замещения при номинальной частоте:
Активное сопротивление обмотки статора 
Индуктивное сопротивление рассеяния обмотки статора 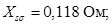
Активное сопротивление обмотки ротора, приведенное к статору 
Индуктивное сопротивление рассеяния обмотки ротора, приведенное статору 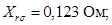
Главное индуктивное сопротивление 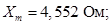
Суммарный момент инерции двигателя и механизма 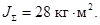
Базисные величины системы относительных единиц:
Напряжение 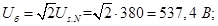
Ток 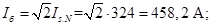
Частота 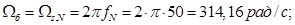
Скорость ротора 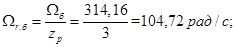
Сопротивление 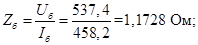
Потокосцепление 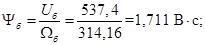
Индуктивность 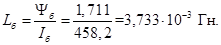
Используя номинальные данные двигателя, определяем:
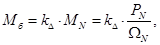
где 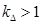 — коэффициент, учитывающий различие значений электромагнитного момента и момента на валу двигателя в номинальном режиме (
— коэффициент, учитывающий различие значений электромагнитного момента и момента на валу двигателя в номинальном режиме (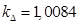 ).
).
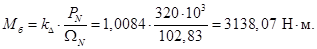
В качестве базисной мощности выбираем значение электромагнитной мощности двигателя в номинальном режиме, определяемое по следующей формуле:
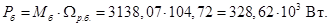
Относительные значения параметров схемы замещения двигателя:
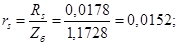
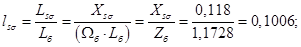
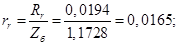
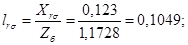
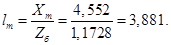
Механическая постоянная времени:
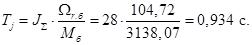
Номинальное значение скольжения:
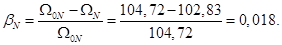
Относительное значение номинальной скорости ротора:
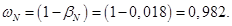
Нормирующий энергетический коэффициент:
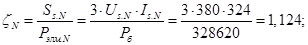
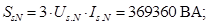
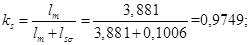
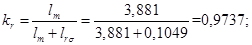
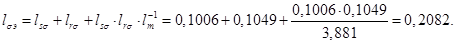
При расчете режимов работы, для того чтобы 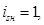
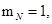
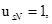
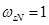 и
и 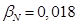 необходимо откорректировать
необходимо откорректировать 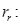
где 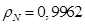 — корректирующий коэффициент [5, с. 296].
— корректирующий коэффициент [5, с. 296].
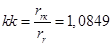 — коэффициент, показывающий отношение
— коэффициент, показывающий отношение 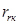 к
к 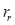 .
.
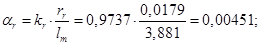
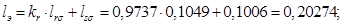
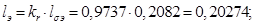
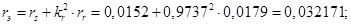
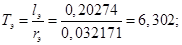
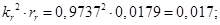
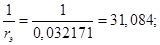
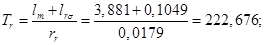
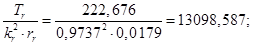
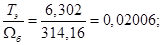
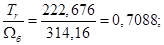
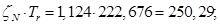
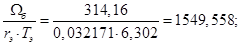
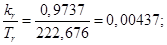
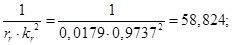
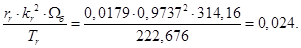
На рис. 7 представлена система, состоящая из математической модели АД, преобразователя координат и блока ориентации.
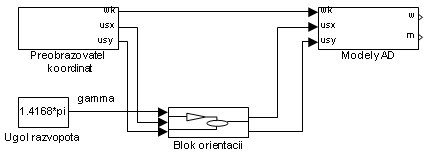
Рис. 7. Общий вид системы
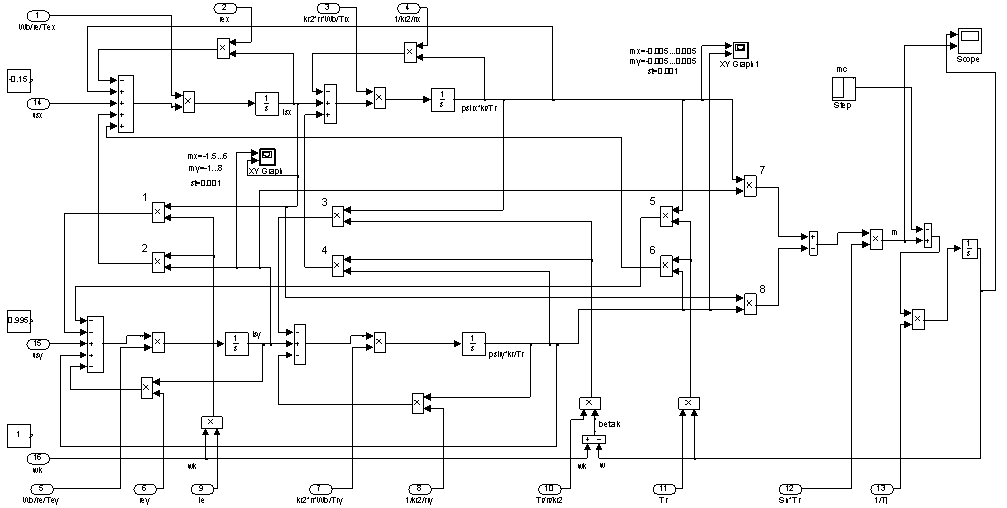
Главным элементом этой системы является математическая модель асинхронного двигателя. Основным отличием от модели двигателя, приведенного в работе [1] является то, что переменные 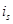 и
и 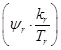 формируются на выходе интегрирующих звеньев. Это позволяет вынести расчет коэффициентов модели в отдельную подсистему (Raschet koefficientov). В результате этого выноса остается оболочка из сумматоров, блоков перемножения и интеграторов (Obolochka dvigatela). Общая структура двигателя дана на рис. 8.
формируются на выходе интегрирующих звеньев. Это позволяет вынести расчет коэффициентов модели в отдельную подсистему (Raschet koefficientov). В результате этого выноса остается оболочка из сумматоров, блоков перемножения и интеграторов (Obolochka dvigatela). Общая структура двигателя дана на рис. 8.
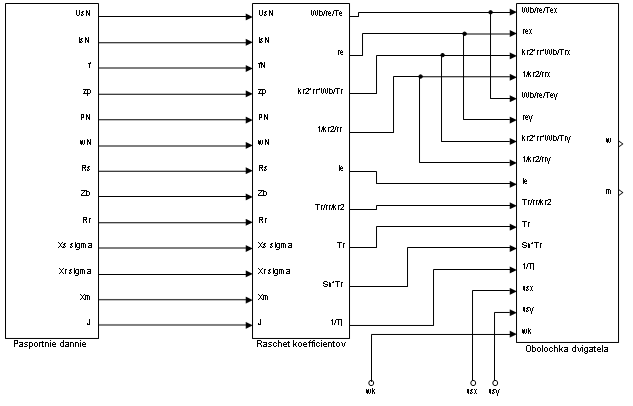
Рис. 8. Модель асинхронного двигателя (оболочка двигателя, расчет параметров и ввод паспортных данных)
Оболочка двигателя дана на рис. 9. Ввод паспортных данных двигателя показан на рис. 10. Особенностью этого структурного элемента подсистемы состоит в том, что он предусматривает различные варианты справочных данных. В некоторых справочниках даны параметры двигателя в относительных единицах и для того, чтобы максимально приблизиться к структуре подачи материала главы 6 [5], в которой вначале параметры двигателя даны в абсолютных единицах в блоке (Pasportnie dannie) установлены ключи manual switch (рис. 10). В этом случае ключи необходимо перевести в нижнее положение.
Расчет коэффициентов осуществляется в подсистеме Raschet koefficientov, приведенной на рис. 11.
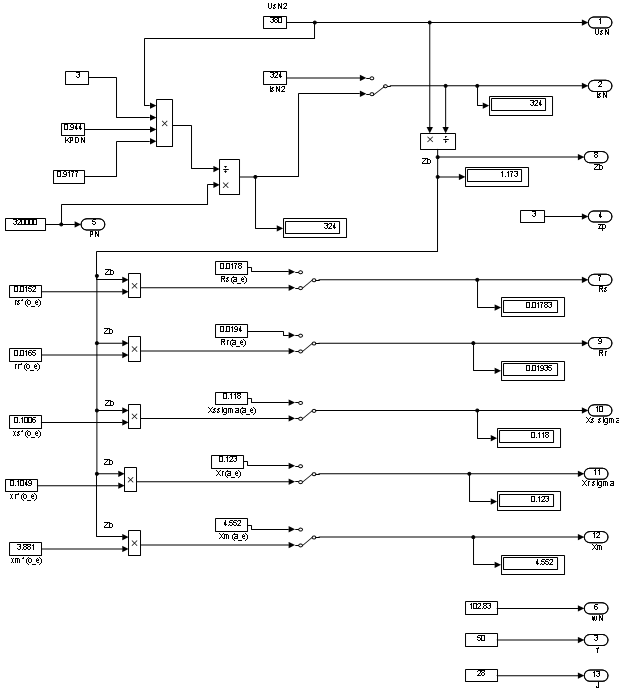
Рис. 10. Паспортные данные
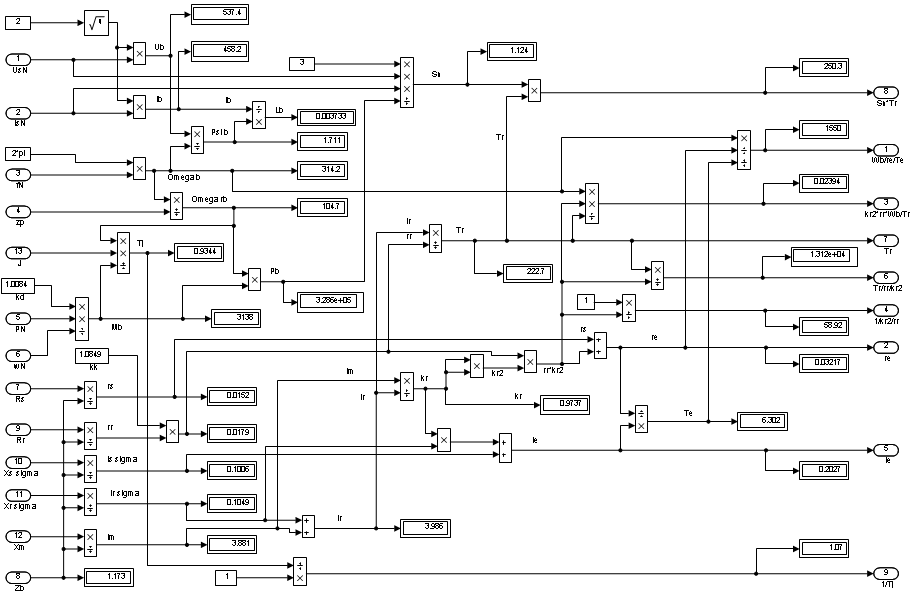
Рис. 11. Расчет коэффициентов
Следующим важным элементом системы (рис. 7) является преобразователь координат, главная функция которого состоит в том, чтобы перевести математическую модель асинхронного двигателя в систему координат, синхронно вращающуюся с частотой сети ωк=ωs. В этом случае на вход математической модели необходимо подавать постоянные значения usx и usy. Преобразователь координат состоит из трех подсистем (рис. 12):
- формирователь мгновенных значений трехфазного напряжения usa, usb и usc (Subsystemusa, usb, usc);
- подсистема, обеспечивающая переход от трехфазной неподвижной системы 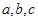 к двухфазной неподвижной системе. На выходе этого блока вычисляются проекции вращающегося вектора
к двухфазной неподвижной системе. На выходе этого блока вычисляются проекции вращающегося вектора 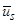
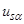 и
и 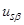 , которые представляют собой мгновенные значения напряжения синусоидальной формы со сдвигом на 90°;
, которые представляют собой мгновенные значения напряжения синусоидальной формы со сдвигом на 90°;
- подсистема, производящая переход от неподвижной двухфазной системы к вращающейся системе, в которой usx и usy имеют постоянные значения.
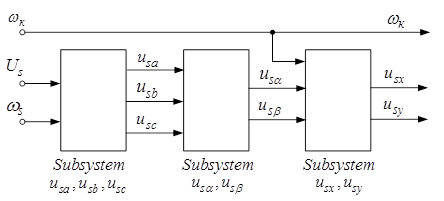
Рис. 12. Преобразователь координат
Рассмотрим каждый из этих элементов отдельно:
1. Subsystemusa, usb, usc.
Как известно, мгновенные значения трехфазного напряжения определяются через следующие формулы:
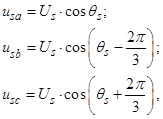
где 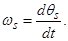
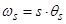 или
или 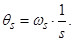
Эти зависимости реализованы в Simulink-Matlab по следующей схеме (рис. 13):
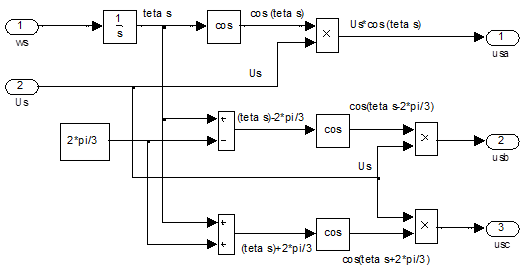
Рис. 13. Subsystem usa, usb, usc
2. Subsystem 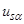 ,
, 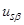 .
.
Переход от трех мгновенных значений usa, usb, usc к пространственному вектору 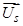 , вращающемуся со скоростью
, вращающемуся со скоростью 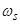 в неподвижной системе координат
в неподвижной системе координат 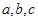 или, наоборот, проекции вращающегося вектора
или, наоборот, проекции вращающегося вектора 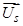 на неподвижные оси
на неподвижные оси 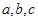 дают мгновенные значения usa, usb, usc, которые были рассмотрены в работе [2].
дают мгновенные значения usa, usb, usc, которые были рассмотрены в работе [2].
Можно этот же вращающийся вектор 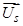 получить в двухфазной машине. Для этого необходимо питать эти обмотки от двух синусоидальных напряжений
получить в двухфазной машине. Для этого необходимо питать эти обмотки от двух синусоидальных напряжений 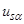 и
и 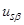 со взаимным сдвигом на 90°, или, наоборот, взяв проекции этого вращающегося вектора в неподвижной системе координат, получим мгновенные значения
со взаимным сдвигом на 90°, или, наоборот, взяв проекции этого вращающегося вектора в неподвижной системе координат, получим мгновенные значения 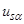 и
и 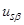 (рис. 14).
(рис. 14).
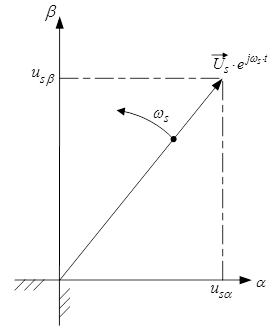
Рис. 14. Проекции вращающегося вектора 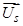 на неподвижные оси α и β
на неподвижные оси α и β
Связь между мгновенными значениями usa, usb, usc и 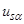 ,
, 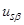 следующая [6, с. 551–553]:
следующая [6, с. 551–553]:
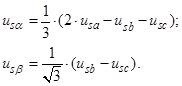
Реализация этих уравнений в Simulink-Matlab представлена на рис. 15.
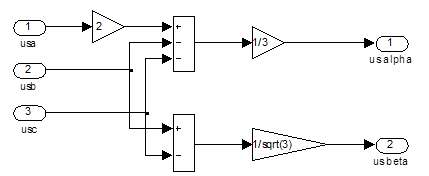
Рис. 15. Subsystem 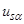 ,
, 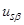
Переход от проекций 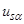 и
и 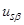 вращающегося вектора
вращающегося вектора 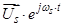 в неподвижной системе координат (α, β) к проекциям этого вектора во вращающейся системе координат
в неподвижной системе координат (α, β) к проекциям этого вектора во вращающейся системе координат 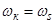 показан на рис. 15.
показан на рис. 15.
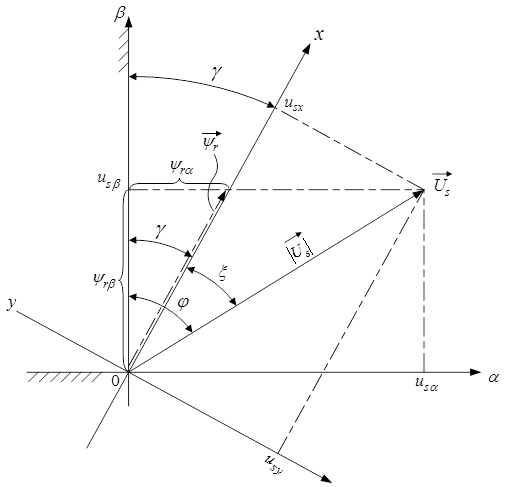
Рис. 15. Пересчет проекций вектора 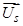 при переходе из одной системы координат в другую
при переходе из одной системы координат в другую
Для пояснения этого перехода рассмотрим формулы пересчета:
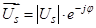 .
.
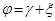 — угол поворота вектора
— угол поворота вектора 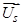 по отношению к
по отношению к 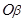 в системе координат
в системе координат 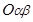 .
.
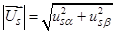 — модуль вектора
— модуль вектора 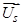 .
.
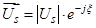 — этот же вектор в системе координат
— этот же вектор в системе координат 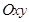 .
.
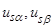 — проекции вектора
— проекции вектора 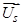 на оси
на оси 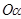 и
и 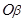 в системе координат
в системе координат 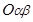 .
.
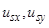 — проекции вектора
— проекции вектора 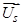 на оси
на оси 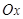 и
и 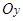 в системе координат
в системе координат 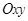 .
.
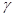 — угол поворота между осями.
— угол поворота между осями.
Пусть новая система координат 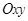 сориентирована по вектору потокосцепления обмотки ротора
сориентирована по вектору потокосцепления обмотки ротора 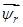 , тогда координатные функции поворота
, тогда координатные функции поворота 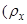 и
и 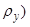 определятся по следующим зависимостям:
определятся по следующим зависимостям:
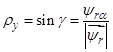 и
и 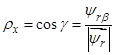 ,
,
где 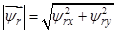 .
.
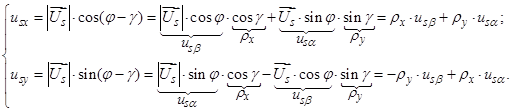
Для системы, вращающейся со скоростью 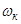 полученные выражения можно записать в следующем виде:
полученные выражения можно записать в следующем виде:
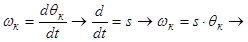
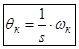 .
.
Обозначим 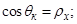
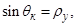 тогда [6, с. 552]:
тогда [6, с. 552]:
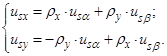
Реализация этих формул в Matlab-Simulink показана на рис. 16.
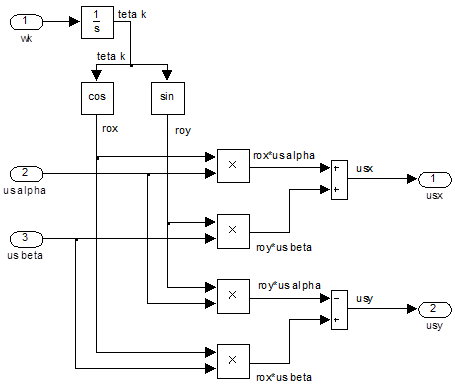
Рис. 16. Subsystemusx, usy
Общий вид преобразователя координат дан на рис. 17.
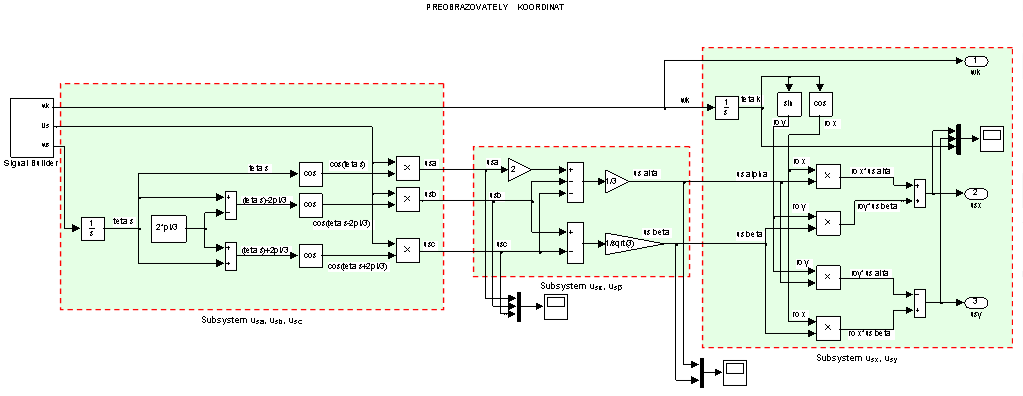
Рис. 17. Общий вид преобразователя координат
Последний элемент системы (рис. 7) блок ориентации в своей основе повторяет Subsystem 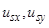 . Для учебных целей этот элемент системы необходимо выделить в отдельный блок. Изменяя γ (gamma), можно совместить систему координат с одним из векторов, например
. Для учебных целей этот элемент системы необходимо выделить в отдельный блок. Изменяя γ (gamma), можно совместить систему координат с одним из векторов, например 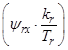 , т. к. постоянная времени для потокосцеплений
, т. к. постоянная времени для потокосцеплений 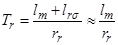 во много раз больше постоянных времени, связанных с индуктивностями рассеяния
во много раз больше постоянных времени, связанных с индуктивностями рассеяния 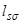 или
или 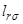 .
.
Блок ориентации, реализованный в Simulink-Matlab, представлен на рис. 18.
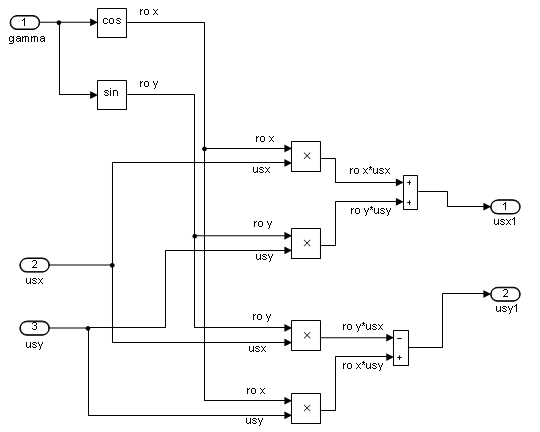
Рис. 18. Блок ориентации
Результаты моделирования системы представлены на рис. 19…23.
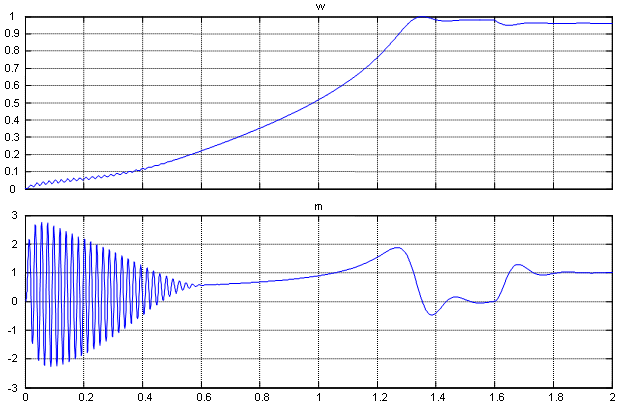
Рис. 19. Графики скорости и момента
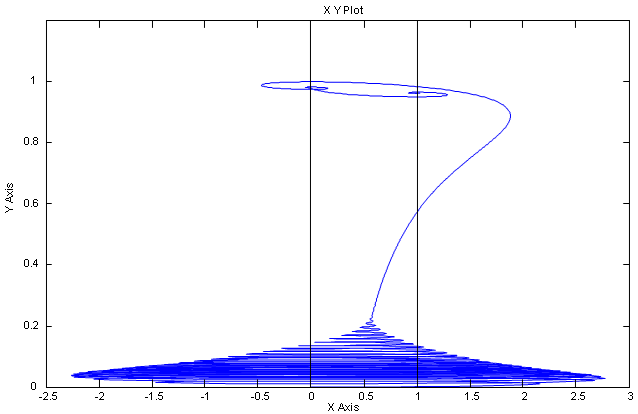
Рис. 20. Динамическая механическая характеристика при пуске и набросе нагрузки
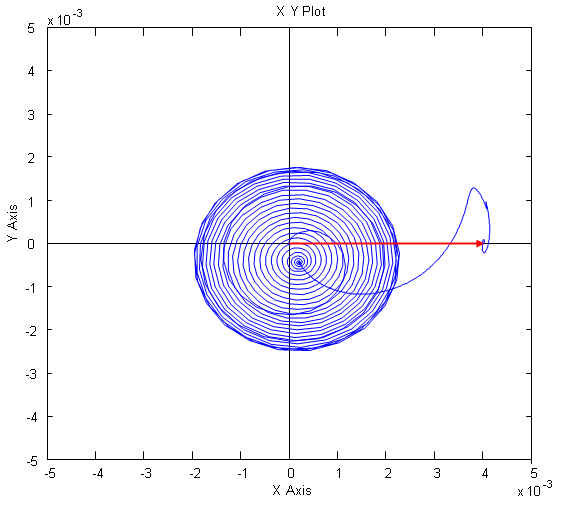
Рис. 21. Ориентация системы координат по потокосцеплению ротора
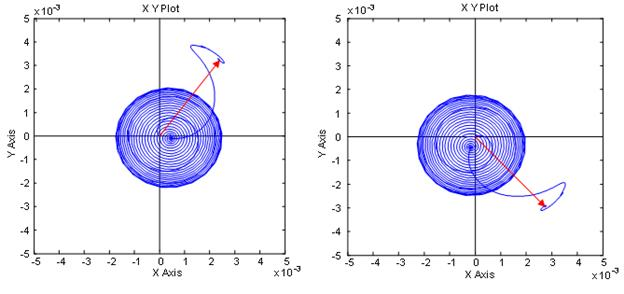
Рис. 22. Произвольная ориентация системы координат
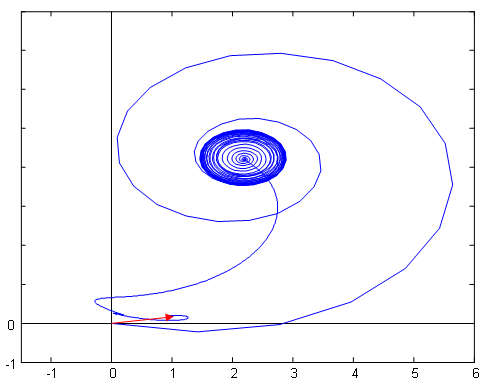
Рис. 23. Годограф изменения статорного тока 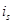 при пуске
при пуске
Литература:
1. Емельянов А. А., Козлов А. М., Бесклеткин В. В., Авдеев А. С., Чернов М. В., Киряков Г. А., Габзалилов Э. Ф., Фуртиков К. А., Реутов А. Я., Королёв О. А. Математическая модель асинхронного двигателя с переменными 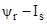 в произвольной системе координат // Молодой ученый. — 2015. — № 14. — С.
в произвольной системе координат // Молодой ученый. — 2015. — № 14. — С.
2. Емельянов А. А., Козлов А. М., Бесклеткин В. В., Авдеев А. С., Чернов М. В., Киряков Г. А., Габзалилов Э. Ф., Фуртиков К. А., Реутов А. Я., Королёв О. А. Пространственные векторы в асинхронном двигателе в относительной системе единиц // Молодой ученый. — 2015. — № 11. — С. 133–156.
3. Емельянов А. А., Козлов А. М., Бесклеткин В. В., Авдеев А. С., Чернов М. В., Киряков Г. А., Габзалилов Э. Ф., Фуртиков К. А., Реутов А. Я., Королёв О. А. Математическая модель асинхронного двигателя с короткозамкнутым ротором в неподвижной системе координат с переменными 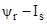 // Молодой ученый. — 2015. — № 13. — С. 20–31.
// Молодой ученый. — 2015. — № 13. — С. 20–31.
4. Медведев А. В., Емельянов А. А., Клишин А. В. Математическая модель асинхронного двигателя в неподвижной системе координат с переменными ir — ψr // Молодой ученый. — 2010. — № 4. — С. 8–24.
5. Шрейнер Р. Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р. Т. Шрейнер, А. В. Костылев, В. К. Кривовяз, С. И. Шилин. Под ред. проф. д.т.н. Р. Т. Шрейнера. — Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. — 361 с.
6. Шрейнер Р. Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. — Екатеринбург УРО РАН, 2000. — 654 с.