«Всякий, кто изучает простые числа, бывает очарован и одновременно ощущает собственное бессилие. Определение простых чисел так просто и очевидно; найти очередное простое число так легко; разложение на простые сомножители — такое естественное действие. Почему же простые числа столь упорно сопротивляются нашим попыткам постичь порядок и закономерности их расположения? Может быть, в них вообще нет порядка, или же мы так слепы, что не видим его?.. " — так писал о простых числах Ч. Уэзерелл [7, с. 88]. И этот порядок математики пытаются увидеть уже тысячелетия. Не один пытливый талантливый ум ученого пытался решить задачу отыскания простых чисел: Эратосфен, Пифагор, Ферма, Чебышев и многие другие.
Но, изучая вклад ученых-математиков в развитие учения о простых числах, замечаешь, что иногда в редких источниках встречается фамилия уральского математика Ивана Михеевича Первушина. А вот найти его труды или более подробную информацию о научной деятельности проблематично, сведения чаще всего отрывочны и разрознены. Так, какой вклад в развитие теории простых чисел внес уральский математик И. М. Первушин?
Иван Михеевич Первушин (рис. 1) — известный математик, священник и краевед.

Рис. 1. И. М. Первушин (1827–1900)
И. М. Первушин родился 21 января 1827 года в г. Лысьве Пермской губернии в семье церковного пономаря. В 1838 г. Иван Первушин становится учеником пермского духовного училища. Здесь, как вспоминал Первушин, «познакомился я с числами и арифметикой, заняла мысль «о простых числах», не давала мне покою и периодически отнимала у меня много времени и труда письменного» [3, с. 2].
После окончания училища в 1842 г., его приняли в духовную семинарию, окончив курс обучения в семинарии в 1848 г. первым учеником, единственный из выпуска был отправлен на обучение в Казанскую духовную академию, которую он окончил кандидатом богословия. На выпускном экзамене присутствовал академик П. Л. Чебышев, который высоко оценил математические способности студента И. Первушина и подарил ему книгу со своими заметками.
По окончании духовного учебного заведения Первушин служил сначала в Перми, затем в селе Замараево Шадринского уезда, где прожил 25 лет. Здесь он в своем доме открыл первую в селе школу, издавал рукописный журнал «Шадринский вестник» с очень смелыми для того времени мыслями. Своей просветительской деятельностью Первушин навлек на себя гонения властей. Вскоре школа «за неимением средств к содержанию» была закрыта, а чуть позже прекращен и выпуск журнала. После этого Иван Первушин углубляется в математику и краеведение.
Как и многих его предшественников и современников, Первушина занимал вопрос о простых и составных числах. Книга П. Л. Чебышева «Теория сравнений» оказала большое влияние на Первушина, досконально изучив её, он вплотную принялся за исследование теории чисел.
Предположение Ферма, что числа 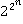 +1 простые при всяком n, долгое время оставалось предметом поисков Первушина. В ноябре 1877 г. Петербургская Академия наук получила письмо, в котором Первушин сообщил, что он обнаружил новое составное число, а именно, 22¹² + 1, которое делится на 114689.
+1 простые при всяком n, долгое время оставалось предметом поисков Первушина. В ноябре 1877 г. Петербургская Академия наук получила письмо, в котором Первушин сообщил, что он обнаружил новое составное число, а именно, 22¹² + 1, которое делится на 114689.
Эти результаты обратили на себя внимание специалистов. Академик В. Я. Буняковский на заседании физико-математического отделения Академии наук доложил, что «священник Первушин в записке от 18 ноября 1877 года сообщил Академии о новом открытом им случае делимости чисел вида 22ⁿ +1, а именно 22¹² + 1». Заметка об открытии была опубликована в «Записках Академии».
В новой своей записке в январе 1878 г. Первушин сообщал о другом случае делимости вышеприведённой формулы, он нашёл, что число 22²³ +1 также составное и делится на 16777216. Академик Е. И. Золотарёв проверил и подтвердил этот результат. О математике с Урала заговорили в академических кругах.
Начиная с 1877 г., Первушин почти в течение двадцати лет состоял в переписке с Петербургской Академией наук, посылая туда свои математические труды. Известно, что он представил свыше двадцати записок, большинство которых посвящено вопросам делимости, в том числе и записку о знаменитом простом числе Первушина.
Как известно из истории математической науки, во время работы Первушина над теорией простых чисел в науке было известно самое большое простое число 2³¹-1 = 2147483647, открытое математиком Эйлером. И это число как высокий предел открытий в этом направлении держалось канонически уже около века. Но уральский священник Иван Михеевич Первушин доказал, что число, большее открытого Эйлером, а именно 261–1 = 2305843009213693851 — тоже простое. Это открытие вызвало сенсацию в математических кругах, и имя уральского математика прочно вошло в историю математических открытий. Хотя в дальнейшем ученые математики открыли простые числа — большие «первушинского», но открытое уральцем число до сих пор известно как «число Первушина».
В 1893 г. работа И. М. Первушина «О наилучшей проверке арифметических действий над огромными числами при посредстве делителей: 103–2=998, 104–2=9998» была представлена на Математическом конгрессе в Чикаго, которая была единственной из России. Затем он представил работу «Об определении количества простых чисел в известных пределах», которую предложила Неаполитанская академия физико-математического королевского общества.
Много сил, времени и упорного труда отдал И. М. Первушин составлению таблиц простых чисел, которые являются его крупнейшим достижением. Он посвятил этому труду более сорока лет (1854–1897) своей жизни и составил простых чисел таблицы до 10 000 000. Это были первые обширные таблицы простых чисел в России. Петербургская Академия наук нашла невозможным опубликовать таблицы Первушина из-за их большого объема (на 750 листах, заполненных мелким бисерным почерком), и рукопись была передана на хранение в архив Академии наук. К сожалению, этот огромный труд Первушина остался забытым некоторыми позднейшими математиками, даже занимавшимися теорией чисел.
В октябре 1893 г. научная общественность всего мира отмечала столетний юбилей русского математика Н. И. Лобачевского. При Казанском физико-математическом обществе был организован учредительный комитет по созданию капитала имени великого математика для премирования выдающихся произведений в области геометрии. И. М. Первушин был избран почетным членом этого комитета.
За свои достижения в математике был избран членом-корреспондентом Петербургской, Неаполитанской и Парижской академий наук. Первушин — член Московского, Казанского ученых математических обществ, Уральского общества любителей естествознания.
Умер И. М. Первушин 30 июня 1900 г. с. Мехонском Шадринского уезда.
Сведения об уральском математике содержатся в Большой советской энциклопедии, Уральской исторической энциклопедии, энциклопедическом словаре Брокгауза и Ефрона. Его исследования переплетаются с исследованиями Ферма, Эйлера и др. математиков, ценной и важной является его таблица простых чисел, он далеко расширил её пределы, «Число Первушина» вошло во все математические энциклопедии (таблица 1).
Таблица 1
Вклад И. М. Первушина в науку
|
№ п/п |
Открытие |
В мире |
И. М. Первушин |
|
1. |
Формула простого числа |
Утверждение П. Ферма (1601–1665):
Л.Эйлер опроверг утверждение при n=5: число |
Опроверг при n=12 (1877 г.): 22¹² + 1 делится на 114689. Опроверг при n=23 (1878 г.): 22²³ +1 делится на 16777216. |
|
2. |
Большие простые числа |
Леонард Эйлер (1707–1783)
|
«Число Первушина»: 261–1= 2305843009213693851 |
|
3. |
Таблицы простых чисел |
1) Катальди (1603) — до 750 2) Шутен (1657) — до 10 000 |
до 10 000 000 (1854–1897) |
Иван Михеевич Первушин — талантливый русский математик, замечательный вычислитель, жизнь которого не прошла бесследно для науки.
Литература:
1. Ганеев Х. Ж. Учителю математики об элементах краеведения. Кн. для учителя / Урал. гос. пед. ун-т Екатеринбург, 1996.
2. За страницами учебника математики: Арифметика. Алгебра. Геометрия: Кн. для учащихся 10–11 кл. общеобразоват. учреждений / Н.Я Виленкин, Л. П. Шибасов, З. Ф. Шибасова. — М.: Просвещение: АО «Учеб. Лит»., 1996. — 320 с.
3. Красноперова Н. В. Родом из Лысьвы: Иван Михеевич Первушин и его семья / [Электронный ресурс] / — Режим доступа: http://encyclopaedia.lysva.ru/9/9–15.pdf.
4. Первушин Иван Михеевич. Материал из Википедии / [Электронный ресурс] / — Режим доступа: http://ru.wikipedia.org/wiki
5. Перунов В. К. Культурное наследие Зауралья: справочное пособие. — Шадринск, 2012. — 80 с.
6. Раик А. Е. Уральский математик Иван Михеевич Первушин// «Историко-математические исследования», 1953, вып. VI..- стр. 535–572.
7. Уэзерелл Ч. Этюды для программистов. — М.: Мир, 1982. — 288 с.
8. Федосеева Л. В. Зауральский математик И. М. Первушин/ [Электронный ресурс]/ — Режим доступа: http://www.zavuch.info/methodlib/52/99848.
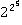 +1 — составное
+1 — составное