Способность создавать и оперировать пространственными образами характеризует уровень общего интеллектуального развития человека. В психологических исследованиях экспериментально подтверждено, что между склонностью человека к соответствующим профессиям и уровнем развития пространственных представлений имеет место статистически достоверная связь. Широкое применение невозможных фигур в архитектуре, живописи, психологии, геометрии и во многих других областях практической жизни дают возможность больше узнать о различных профессиях и определиться с выбором будущей профессии.
Ключевые слова: трибар, бесконечная лестница, космическая вилка, невозможные ящики, треугольник и лестница Пенроуза, куб Эшера, треугольник Рейтерсвэрда.
Цель исследования: изучение свойств невозможных фигур с помощью с помощью 3-D моделей.
Задачи исследования:
- Изучить виды и составить классификацию невозможных фигур.
- Рассмотреть способы построения невозможных фигур.
- Создать невозможные фигуры с помощью компьютерной программы и 3D моделирования.
Понятие невозможных фигур
Объективного понятия «невозможные фигуры» не существует. Из одного источника невозможная фигура — вид оптических иллюзий, фигура, кажущаяся проекцией обычного трёхмерного объекта, при внимательном рассмотрении которой становятся видны противоречивые соединения элементов фигуры. А из другого источника невозможные фигуры — это геометрически противоречивые изображения объектов, не существующих в реальном трёхмерном пространстве. Невозможность возникает из противоречия между подсознательно воспринимаемой геометрией изображённого пространства и формально-математической геометрией.
Анализируя разные определения, приходим к выводу:
невозможная фигура — это плоский рисунок, который создает впечатление трехмерного объекта таким образом, что объект, предложенный нашим пространственным восприятием, не может существовать, так что попытка создать его ведет к (геометрическим) противоречиям, ясно видимыми наблюдателем.
Когда мы смотрим на изображение, которое создает впечатление пространственного объекта, наша система пространственного восприятия пытается найти пространственную форму, определить ориентацию и структуру, начиная с анализа отдельных фрагментов и намеков на глубину. Далее, эти отдельные части комбинируются и координируются в некотором порядке для создания общей гипотезы о пространственной структуре объекта целиком. Обычно, несмотря на то, что плоское изображение может иметь бесконечное множество пространственных интерпретаций, наш механизм интерпретации выбирает только одну — наиболее естественную для нас. Именно эта интерпретация изображения далее проверяется на возможность или невозможность, а не сам рисунок. Невозможная интерпретация получается противоречивой по своей структуре — различные частичные интерпретации не подходят к общему непротиворечивому целому.
Фигуры являются невозможными, если их естественные интерпретации оказываются невозможными. Однако, это не подразумевает, что не существует какой-либо другой интерпретации этой же фигуры, которая может существовать. Таким образом, нахождение метода точного описания пространственных интерпретаций фигур является одним из основных путей для дальнейшей работы с невозможными фигурами и механизмами их интерпретации. Если суметь описать различные интерпретации, то можно будет сравнивать их, соотносить фигуру и ее различные интерпретации (понять механизмы создания интерпретаций), проверять их соответствие или определять типы несоответствия и т. п.
Виды невозможных фигур
Невозможные фигуры разделяются на два больших класса: одни имеют реальные трехмерные модели, а для других такие создать невозможно.
В ходе работы над темой изучены 4 вида невозможных фигур: трибар, бесконечная лестница, невозможные ящики и космическая вилка. Все они уникальны по-своему.
Трибар (треугольник Пенроуза)

Это геометрически невозможная фигура, элементы которой не могут быть соединены. Все-таки невозможный треугольник стал возможным. Шведский живописец Оскар Рейтесвэрд в 1934 г. впервые представил миру невозможный треугольник из кубиков. В честь этого события в Швеции издана почтовая марка. Трибар можно сделать из бумаги. Любители оригами нашли способ создать и подержать в руках вещь, которая казалась ранее запредельной фантазией ученого. Однако нас обманывают собственные глаза, когда мы смотрим на проекцию трехмерного объекта из трех перпендикулярных линий. Наблюдателю кажется, что он видит треугольник, хотя на самом деле это не так.
Бесконечная лестница.

Конструкция, которая не имеет ни конца, ни края, была придумана биологом Лейонелем Пенроузом и его сыном-математиком Роджером Пенроузом. Впервые модель была опубликована в 1958 г., после чего получила большую популярность, стала классической невозможной фигурой, а ее основная концепция нашла применение в живописи, архитектуре, психологии. Модель ступеней Пенроуза обрела самую большую популярность по сравнению с остальными нереальными фигурами в сфере компьютерных игр, головоломках, оптических иллюзиях. «Вверх по ступеням, ведущим вниз» — так можно охарактеризовать лестницу Пенроуза. Идея этой конструкции заключается в том, что при движении по часовой стрелке ступени ведут все время вверх, а в обратном — вниз. При этом «вечная лестница» состоит всего из четырех пролетов. А значит, всего через четыре лестничных марша путник оказывается там же, откуда начал движение.
Невозможные ящики.

Еще один невозможный объект появился в 1966 году в Чикаго в результате оригинальных экспериментов фотографа доктора Чарльза Ф. Кокрана. Многие любители невозможных фигур проводили эксперименты с «Сумасшедшим ящиком». Первоначально автор назвал ее «свободным ящиком» и заявил, что она была «сконструирована для пересылки невозможных объектов в большом количестве». «Сумасшедший ящик» — это вывернутый наизнанку каркас куба. Непосредственным предшественником «Сумасшедшего ящика» была «Невозможная коробка» (автор Эшер), а ее предшественником в свою очередь стал куб Неккера. Он не является невозможным объектом, однако представляет собой фигуру, в которой параметр глубины может восприниматься неоднозначно. Когда мы вглядываемся в куб Неккера, то замечаем, что грань с точкой находится то на переднем, то на заднем плане, она перепрыгивает из одного положения в другое.
Космическая вилка.

Среди всех невозможных фигур особое место занимает невозможный трезубец («космическая вилка»). Если закрыть рукой правую часть трезубца, то мы увидим вполне реальную картину — три круглых зуба. Если закрыть нижнюю часть трезубца, то мы тоже увидим реальную картину - два прямоугольных зубца. Но, если рассматривать всю фигуру целиком, то получается, что три круглых зубца постепенно превращаются в два прямоугольных.
Таким образом, можно увидеть, что передний и задний планы данного рисунка конфликтуют. То есть, то что было изначально на переднем плане уходит назад, а задний план (средний зуб) вылезает вперед. Кроме смены переднего и заднего планов в данном рисунке присутствует еще один эффект — плоские грани правой части трезубца становятся круглыми в левой. Эффект невозможности достигается за счет того, что наш мозг анализирует контур фигуры и пытается подсчитать количество зубцов. Мозг сравнивает количество зубцов фигуры в левой и правой части рисунка, из-за чего возникает ощущение невозможности фигуры. Если количество зубцов у фигуры было значительно больше (например, 7 или 8), то этот парадокс был бы менее ярко выражен.
Изготовление моделей невозможных фигур по чертежам
Трехмерная модель — это физически представимый объект, при рассмотрении которого в пространстве становятся видимыми все щели и изгибы, которые уничтожают иллюзию невозможности, и данная модель теряет свое «волшебство». При проецировании данной модели на двухмерную плоскость получается невозможная фигура. Эта невозможная фигура (в отличие от трехмерной модели), создает впечатление невозможного объекта, который может существовать только в воображении человека, но не в пространстве.
Трибар
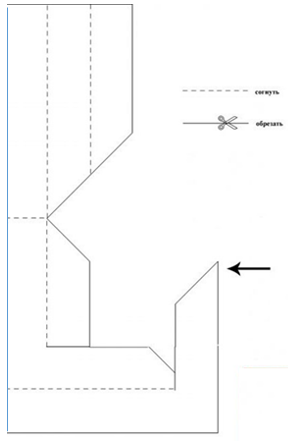
Бумажная модель:

Невозможный брусок
Чертеж:
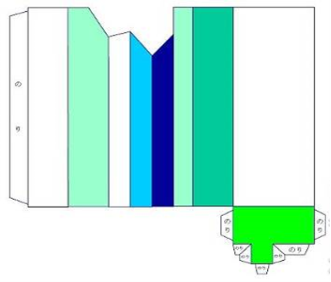
Бумажная модель:


Построение невозможных фигур в программе Impossible Constructor
Программа Impossible Constructor предназначена для конструирования изображений невозможных фигур из кубиков. Основными недостатками этой программы были сложность выбора нужного кубика (отыскать один нужный кубик из 32-х доступных в программе достаточно тяжело), а также то, что не были предусмотрены все варианты кубиков. Предлагаемая программа предоставляет к выбору полный набор кубиков (64 кубика), а также дает более удобный способ нахождения требуемого кубика при помощи конструктора кубиков.
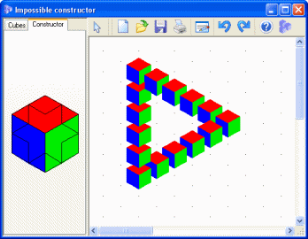
Моделирование невозможных фигур.
Печать 3D моделей невозможных фигур на принтере
В ходе работы модели четырех невозможных фигур распечатаны на 3D принтере.
Треугольник Пенроуза
Процесс создания трибара:


Вот что у меня получилось в итоге:

Куб Эшера
Процесс создания куба: В конечном итоге получена модель:


Лестница Пенроуза (всего через четыре лестничных марша путник оказывается там же, откуда начал движение):

Треугольник Рейтерсвэрда (первый невозможный треугольник, состоявший из девяти кубиков):


Процесс подготовки к печати дал возможность на практике научиться строить стереометрические фигуры на плоскости, выполнять проекции элементов фигур на заданную плоскость и продумывать алгоритмы построения фигур. Созданные модели помогли наглядно увидеть и проанализировать свойства невозможных фигур, сравнить их с известными стереометрическими фигурами.
«Если не можешь изменить ситуацию, взгляни на нее под другим углом».
Эта цитата непосредственно относится к данной работе. Действительно, невозможные фигуры существуют, если взглянуть на них под определенным углом. Мир невозможных фигур чрезвычайно интересен и многообразен. Они существуют с древних времен по наше время. Их можно встретить практически везде: в искусстве, архитектуре, в массовой культуре, в живописи, в иконописи, в филателистике. Невозможные фигуры представляют большой интерес для психологов, когнитивистов и эволюционных биологов, помогая больше узнать о нашем зрении и пространственном мышлении. Сегодня компьютерные технологии, виртуальная реальность и проекции расширяют возможности, так что на противоречивые объекты можно взглянуть с новым интересом. Существует множество профессий, которые так или иначе связаны с невозможными фигурами. Все они востребованы в современном мире, а потому изучение невозможных фигур является актуальным и нужным.
Литература:
- Реутерсвард О. Невозможные фигуры. — М.: Стройиздат,1990, 206 с.
- Левитин Карл Геометрическая рапсодия. — М.: Знание, 1984, -176 с.
- Пенроуз Л., Пенроуз Р. Невозможные объекты, Квант, № 5,1971, с.26
- Ткачева М. В. Вращающиеся кубики. — М.: Дрофа, 2002. — 168 с.
- http://www.im-possible.info/russian/articles/reut_imp/
- http://www.impworld.narod.ru/.
- Левитин Карл Геометрическая рапсодия. — М.: Знание, 1984, -176 с.
- http://www.geocities.jp/ikemath/3Drireki.htm
- http://im-possible.info/russian/programs/
- https://www.liveinternet.ru/users/irzeis/post181085615
- https://newtonew.com/science/impossible-objects
- http://www.psy.msu.ru/illusion/impossible.html
- http://referatwork.ru/category/iskusstvo/view/73068_nevozmozhnye_figury
- http://geometry-and-art.ru/unn.html

