В данной статье рассматривается зависимость архимедовой силы, действующей на тело в жидкости (воде), от температуры тела. При проведении различных лабораторных работ, связанных с архимедовой силой, действующей на тело в жидкости (воде), необходимо учитывать температуру тела.
Ключевые слова: архимедова сила, температура, плотность жидкости, коэффициент объёмного расширения, объём тела, вода
В статье [1, с. 60] рассматривалась зависимость архимедовой силы от температуры жидкости (воды) и был сделан вывод: с увеличением температуры воды архимедова сила уменьшается. При этом не учитывалось влияние температуры жидкости (воды) на изменение объёма тела, находящегося в ней. Тепловое состояние тела характеризуется его температурой. Общеизвестный факт, что все металлы при нагревании расширяются, а при охлаждении сжимаются. Степень увеличения или уменьшения первоначального размера металлического тела при изменении температуры на один градус характеризуется коэффициентом линейного расширения. При наблюдении за изменением объёма тела (металла) используют коэффициент объёмного расширения, который определяется как утроенный коэффициент линейного расширения [2, с. 112].
Выясним, как изменяются линейные размеры твёрдого тела (алюминиевого цилиндра) вследствие изменения температуры. Для этого измерим длину и диметр алюминиевого цилиндра, потом нагреем его, опустив в горячую воду. Затем, спустя некоторое время, измерив вновь размеры цилиндра, можно заметить, что цилиндр незначительно увеличился. Таким образом, делаем вывод: тепловое расширение алюминиевого цилиндра зависит от температуры. Тепловое расширение и охлаждение приходится принимать во внимание при расчёте архимедовой силы. При тепловом расширении алюминиевого цилиндра с увеличением линейных размеров увеличивается и его объём.
«Обозначив объём алюминиевого цилиндра при 0°С через V0, объём при температуре t° через Vt, а коэффициент объёмного расширения через β, найдём:
![]() , (1)
, (1)
где ∆ t = t — t0 — изменение температуры тела» [3,с.187].
Сначала рассчитаем по формуле (1) объём алюминиевого цилиндра при t=4°С, используя следующие известные физические величины: объём цилиндра при t0=20°С, V0=17,34∙10–6м3 и β=3α=3∙22,9∙10–6°С-1=68,7∙10–6°С-1, взятые из различных источников Интернета. Подставив исходные данные в выражение (1), получим:
V=17,34∙10–6м3∙(1+68,7∙10–6°С-1(4°С–20°С))=17,34∙0,9989∙10–6м3=17,32∙10–6м3. (2)
А теперь рассчитаем по формуле (1) объём алюминиевого цилиндра при t0=25°С, используя следующие физические величины: объём цилиндра при t0=20°С,V0=17,34∙10–6м3 и β=3α=3∙23∙10–6°С-1=69∙10–6°С-1, взятые из различных источников Интернета. Подставив исходные данные в выражение (1), получим:
V’=17,34∙10–6м3∙(1+69∙10–6°С-1(25°С–20°С))=17,34∙1,000345∙10–6м3=17,346∙10–6м3. (3)
Сравним полученные значения объёма алюминиевого цилиндра, воспользовавшись отношением:
![]() . (4)
. (4)
Вывод: с увеличением температуры объём тела, погруженного в жидкость (воду), увеличивается.
При охлаждении и нагревании алюминиевого цилиндра изменяется его объём. Учитывая, что архимедова сила и объём тела, погруженного в воду, пропорциональны друг другу, получаем:
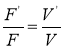 , (5)
, (5)
где F’ — архимедова сила при t=25°С, F — архимедова сила при t=4°С.
Тогда, используя выражения (4) и (5), получим: 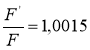 .
.
Вывод: с увеличением объёма тела, погруженного в воду, архимедова сила увеличивается.
Рассчитаем архимедову силу по формуле: ![]() , (6)
, (6)
с учётом изменения плотности воды и объёма алюминиевого цилиндра, используя следующие физические величины: плотность воды (при 25°С) 996,95![]() , ускорение свободного падения g = 9,81
, ускорение свободного падения g = 9,81 ![]() и объём тела (при 25°С) 17,346∙10–6 м3.
и объём тела (при 25°С) 17,346∙10–6 м3.
Используя выражение (6) и численные значения физических величин, будем иметь: ![]() .
.
А теперь, используя выражение (6), рассчитаем архимедову силу без учёта изменения плотности воды и объёма тела. Для этого воспользуемся следующими численными значениями физических величин: плотности воды 1000![]() , ускорение свободного падения g = 9,81
, ускорение свободного падения g = 9,81 ![]() и объём тела 17,34∙10–6 м3:
и объём тела 17,34∙10–6 м3:
![]()
Сравним полученные значения архимедовой силы, воспользовавшись отношением: 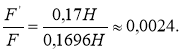
Вывод: архимедова сила без учёта изменения плотности воды и объёма тела, больше архимедовой силы с учётом изменений, зависящих от температуры.
Литература:
- Абдурашидов А. М. «Ещё раз об архимедовой силе». Международный научный журнал «Юный учёный». № 5(08)/2016. с.60.
- Енохович А. С. Справочник по физике и технике. // Просвещение. Москва. 1989. с.112.
- Яворский Б. М., Селезнёв Ю. А. Справочное руководство по физике. Москва. 1975. с.187.

