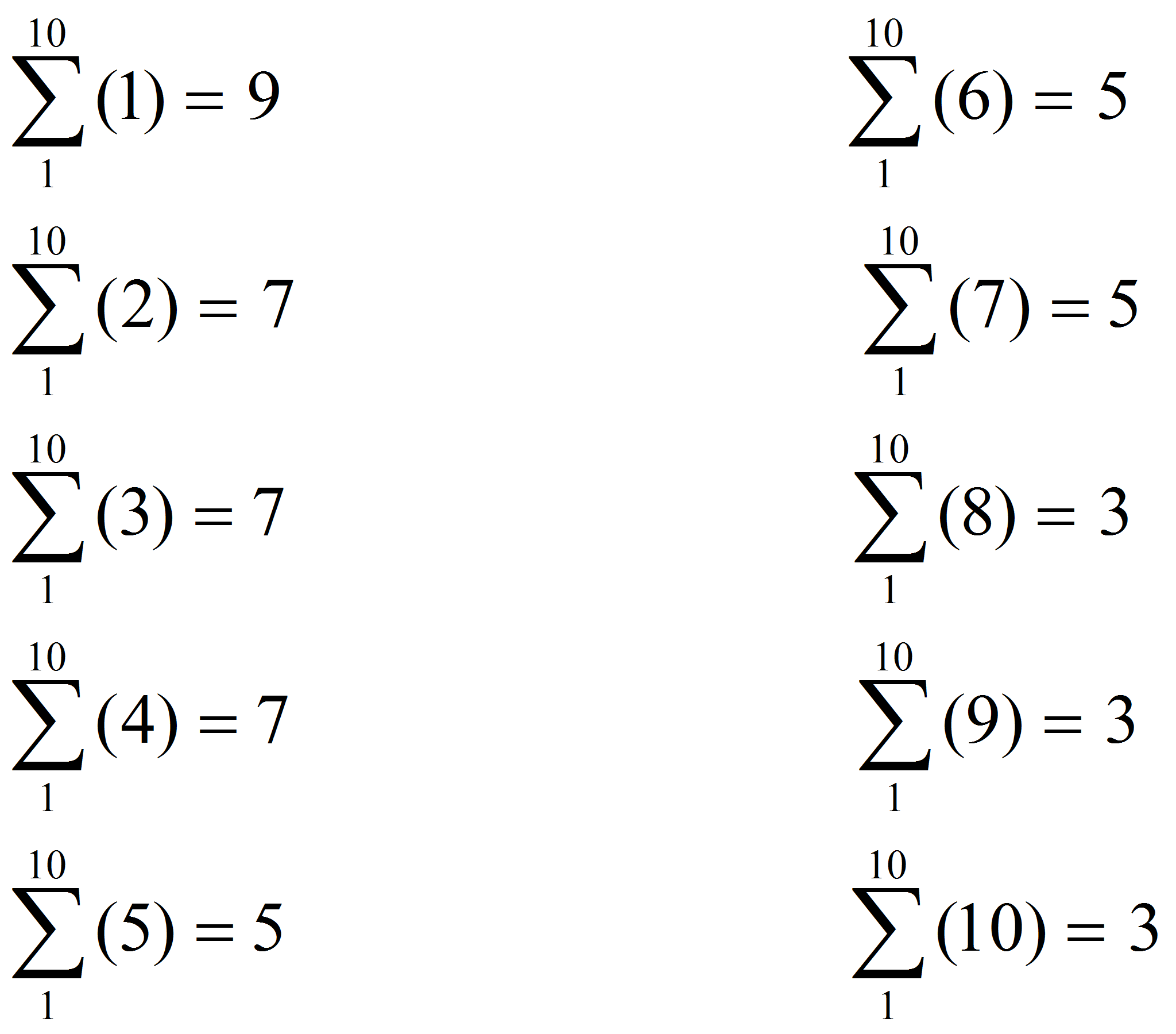Разработка методики оценки ранга элемента в системе возникновения электрической машины
Авторы: Идиятуллин Ринат Гайсович, Смердова Татьяна Евгеньевна, Вдовин Александр Михайлович, Попов Александр Владимирович
Рубрика: 4. Электротехника
Опубликовано в
международная научная конференция «Технические науки в России и за рубежом» (Москва, май 2011)
Статья просмотрена: 706 раз
Библиографическое описание:
Идиятуллин, Р. Г. Разработка методики оценки ранга элемента в системе возникновения электрической машины / Р. Г. Идиятуллин, Т. Е. Смердова, А. М. Вдовин, А. В. Попов. — Текст : непосредственный // Технические науки в России и за рубежом : материалы I Междунар. науч. конф. (г. Москва, май 2011 г.). — Москва : Ваш полиграфический партнер, 2011. — С. 51-54. — URL: https://moluch.ru/conf/tech/archive/3/708/ (дата обращения: 27.10.2024).
Увеличивающаяся сложность электротехнических устройств; возрастающая ответственность функций, которые выполняют технические устройства; повышение требований к качеству изделий и условиям их работы; возросшая роль автоматизации, которая сокращает возможность непрерывного наблюдения за состоянием устройства, - основные факторы, определившие главное направления в развитии науки о надёжности. Технические средства и условия их работы становятся всё более сложными. Количество элементов в отдельных видах устройств исчисляется сотнями тысяч. Если не принимать специальных мер по обеспечению надёжности, то любое современное сложное устройство практически будет неработоспособным. Техническим средствам отводят всё более ответственные функции на производстве и в сфере управления. Отказ технического устройства зачастую может привести к катастрофическим последствиям. Надёжность в эпоху научно-технической революции стала важнейшей проблемой.
Решая вопрос относительно распределения усилий по обеспечению надежности отдельных элементов в целях достижения заданной надежности системы, иногда необходимо знать, какой элемент наиболее значимый, какой - менее значимый. Иначе говоря, необходимо знать, какое влияние оказывает на общую надежность системы выход из строя того или иного ее элемента.
На начальных этапах проектирования достаточно определить значимость элемента некоторыми структурными параметрами. И, наоборот, анализировать и оценивать качество схемы этими структурными параметрами значимости. Впоследствии необходимо, конечно, уточнять показатели значимости, дополнив их параметрами, характеризующими функционирование системы и определяющими эффективность ее функционирования.
На начальном этапе для такой оценки обычно отсутствуют исходные данные. Количественная оценка значимости впервые явно была сформулирована при анализе структуры отношений доминирования (превосходства, преобладания) в группах индивидуумов. В качестве индивидуумов будем рассматривать основные элементы, из которых состоит генератор.
Шаг 1. Анализ электрической схемы генератора.
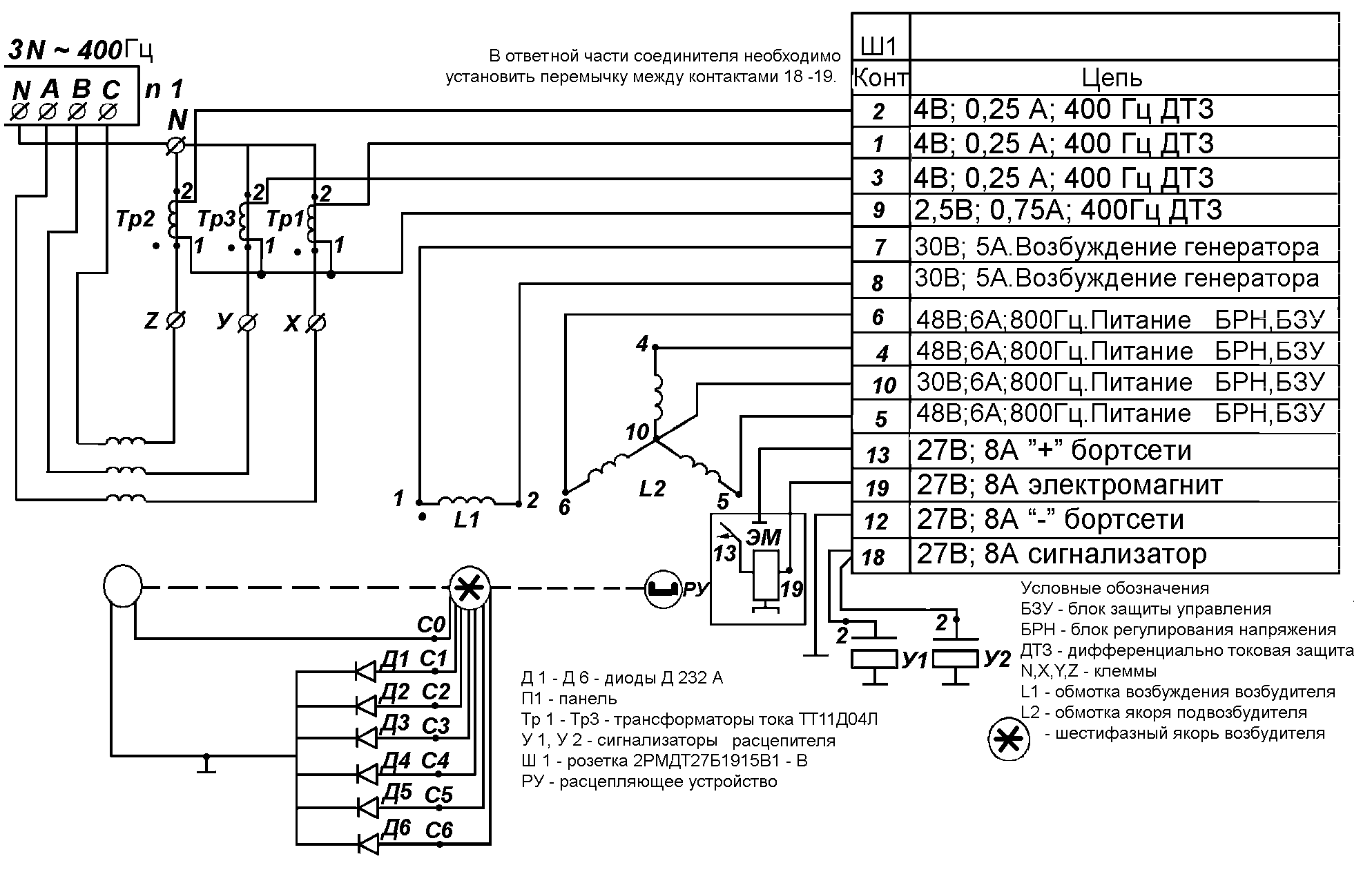
Рис.1 Схема принципиальная электрическая генератора ГТ40ПЧ8Б (ГТ40ПЧ8В).
Однако для построения графа нам важны элементы генератора, обозначенные в его электрической схеме. Рассмотрим фрагмент электрической схемы. Выделяем следующие элементы:
1. клемма N
2. клемма A
3. клемма B
4. клемма C
5. клемма X
6. клемма Y
7. клемма Z
8. трансформатор ТР1
9. трансформатор ТР2
10. трансформатор ТР3
Шаг 2. Составление структурной схемы.
Для составления структурной схемы будем использовать теорию графов.
Теория графов - раздел конечной математики, особенностью которого является геометрический подход к изучению объектов. Основное понятие теории - граф. Граф задаётся множеством вершин (точек) и множеством рёбер (связей), соединяющих некоторые (а может быть, и все) пары вершин. При этом пары вершин могут соединяться несколькими ребрами. В нашем случае пример графов - это элементы электрической схемы и провода, соединяющие их. Число вершин графа равняется числу рассматриваемых элементов в электрической цепи.
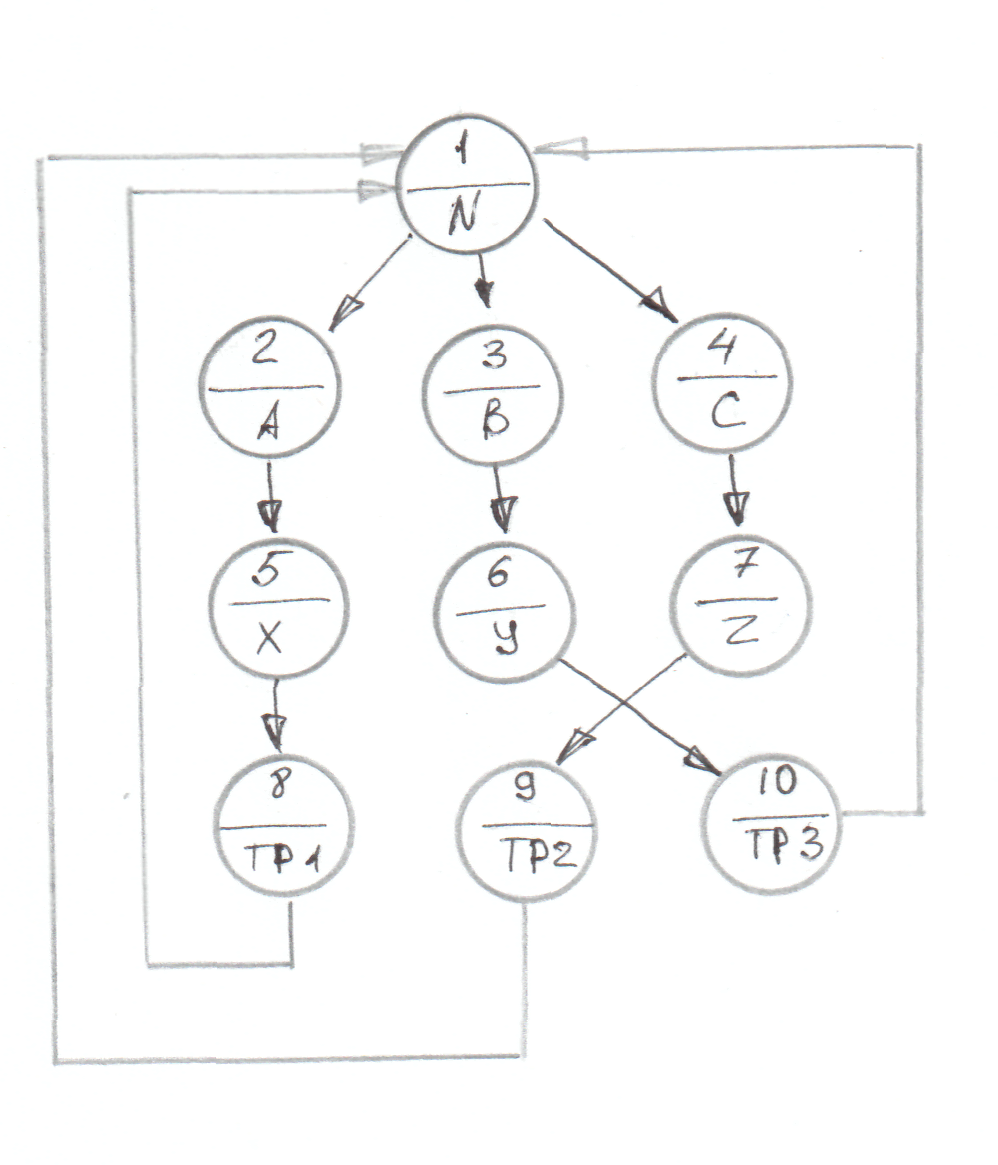
Рисунок 2. Граф фрагмента электрической схемы генератора ГТ40ПЧ8Б (ГТ40ПЧ8В)
Шаг 3. Составление матрицы непосредственных путей.
Матрица непосредственных путей есть не что иное, как аналитический образ графа, его аналитическая форма записи, его математическая модель. Процесс построения матрицы непосредственных путей А сводится к следующему.
3.1 Определяется порядок матрицы. Он равен числу вершин в исходном графе.
3.2 Вершины исходного графа нумеруются в произвольном порядке.
3.3. Этими же номерами обозначаются строки и столбцы матрицы.
3.4 Элемент, принадлежащий i-й строке и j-му столбцу, будет равен 1, если от вершины i к вершине j имеется непосредственный путь, и равен нулю в противном случае.
Для графа фрагмента электрической схемы генератора (см. рисунок 2) находим матрицу непосредственных путей (см. таблица1).
Таблица 1
Матрица непосредственных путей -А.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
2 |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
3 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
4 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
5 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
6 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
7 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
8 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
9 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
10 |
Шаг 4. Определение ранга каждого элемента матрицы.
При анализе структуры отношений доминирования значимость того или
иного индивидуума определяется некоторым числом, называемым рангом.
Этот параметр позволяет распределить элементы схемы в порядке их
значимости. Ранг i-го элемента R(i)
определится как сумма элементов i-ой строки
матрицы:
![]() .
Полученную матрицу R показываем в виде
таблицы 2.
.
Полученную матрицу R показываем в виде
таблицы 2.
Таблица 2
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
3 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
|
1 |
2 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
2 |
|
1 |
1 |
2 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
3 |
|
1 |
1 |
1 |
2 |
0 |
0 |
1 |
0 |
1 |
0 |
4 |
|
1 |
1 |
0 |
0 |
2 |
0 |
0 |
1 |
0 |
0 |
5 |
|
1 |
0 |
1 |
0 |
0 |
2 |
0 |
0 |
0 |
1 |
6 |
|
1 |
0 |
0 |
1 |
0 |
0 |
2 |
0 |
1 |
0 |
7 |
|
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
8 |
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
9 |
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
10 |
Складываем между собой элементы каждой строки матрицы. Получаем:
Как видим, клемма N имеет самое большое значение ранга.
Как видно из примера, определение значимости
элемента рангом по формуле
![]() осуществляется достаточно просто. Однако оно недостаточно полное., а
главное, неоднозначное. Остается неясным, что делать в случае
одинаковых рангов и какова значимость элемента, имеющего нулевой
ранг.
осуществляется достаточно просто. Однако оно недостаточно полное., а
главное, неоднозначное. Остается неясным, что делать в случае
одинаковых рангов и какова значимость элемента, имеющего нулевой
ранг.
Литература:
Идиятуллин Р.Г. Методика расчета остаточного ресурса изоляции высоковольтных синхронных машин. Сборник докладов « Перспективные технологии электроэнергетики». IX Международный симпозиум. М. 29-31 мая 2007 г.
Нечипоренко В.И. Структурный анализ и методы построения надежных систем. «Советское радио» 1968г. 256 стр.
Болотин Д.Н. Обобщенный граф и его использование при расчете радиотехнических схем. Радиотехника. 1965. т.20 №1.