Анализ существующих алгоритмов перевода функции алгебры логики в вероятностную функцию при расчете эксплуатационной надежности технических средств системы управления движением судов
Автор: Тюфанова Анастасия Александровна
Рубрика: 9. Транспорт
Опубликовано в
V международная научная конференция «Современные тенденции технических наук» (Казань, май 2017)
Дата публикации: 24.04.2017
Статья просмотрена: 209 раз
Библиографическое описание:
Тюфанова, А. А. Анализ существующих алгоритмов перевода функции алгебры логики в вероятностную функцию при расчете эксплуатационной надежности технических средств системы управления движением судов / А. А. Тюфанова. — Текст : непосредственный // Современные тенденции технических наук : материалы V Междунар. науч. конф. (г. Казань, май 2017 г.). — Казань : Бук, 2017. — С. 49-54. — URL: https://moluch.ru/conf/tech/archive/230/12283/ (дата обращения: 27.10.2024).
Рассмотрены существующие алгоритмы перевода функции алгебры логики в вероятностную функцию при расчете эксплуатационной надежности технических средств системы управления движением судов.
Ключевые слова: функция алгебры логики, алгоритм, технические средства, система управления движением судов
Обеспечением безопасности мореплавания на акватории порта и на подходах к нему занимается система управления движением судов (СУДС), работающая согласно международным и национальным правовым и нормативным актам, над повышением уровня безопасности путем сбора, обработки информации и выдачи ее на суда, оказание помощи в судовождении и организации движения объектов по акватории [1]. Она представляет собой сложную систему с разветвленной информационной частью и весьма сложными алгоритмами обработки информации, и состоит из следующих основных подсистем: сбора информации, дистанционного управления и передачи информации, обработки и отображения информации, связи и базы данных [2]. Каждая из подсистем представлена техническими средствами. Поэтому СУДС является совокупностью технических средств (ТС), организационных мер, персонала, зданий, сооружений.
Технические средства, как объект эксплуатации, представляют собой сложную техническую систему, состоящую из конструктивно оформленных элементов с разным уровнем надежности, и часто имеющих самостоятельное назначение, свои частные цели и задачи функционирования. В тоже время каждое из них выполняет функции непосредственно связанные с обеспечением безопасности мореплавания, сохранности человеческих жизней и обеспечением экологической безопасности, в связи с чем, к ним предъявляются высокие требования эксплуатационной надежности, под которой понимаем свойство технической системы непрерывно сохранять безопасное, работоспособное состояние, при котором она будет выполнять все функции, для достижения которых была построена, в течение определенного интервала времени, в заданных условиях эксплуатации при соблюдении установленных правилами технической эксплуатации мер технического обслуживания и текущего ремонта.
Этап эксплуатации технических средств играет особую роль в процессе жизненного цикла СУДС, поскольку все усилия, затраченные на создание высококачественной системы, могут быть сведены на «нет» неправильно или нерационально организованной эксплуатацией [3]. Следовательно, эксплуатация должна обеспечивать наибольшую эффективность функционирования технических средств, под которой понимаем количественный показатель надежности (коэффициент готовности), по которому можно во время функционирования судить об уровне достижения поставленных перед системой целей и задач. Поэтому проблема повышения уровня эксплуатационной надежности ТС СУДС в настоящее время является актуальной.
Одним из перспективных методов анализа эксплуатационной надежности ТС СУДС является логико-вероятностный метод (ЛВМ), математическая сущность которого заключается в использовании функций алгебры логики (ФАЛ) для аналитической записи условий работоспособности системы и в разработке строгих способов перехода от ФАЛ к вероятностным функциям (ВФ), объективно выражающим безотказность этой системы. Для перехода от ФАЛ к ВФ требуется преобразование логической функции, которое обеспечивает применение к ней основных теорем теории вероятностей. Логико-вероятностную теорию следует отличать от известной вероятностной логики, предметом которой является оценка истинности гипотез (высказываний), заключенных в промежутке между ложью и истиной. Реальные системы, к которым относятся ТС СУДС, описываются ФАЛ с повторными аргументами, отрицаниями аргументов, что не дает возможности напрямую пользоваться известными методами теории вероятностей. Поэтому проанализируем существующие алгоритмы перевода функции алгебры логики в вероятностную функцию при расчете эксплуатационной надежности.
Для практического применения при расчете эксплуатационной надежности ТС СУДС наиболее удобным являются алгоритмы ортогонализации, рекуррентный и наращивания путей, рассмотрим каждый из них более подробно.
Алгоритм ортогонализации основан на преобразовании ФАЛ в ортогональную дизъюнктивно-нормальную форму (ОДНФ).
Отрицание конъюнкции Ki можно представить в виде дизъюнкции:
члены которой попарно ортогональны [4]. Если в конъюнкции Ki отсутствуют отрицания, то отрицание ее можно представить в следующем виде:
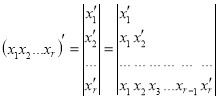 (1)
(1)
Булева функция f(z1, z2,..., zm), представленная в виде
![]() ,
,
эквивалентна функции ![]() . В матричном виде:
. В матричном виде:
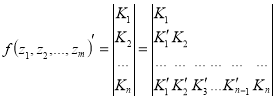 . (2)
. (2)
Если вместо каждого выражения ![]() подставить его представление, согласно (1), то в результате приведения функции к дизъюнктивно-нормальной форме (ДНФ) мы получим ОДНФ.
подставить его представление, согласно (1), то в результате приведения функции к дизъюнктивно-нормальной форме (ДНФ) мы получим ОДНФ.
Опишем кратко алгоритм ортогонализации:
-
Преобразовываем функцию
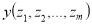 к ДНФ.
к ДНФ.
- Производим нумерацию членов ДНФ от 1 до n (n<2m), причем членам низшего ранга присваиваем низшие номера.
-
Определяем ОДНФ функции
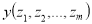 по (2).
по (2).
-
Для уменьшения числа операций целесообразно в конъюнкции
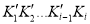 выполнить упрощения:
выполнить упрощения:
– прировнять к нулю те члены ДНФ ![]() , которые ортогональны члену Ki;
, которые ортогональны члену Ki;
– приравнять к нулю те элементарные конъюнкции отрицаний ![]() , которые ортогональны Ki.
, которые ортогональны Ki.
-
Вычислить вероятность опасности исходя из того, что все элементарные конъюнкции ортогональны, т. е. события несовместны:
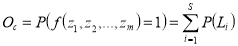 , где Li — ортогональные члены функции
, где Li — ортогональные члены функции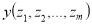 , записанные в ОДНФ.
, записанные в ОДНФ.
Рекуррентный алгоритмоснован на использовании теоремы сложения вероятностей совместных событий, в качестве которых здесь непосредственно выступают элементарные конъюнкции ДНФ, характеризующие опасные пути развития аварии.
Согласно правилам теории вероятностей, вероятность реализации опасного состояния системы при развитии аварии можно вычислить по формуле:
![]()
![]() .
.
Рекуррентно это выглядит следующим образом:
![]() ;
;
![]() ;
;
![]() ;
;
…
![]() .
.
При программировании этого алгоритма в памяти хранится информация лишь i-го шага, что существенно экономит ресурсы машины.
Содержание алгоритма наращивания путей заключается в следующем:
1. Функцию ![]() преобразовываем в ДНФ;
преобразовываем в ДНФ;
2. Нумеруем члены ДНФ от 1 до d (d < 2m), причем членам низшего ранга присваиваем низшие номера;
3. Преобразовываем эту ДНФ по формуле П. С. Порецкого [4]
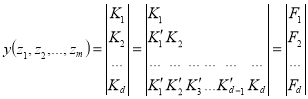 ,
,
где ![]() — логическая функция опасности реализации (i+1)-го пути развития аварии с учетом невозможности осуществления всех i-ых предшествующих путей.
— логическая функция опасности реализации (i+1)-го пути развития аварии с учетом невозможности осуществления всех i-ых предшествующих путей.
Все логические функции Fi ортогональны в совокупности, значит можно определить вероятностную функцию по формуле:
![]() .
.
При вычислении вероятности истинности функции Fi+1, т. е. P(Fi+1=1), ее следует понимать как условную вероятность невозможности всех предшествующих i-ых путей при условии, что элементы (i+1)-го пути на это не повлияли. Рекуррентно это можно представить следующим образом:
![]() ;
;
![]() ;
;
…
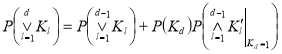 .
.
На основании закона двойственности [4]
 ,
,
имеем
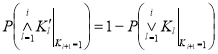 .
.
Поскольку существует много методов перевода ФАЛ в вероятностную функцию, то необходимо оценить известные алгоритмы с точки зрения трудоемкости вычислений и точности получаемого результата. При первоначальном рассмотрении исследуемой функции наиболее удобны в применении алгоритмы наращивания путей и рекуррентный, т. к. они не требуют дополнительных преобразований функции, представленной в ДНФ. В алгоритме наращивания путей необходима лишь перестановка элементарных конъюнкций в порядке возрастания их ранга. Алгоритм ортогонализации основан на преобразовании ФАЛ в ОДНФ с последующим применением теоремы о сумме вероятностей истинности попарно ортогональных функций алгебры логики. Он достаточно трудоемок, но с применением ЭВМ — это один из эффективных методов практических расчетов систем с большим числом элементов. Трудность в реализации на ЭВМ состоит в представлении ФАЛ в ОДНФ. Кроме того, этот алгоритм разрабатывался для работы с монотонными логическими функциями, а для расчетов с немонотонными ФАЛ требуется его адаптация.
Оценим трудоемкость каждого алгоритма с точки зрения зависимости количества производимых операций от количества элементарных конъюнкций, входящих в ФАЛ.
Пусть функция зависит от m аргументов, представлена в ДНФ и состоит из n элементарных конъюнкций Ki, каждая из которых содержит r1, r2,..., rn элементов.
В алгоритме ортогонализации функция представляется дизъюнкцией в базисе конъюнкция-отрицание элементарных конъюнкций Ki. Для этого необходимо пронумеровать входящие в нее конъюнкции в порядке возрастания их ранга. После чего выполнить n-1 вычисление конъюнкций Ki и их отрицаний. Для такой записи функции необходимо вычислить n-1 отрицание Ki и представить его в виде дизъюнкции в базисе конъюнкция-отрицание элементов. Т.о., количество предварительных операций равняется 2n-2. В итоге этих преобразований, функция оказывается в ОДНФ, количество конъюнкций которой зависит от конкретной задачи и максимально равно 1+r1+r1r2+r1r2r3+…+r1r2…rn, где ri — ранги элементарных конъюнкций [4]. Вычисление самой вероятности наступления события производится в одно действие.
Рекуррентный алгоритм в отличие от алгоритма ортогонализации или наращивания путей, не требует дополнительных преобразований функции. Он реализуется за n шагов. На первом шаге вычисляются вероятности каждой конъюнкции в ДНФ. На последующих шагах происходит рекуррентное вычисление вероятности наступления события. На последнем этапе мы получаем искомую вероятность, т. е. производится 2n-1 вычисления, из которых n вычисляется элементарно.
В начале алгоритма наращивания путей необходимо пронумеровать входящие в него конъюнкции в порядке возрастания их ранга. Алгоритм выполняется за n шагов: на первом шаге вычисляются вероятности каждой конъюнкции; на последующих шагах происходит рекуррентное вычисление вероятности наступления события; на последнем этапе получаем искомую вероятность. Каждый шаг, начиная со 2-го, состоит из двух этапов: подготовительного и непосредственного вычисления вероятности. При реализации этого алгоритма необходимо произвести 3n-2 вычислений. Преимущество этого алгоритма в сравнении с рекуррентным состоит в том, что при вычислении вероятности на i-ом шаге (i >1) используется условная вероятность невозможности всех предшествующих (i-1) путей при условии, что элементы i-го пути на это не повлияли. Следовательно, в конъюнкциях вместо переменных, входящих в i-ый путь, стоят 1, что существенно облегчает вычисления.
При расчетах эксплуатационной надежности ТС СУДС рациональнее всего было бы использовать рекуррентный алгоритм, т. к. он требует наименьшее число вычислений. Это действительно так, если значения вероятностей возникновения исходных событий достаточно точны, тогда при их умножении не возникнет большой погрешности. В противном случае удобным оказывается алгоритм наращивания путей, т. к. за счет использования условных вероятностей некоторые переменные заменяются единицей, а значит, при умножении не влияют на результат. Лучше всего в случае, когда вероятности найдены приближенно, использовать алгоритм ортогонализации, т. к., во-первых, вероятность там вычисляется один раз в конце, а, во-вторых, вероятности складываются и суммарная погрешность меньше. Но, как сказано выше, этот алгоритм требует корректировки для работы с немонотонными функциями.
Проанализировав существующие алгоритмы перевода функции алгебры логики в вероятностную функцию при расчете эксплуатационной надежности ТС СУДС, необходимо отметить, что для программной реализации удобнее всего использовать рекуррентный алгоритм, являющийся приемлемым компромиссом между простотой в использовании и погрешностью результата.
Литература:
- Приказ Министерства транспорта РФ от 23 июля 2015г. № 226 «Об утверждении Требований к радиолокационным системам управления движением судов, объектам инфраструктуры морского порта, необходимым для функционирования Глобальной морской системы связи при бедствии и для обеспечения безопасности, объектам и средствам автоматической информационной системы, службе контроля судоходства и управления судоходством».
- Тюфанова, А. А. Методика анализа эксплуатационной надежности технических средств системы управления движением судов на примере порта Новороссийск/ А. А. Тюфанова. — Казань: Изд-во «Бук», 2015. — 104 C.
- Тюфанова, А. А. Анализ факторов, влияющих на эксплуатационную надежность технических средств системы управления движением судов// Надежность № 4 (55) — М: ООО «Издательский дом «Технологии»", 2015.
- Горопашная, А. В. Методы анализа безопасности сложных технических систем. Автореферат дис…кан. физ.-мат. наук.: СПб, 2009.
Ключевые слова
алгоритм, технические средства, функция алгебры логики, система управления движени-ем судовПохожие статьи
Разработка алгоритма для управляющих действий боковым движением самолета при заходе на взлетно-посадочную полосу
В статье приводятся принципы составления правил логического вывода для нечеткой системы автоматического управления боковым движением самолета при заходе на взлетно-посадочную полосу. Разработан алгоритм (закон) управления (для управляющих действий) б...
Методы математического программирования при разработке автоматизированных систем управления деятельностью авиакомпаний и аэропортов
В статье авторы поднимают вопрос необходимости разработки автоматизированных систем управления деятельностью авиакомпаний и аэропортов, рассматривают методы математического программирования применительно к деятельности авиакомпаний и аэропортов.
Визуализация математических имитационных сетевых моделей ГТД в системе моделирования DVIG
В работе рассмотрен способ представления и получения геометрического потока в системе имитационного моделирования ГТД DVIGw. Показана актуальность применения данного потока и способы развития системы в данном направлении, а также создана модель ТРДД ...
К вопросу оценки качества функционирования дизельной энергетической установки автономных локомотивов
В статье рассмотрен подход к выбору оптимального множества параметров контроля качества функционирования дизельной энергетической установки. Подход основан на разработке и анализе математических моделей ее функциональных подсистем, представленных гра...
Анализ методических подходов к оценке эффективности эксплуатации морского транспортного флота
В работе рассмотрены различные подходы к оценке эффективности эксплуатации морского транспортного флота. Определяется взаимосвязь эффективности работы флота и морских портов. Раскрывается эффективность использования информационных технологий, влияющи...
Совершенствование построения теоретических моделей надежности газонефтепроводов
Создана новая методика построения модели надежности газонефтепроводов с помощью объектно-ориентированного языка программирования C# (Си Шарп), в частности, использование библиотеки C # для вычислений нейронных сетей и их применение для решения задач ...
Применение генератора колебаний с хаотической несущей в технических средствах системы управления движением судов
Рассмотрена возможность применения генератора колебаний с хаотической не-сущей в технических средствах системы управления движением судов.
Исследование и разработка модели оценки информационной безопасности объекта
В статье проведен анализ качественного, количественного и комплексного подходов для минимизации угрозы информационной безопасности, выбран наилучший. На основании проведенного анализа строится математическая модель и алгоритм модели оценки информацио...
Формирование алгоритма автоматизации работы системы доставки нефтепродуктов на АЗС
Данная статья посвящена проблеме повышения эффективности системы доставки нефтепродуктов на автозаправочные станции внутри одного региона. Для этого в данной статье рассматривается существующая система доставки нефтепродуктов на АЗС. Выделяются инфор...
Компьютерное моделирование в реальном времени движения автомобильного колеса в тормозном режиме с применением элементов нечеткой логики
В статье рассматриваются проблемы адекватности моделей динамических процессов в реальном времени на примере моделирования антиблокировочной системы тормозов автомобиля. Производится реализация нечеткого моделирования в задачах автомобильного транспор...
Похожие статьи
Разработка алгоритма для управляющих действий боковым движением самолета при заходе на взлетно-посадочную полосу
В статье приводятся принципы составления правил логического вывода для нечеткой системы автоматического управления боковым движением самолета при заходе на взлетно-посадочную полосу. Разработан алгоритм (закон) управления (для управляющих действий) б...
Методы математического программирования при разработке автоматизированных систем управления деятельностью авиакомпаний и аэропортов
В статье авторы поднимают вопрос необходимости разработки автоматизированных систем управления деятельностью авиакомпаний и аэропортов, рассматривают методы математического программирования применительно к деятельности авиакомпаний и аэропортов.
Визуализация математических имитационных сетевых моделей ГТД в системе моделирования DVIG
В работе рассмотрен способ представления и получения геометрического потока в системе имитационного моделирования ГТД DVIGw. Показана актуальность применения данного потока и способы развития системы в данном направлении, а также создана модель ТРДД ...
К вопросу оценки качества функционирования дизельной энергетической установки автономных локомотивов
В статье рассмотрен подход к выбору оптимального множества параметров контроля качества функционирования дизельной энергетической установки. Подход основан на разработке и анализе математических моделей ее функциональных подсистем, представленных гра...
Анализ методических подходов к оценке эффективности эксплуатации морского транспортного флота
В работе рассмотрены различные подходы к оценке эффективности эксплуатации морского транспортного флота. Определяется взаимосвязь эффективности работы флота и морских портов. Раскрывается эффективность использования информационных технологий, влияющи...
Совершенствование построения теоретических моделей надежности газонефтепроводов
Создана новая методика построения модели надежности газонефтепроводов с помощью объектно-ориентированного языка программирования C# (Си Шарп), в частности, использование библиотеки C # для вычислений нейронных сетей и их применение для решения задач ...
Применение генератора колебаний с хаотической несущей в технических средствах системы управления движением судов
Рассмотрена возможность применения генератора колебаний с хаотической не-сущей в технических средствах системы управления движением судов.
Исследование и разработка модели оценки информационной безопасности объекта
В статье проведен анализ качественного, количественного и комплексного подходов для минимизации угрозы информационной безопасности, выбран наилучший. На основании проведенного анализа строится математическая модель и алгоритм модели оценки информацио...
Формирование алгоритма автоматизации работы системы доставки нефтепродуктов на АЗС
Данная статья посвящена проблеме повышения эффективности системы доставки нефтепродуктов на автозаправочные станции внутри одного региона. Для этого в данной статье рассматривается существующая система доставки нефтепродуктов на АЗС. Выделяются инфор...
Компьютерное моделирование в реальном времени движения автомобильного колеса в тормозном режиме с применением элементов нечеткой логики
В статье рассматриваются проблемы адекватности моделей динамических процессов в реальном времени на примере моделирования антиблокировочной системы тормозов автомобиля. Производится реализация нечеткого моделирования в задачах автомобильного транспор...











