В статье рассматриваются проблемы адекватности моделей динамических процессов в реальном времени на примере моделирования антиблокировочной системы тормозов автомобиля. Производится реализация нечеткого моделирования в задачах автомобильного транспорта применительно к антиблокировочной системе тормозов автомобиля.
Ключевые слова : адекватность модели, динамическая система, компьютерное моделирование, ABS, нечеткая логика.
В настоящее время достаточно сложной задачей является моделирование динамических систем в реальном времени. Обычно, такие моделирования подразумевают наиболее точное описание процесса с нелинейными характеристиками и использование некоторого количества параметров, изменяющихся с течением времени. Также создание адекватной модели динамической системы в реальном времени подразумевает решение ряда проблем.
Главной задачей работы антиблокировочной системы тормозов (ABS) автомобиля является сохранение устойчивости и управляемости во время торможения. Основные входные данные для расчёта ключевых параметров — линейная скорость и ускорение автомобиля, а также угловая скорость и ускорение колеса. Ключевые параметры, которые определяют работу системы ABS, являются коэффициент продольного сцепления колеса с поверхностью дороги φ и коэффициент продольного проскальзывания S. Для того, чтобы определить угловую скорость колеса, используют в основном импульсные магнитные датчики. Определение линейной скорости транспортного средства имеет несколько способов, которые основаны на: обработке сигналов датчика частоты вращения выходного вала КПП; одновременной обработке сигналов нескольких датчиков угловой скорости колес автомобиля. Полученные данные позволяют программному обеспечению блока управления антиблокировочной тормозной системы (ECU ABS) осуществлять распределение тормозных усилий. Эффективность антиблокировочной системы тормозов определяется двумя факторами: погрешностью показаний датчиков в системе; адекватностью процесса обработки входных данных вычислительным устройством [1].
Модели, которые предполагают решение дифференциальных уравнений, нуждаются в значительных затратах машинного времени, необходимого для расчета моделируемых процессов, что является очень важным при расчетах в режиме реального времени. Уменьшение шага интегрирования позволяет повысить точность вычислений, но при этом возрастает время счета. На практике использование таких численных методов, как, например, Рунге-Кутты IV-го порядка, позволяет лишь отчасти решить проблему недостатка вычислительных мощностей. Проблему повышения скорости счета можно решить за счет использования более производительного вычислительного элемента ЭБУ, но это приведет к подорожанию ЭБУ. Одним из возможных методов представления модели процесса торможения колеса в реальном времени с учетом прилагаемых тормозных усилий и позволяющий исключить системы дифференциальных уравнений, как промежуточный этап вычислений, является метод нечеткой логики с использованием лингвистических переменных. Использование лингвистических переменных, которые применяются в нечеткой логике, потребуют значительно меньшей мощности вычислительного элемента ЭБУ.
Наибольшее распространение аппарат нечеткой логики получил в теории автоматического управления. К построению моделей, основанных на нечеткой логике, прибегают в том случае, когда предмет исследования имеет слабую формализацию и его точное математическое описание слишком сложное или неизвестно. Сложность точного математического описания процессов при торможении автомобильного колеса в реальном времени определяет выбор данного метода. Теорема о нечеткой аппроксимации, которая была доказана в 1992 г. Б.Коско, гласит, что любая математическая система может быть аппроксимирована системой на нечеткой логике. Как следствие, с использованием естественно-языковых высказываний «если-то» с последующей их формализацией средствами теории нечетких множеств без использования сложного аппарата дифференциального и интегрального исчислений можно сколь угодно точно отобразить произвольную связь «входы-выход». Так как нечеткие модели хорошо зарекомендовали себя в использовании при решении задач оптимизации в режиме реального времени, применение их в моделировании антиблокировочной системы тормозов автомобиля видится эффективным, перспективным и обоснованным.
Рассмотрим модель колеса в режиме торможения (рис. 1).
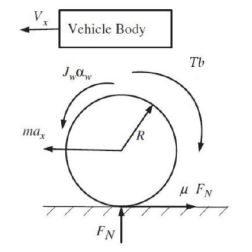
Рис. 1. Динамическая модель колеса транспортного средства
При построении описания системы ABS произведем следующие допущения:
– масса автомобиля равномерно распределена по всем четырем колесам;
– влияние подвески и трансмиссии автомобиля не учитывается;
– динамика колес автомобиля идентична.
Опишем колесо в режиме торможения системой уравнений:
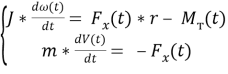
При этом:
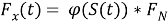
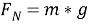
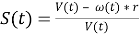

где:
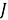
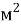
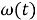
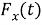
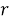
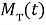
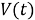
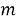
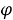
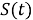
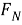
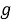
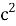
Отсюда выразим:
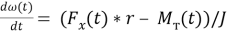
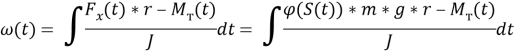
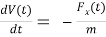
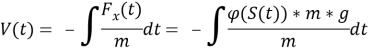
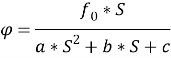
Промоделируем все это в MATLAB Simulink.
![Формула [1]](https://articles-static-cdn.moluch.org/articles/j/81020/images/81020.025.png)
Рис. 2. Формула
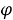
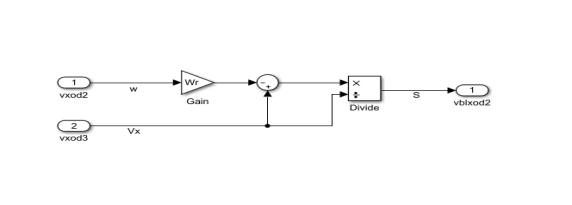
Рис. 3. Формула продольного проскальзывания S колеса
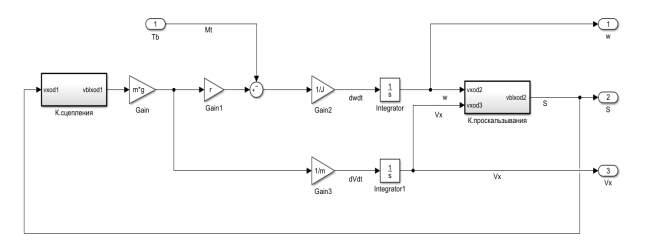
Рис. 4. Динамическая модель колеса транспортного средства
Теперь используем библиотеку Fuzzy Logic Toolbox пакета MATLAB. Необходимо определиться с количеством входных и выходных переменных, базой правил, методом нечеткого логического вывода и методом дефаззификации [2].
В нашей модели будет две входные переменные: продольное проскальзывания колеса S и скорость автомобиля V; одна выходная переменная: давление в тормозной системе p a ; логический вывод Мамдани; дефаззификация по методу центра тяжести.
Введем функции принадлежности для входных и выходной переменных.

Рис. 5. Функция принадлежности продольного проскальзывания S колеса
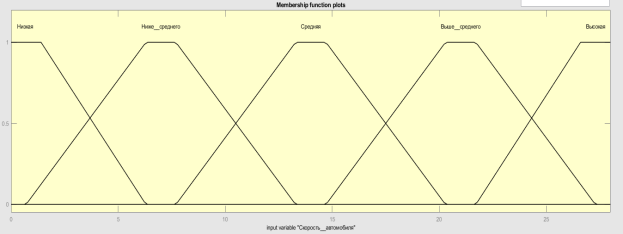
Рис. 6. Функция принадлежности скорости автомобиля V
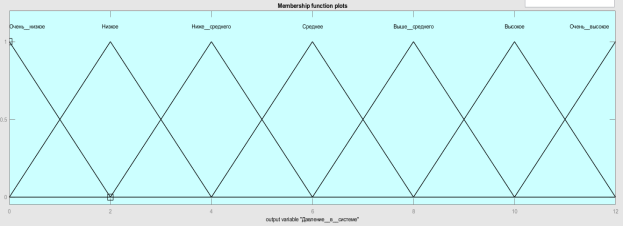
Рис. 7. Функция принадлежности давления в тормозной системе p a
Включим нечеткий регулятор в подсистему одноколесной модели ABS.
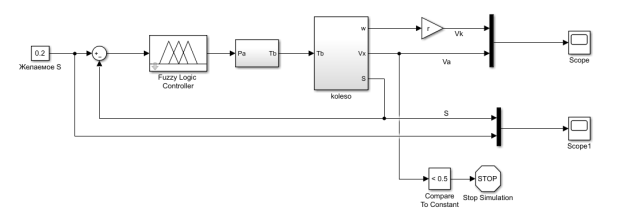
Рис. 8. Реализация в MATLAB Simulink одноколесной модели ABS под управлением нечеткого регулятора
Эксперимент произведем при значениях: начальная скорость
V
= 27.78 м/с (100 км/ч); момент инерции колеса
J
= 1.1 кг∙
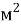
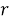
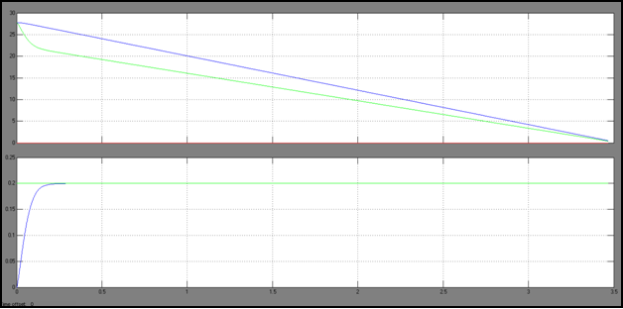
Рис. 9. Изменение скоростей и продольного проскальзывания при торможении
Полученные результаты продемонстрировали адекватность формулы Ревина для коэффициента сцепления [1] реальному процессу. Это дает основание использовать в дальнейшем ее в модели АБС автомобиля.
Вывод:
Использование нечеткой логики в моделировании позволяет приблизить построение модели к человеческому восприятию. Также нечеткое моделирование дает возможность снизить необходимость в значительных вычислительных мощностях на промежуточные вычисления, которые связаны с динамическими параметрами. Все это позволит обрабатывать входные данные с требуемым уровнем точности в динамических процессах в реальном времени. Но при этом также и выходные данные после обработки будут обладать высокой точностью соответствия характеристикам реальных процессов. К месту будет привести замечание основателя нечеткой логики Лотфи Заде, который говорил, что «почти всегда можно сделать такой же самый продукт без нечеткой логики, но с нечеткой будет быстрее и дешевле» [2]. На основании всего вышеперечисленного можно говорить о повышении адекватности в моделях динамических процессов в реальном времени благодаря нечеткому моделированию.
Литература:
- Балакина Е. В., Зотов Н. М., Платонов, Федин А. П. Проблемы моделирования динамических процессов в реальном времени. Волгоград, 2013.
- Пегат А. Нечеткое моделирование и управление, пер. с английского А. Г. Подвесовского, Ю. В. Тюменцева. М.: БИНОМ. Лаборатория знаний, 2013.
- Писаренко А. В., Белоус А. В., Кононенко Д. В. Компьютерное моделирование поведения транспортного средства с антиблокировочной системой. Збiрник наукових праць Харкiвського унiверситету Повiтряних Сил, 2013.
- Федин А. П. Обеспечение адекватности моделирования рабочих процессов элементов автомобиля при испытаниях на виртуально-физических стендах-тренажерах. — Диссертация на соискание степени канд. техн. наук / А. П. Федин. — Волгоград, 2006. 944
- Штовба С. Д. Проектирование нечетких систем средствами MATLAB / С. Д. Штовба. — М.: Горячая линия — Телеком. — 2007. — 288 с.
- Aksjonov A. Design and Simulation of the Robust ABS and ESP Fuzzy Logic Controller [Электронный ресурс] / Aksjonov A., Augsburg K. // Applied Sciences. — 2016. — 6(12). — Режим доступа: http://www.mdpi.com/2076- 3417/6/12/382.
- Kant Abhinav. Enhanced Antilock Braking System using Fuzzy Logic Road Detector / Kant Abhinav, Mukesh Kumar // International Journal of Research in Electrical & Electronics Engineering. — 2013. — Vol. 1. — № 2. — p. 47–54.

