Накопление случайности в генераторах псевдослучайных чисел

В статье автор рассказывает о накоплении случайности в генераторах псевдослучайных чисел и приводит результаты экспериментов, подтверждающих факт возможности накопления случайностей.

Ключевые слова: ГПСЧ, накопление случайности, псевдослучайное число, XOR.

Случайными числами называют последовательность чисел, которая составлена из чисел определенного диапазона, между которыми нет никакой статистической и математической зависимости, и подчиняется какому-либо закону распределения. При идеальной генерации случайных чисел вероятность «выпадения» у всех чисел диапазона одинакова и определяется по формуле вероятности:

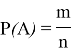
где: m — количество способов, которыми может выпасть конкретное число из диапазона, n — всего чисел в диапазоне.

В вычислительной технике случайностей нет и генерировать случайные числа она не может. Однако компьютеры могут создавать числа, которые выглядят случайными, но таковыми не являются. Такие числа называются псевдослучайными, а их генераторы — генераторами псевдослучайных чисел (ГПСЧ). Простыми примерами ГПСЧ могут служить метод «середины квадрата» [1] и линейный конгруэнтный метод [2].

Больше всего в случайных числах нуждается криптография — наука о шифровании (защиты информации). Любой алгоритм шифрования использует ключ — псевдослучайное секретное число, позволяющее зашифровать и расшифровать данные. Случайность таких чисел должна быть очень высока, а их размер, на сегодняшний день, не менее 128 бит. [3] Почти все ГПСЧ не могут быть использованы в области криптографии из-за малой случайности. При этом о возможности накопления этими генераторами случайности до необходимого уровня в какой-либо литературе и научных работах не говорится (автор таких книг и научных работ не нашел).

«Неслучайность» (Q) при генерации мыслится мной как разница вероятностей появления наиболее вероятного и наименее вероятного числа:

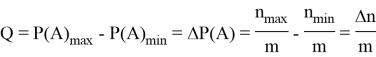
где: Q — неслучайность ГПСЧ, P(A) _max — вероятность наиболее вероятного числа, P(A) _min — вероятность наименее вероятного числа, n _{max —} количество появлений наиболее вероятного числа, n _{min —} количество появлений наименее вероятного числа, m — количество генерируемых чисел всего.

Чем меньше Q, тем более случайные генерируются числа. Таким образом, случайность генератора чисел (S) вычисляется по формуле:

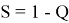
Кроме случайности, у ГПСЧ, есть еще один параметр — энтропия. Несмотря на взаимосвязь случайности и энтропии, вторая никак не влияет на первую, поэтому в данной работе рассматриваться не будет. [4] [5]

В 1917 году Гилберт Вернам изобрел невзламываемый шифр (шифр Вернама). Реализуется он при помощи логической функции ⊕ («сложение по модулю 2», «исключающее или», XOR). Дело в том, что в результате применения ⊕ к тексту и ключу (случайному числу) побитно, получается абсолютно случайная последовательность неподдающаяся какому-либо анализу и взлому. [5] Можно сказать, что при помощи ⊕ сообщение «наделяется» той хаотичностью и случайностью, которой обладает ее ключ. Именно таким образом можно «накапливать» случайность в генераторах псевдослучайных чисел, приближая случайность создаваемых им чисел к идеальной. Формулой это можно выразить так:

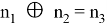
где: n _1– 1 псевдослучайное число, n _2– 2 псевдослучайное число, n _3– 3 псевдослучайное число, более случайное, чем n ₁ и n _2.

Приведем пример: генератор псевдослучайных чисел сгенерировал псевдослучайное число n ₁ . Случайность этого числа можно увеличить, сгенерировав псевдослучайное число n ₂ и применив к ним ⊕ побитно.

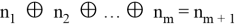
Для доказательства теоремы был проведен следующий эксперимент: 4 различных ГПСЧ по 9 раз генерировали 1 миллион псевдослучайных чисел от 0 до 9. Первый миллион чисел генерировался без сложения по модулю два с другими псевдослучайными числами. Второй миллион чисел генерировался с 1 сложением по модулю 2 с другим псевдослучайным числом, созданным этим же генератором. Последующие генерации производились с увеличением числа сложений по модулю 2 в 2 раза. Далее были вычислены по каждому миллиону чисел P(A) _max , P(A) _min и Q. Для проведения эксперимента были выбраны следующие ГПСЧ: «rand» [6], «random_int» [7], «random_bytes» [8], и «openssl_random_pseudo_bytes» [9]. Результаты эксперимента представлены в таблицах 1 и 2.

Таблица 1

Результаты экспериментов на ГПСЧ rand и random _ int

Таблица 2

Результаты экспериментов с ГПСЧ random_bytes и openssl_random_pseudo_bytes

Выводы:

1. Накапливать случайность ГПСЧ возможно путем сложения по модулю 2 с другими случайными числами.
2. Максимально возможная случайность (S) любого ГПСЧ 0,9999≤S<1 (0
3. Если ГПСЧ имеет случайность (S) в диапазоне 0,9999≤S<1 (0
4. У некоторых ГПСЧ при первом сложении по модулю 2 случайность генерируемых чисел может уменьшиться, но она возрастает при дальнейшем накоплении при помощи ⊕.
5. ГПСЧ с низкой случайностью можно использовать в криптографии при условии накопления ими случайности.

Литература:

1. Von, Neumann. Various techniques used in connection with random digits. / Neumann Von, John.. — Текст: непосредственный // National Bureau of Standards Applied Mathematics Series.. — 1951. — № 12. — С. 36–38.
2. Маккафри, Д. Тесты — Упрощенная генерация случайных чисел. / Д. Маккафри. — Текст: электронный // Microsoft.: [сайт]. — URL: https://docs.microsoft.com/ru-ru/archive/msdn-magazine/2016/august/test-run-lightweight-random-number-generation (дата обращения: 04.02.2022).
3. A. Biryukov, D. Khovratovich. Related-key Cryptanalysis of the Full AES-192 and AES-256. / A. Biryukov, D. Khovratovich. — Текст: электронный // impic.org: [электронный документ]. — URL: http://www.impic.org/papers/Aes-192–256.pdf (дата обращения: 04.02.2022).
4. Shannon, C. E. A Mathematical Theory of Communication / C. E. Shannon. — Текст: непосредственный // Bell System Technical Journal. — 1948. — № 27. — С. 379–423.
5. Shannon, C. E. Communication Theory of Secrecy Systems / C. E. Shannon. — Текст: непосредственный // Bell System Technical Journal. — 1949. — № 28. — С. 656–715.
6. rand. — Текст: электронный // php.net: [сайт]. — URL: https://www.php.net/manual/ru/function.rand.php (дата обращения: 07.02.2022).
7. random_int. — Текст: электронный // php.net: [сайт]. — URL: https://www.php.net/manual/ru/function.random-int.php (дата обращения: 07.02.2022).
8. random_bytes. — Текст: электронный // php.net: [сайт]. — URL: https://www.php.net/manual/ru/function.random-bytes.php (дата обращения: 07.02.2022).
9. openssl_random_pseudo_bytes. — Текст: электронный // php.net: [сайт]. — URL: https://www.php.net/manual/ru/function.openssl-random-pseudo-bytes.php (дата обращения: 07.02.2022).