В статье приводятся задачи теории вероятностей, в решении которых возникают классические константы π и e. Показана вероятностная интерпретация теоремы Дирихле-Вирзинга о приближении действительных чисел алгебраическими числами.

Ключевые слова: алгебраические числа, диофантовы приближения, распределениеалгебраических чисел, вероятность, числоπ, числоe.

Известны несколько вероятностных задач, в которых возникают классические константы, например и . Приведём примеры.

Пример 1. Задача Бюффона. На плоскости нарисованы параллельные прямые на одинаковом расстоянии друг от друга. На плоскость бросается игла длины (). Найти вероятность того, что игла пересечет какую-нибудь прямую.

Эта задача на геометрическую вероятность. Обозначим через расстояние от середины иглы до ближайшей параллельной прямой и через — угол между иглой и прямой (рисунок 1).

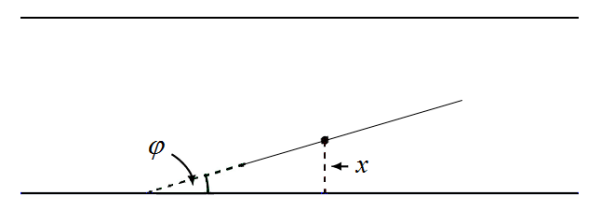
Рис. 1

Радианная мера угла меняется от 0 до π. Расстояние принимает значения от 0, если середина иголки попала на прямую, до . На плоскости с координатами эти ограничения задают прямоугольник (рисунок 2).

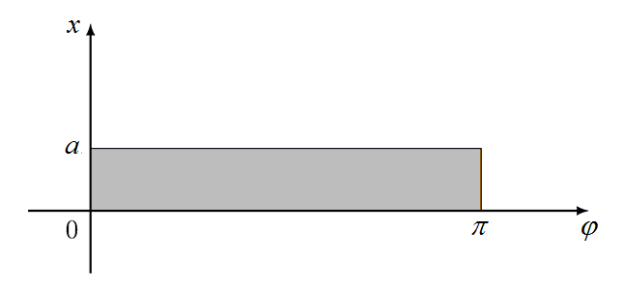
Рис. 2

Из рисунка 3 видно, что иголка пересекает хотя бы одну прямую, если x будет меньше проекции половины иголки на направление, перпендикулярное прямым.

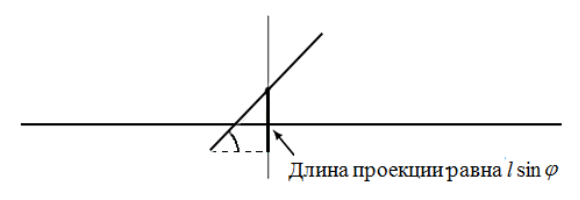
Рис. 3

Условие пересечения имеет вид . Искомая вероятность равна отношению площади под синусоидой к площади всего прямоугольника (рисунок 4)

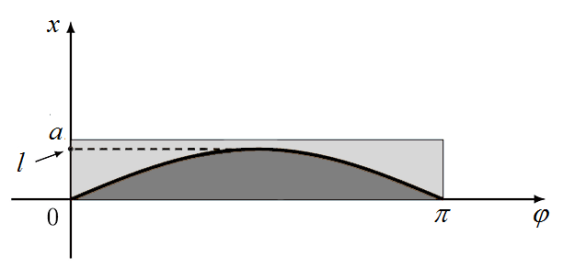
Рис. 4

Вероятность может быть найдена по формуле:

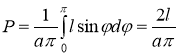(1)

По закону больших чисел , где — частота, с которой происходит искомое событие. Отсюда (1) принимает вид и . Проделав эксперимент достаточно большое количество раз, мы можем вычислить . В известных нам экспериментах было равно 5000 и было определено с точностью до третьего знака после запятой.

Пример 2. Для выпечки булочек с изюмом было использовано изюминок. При каком значении в наудачу выбранной булочке окажется хотя бы одна изюминка?

Пусть — искомое событие. Тогда

,(2)

где — случайное событие, состоящее в том, что — я изюминка не попадет в данную булочку. Ясно, что .

Из (2) имеем

.

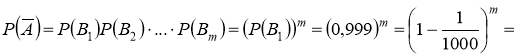
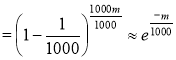Если 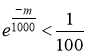, то

Осталось найти такое , что 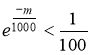.Для этого достаточно взять , т. е. изюминок должно быть в 5 раз больше чем булочек.

Для решения задачи мы использовали равенство при малых значениях λ.

Покажем, как с помощью вероятных соображений можно интерпретировать классические теоремы в теории диофантовых приближений, например, теорему Дирихле-Вирзинга о приближении действительных чисел алгебраическими числами.

Пусть x — действительное число и α алгебраическое число степени n и высоты . Высота алгебраического числа равна модулю максимального коэффициента минимального многочлена алгебраического числа. Пусть — многочлен с целыми коэффициентами степени . Обозначим через высоту многочлена, равную модулю максимального коэффициента многочлена .

При рассмотрим класс многочленов

.

Какой величины должна быть длина интервала , чтобы с вероятностью сколь угодно близкой к единице действительное алгебраическое число попало в интервал .

Обозначим длину интервала . Нетрудно доказать, что количество алгебраических чисел таких, что не менее . Занумеруем их . Пусть — искомое событие. Тогда , где — случайное событие, состоящее в том, что алгебраическое число не попало в интервал . Ясно, что .

Если и , то и . Следовательно, длина интервала .

Литература:

1. Шмидт В. М. Диофантовы приближения. — М.: Мир, 1983. — 232 с.
2. Касселс Дж. В. С. Введение в теорию диофантовых приближений. — М.: Изд-во иностр. лит-ры, 1961. — 213 с.
3. V. Beresnevich, V. Bernik, D. Kleinbock, G. Margulis. Metric diophantine approximation: The Khintchine-Groshev theorem for nondegenerate manifolds // Mosc. Math. J.. — Moscow. — № 2. — С. 203–225.