Метод обнаружения аномалий во временных рядах



В статье автор предлагает модернизированный метод экстремального студентизированного отклонения для обнаружения аномалий во временных рядах.

Ключевые слова: STL, временный ряд, ESD, данные, кусочно-линейная медиана, MAD.

Предлагается метод обнаружения аномалий в долгосрочных облачных данных, основанный на обобщенном алгоритме экстремального студентизированного отклонения (ESD), использующий кусочную аппроксимацию, лежащая в основе долгосрочной тенденции к минимизации количества ложно-положительных результатов, учитывающий как внутридневные так и/или еженедельные сезонные колебания, чтобы свести к минимуму количество ложных срабатываний.

Предлагаемый метод может быть использован для автоматического обнаружения аномалий в данных временных рядов для таких показателей работы приложения, как количество запросов в секунду (RPS), так и системных показателей, таких как загрузка процессора и тому подобных метрик, получаемых из системы мониторинга.

Также представлена подробная оценка предложенной техники с использованием данных с высоко-нагруженных продуктивных систем.

Учитывая скорость, объём и характер данных о облачных системам, генерируемых в режиме реального времени, нецелесообразно получать данные временных рядов с «истинными» аномалиями. Для этого случайным образом вводились аномалии в нормальные данные. Оценена эффективность предложенных методов в отношении обнаружения введённых аномалий.

Пусть Xt — наблюдение в момент времени t, где t = 0, 1, 2,..., а X обозначает набор всех наблюдений, составляющих временной ряд. Разложение временного ряда — это метод, который делит временной ряд (X) на три компонента, например, сезонный (SX), трендовый (TX) и остаточный (RX). Сезонная составляющая описывает периодические колебания временного ряда, в то время как трендовая составляющая описывает «вековые колебания» временного ряда, то есть долгосрочные непериодические колебания. Остаточная составляющая определяется как остаток временного ряда после удаления сезонности и тренда:

RX = X — SX — TX.

В случае долгосрочных аномалий необходимо с осторожностью определять компонент тренда, в противном случае наличие тренда может привести к появлению искусственных аномалий во временном ряду. Хорошо известно, что среднее значение выборки x̄ и стандартное отклонение (используемые в тестах на обнаружение аномалий, таких как ESD) по своей природе чувствительны к наличию аномалий во входных данных. Искажение среднего значения выборки увеличивается по мере того, как Xt → ±∞. Предлагаемый метод использует надежную статистику, такую как медиана, которая защищает от таких аномалий (медиана выборки может указывать на то, что до 50 % данных являются аномальными). Кроме того, предлагаемый метод использует среднее абсолютное отклонение (MAD), в отличие от стандартного отклонения, которое используется в изначальном методе ESD, поскольку он также устойчив при наличии аномалий во вводимых данных. MAD определяется как медиана абсолютных отклонений от медианы выборки.

MAD = медиана (Xi − медиана j (X j)).

Данные мониторинга демонстрируют как сезонность, так и скрытую тенденцию, которые оказывают негативные эффекты, приводящие к обнаружению ложных аномалий.

На основе производственных данных замечено, что основной тренд часто становится заметным, если интервал временного ряда превышает две недели. В таких случаях тренд вызывает изменение среднего значения от одного (дневного/недельного) цикла к другому. Это ограничивает комплексное выявление аномалий в долгосрочных временных рядах.

Рис. 1. STL (а) по сравнению с вариантом STL (б) декомпозиции

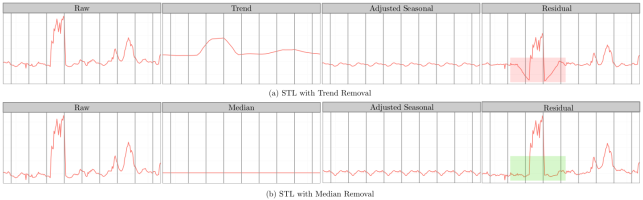
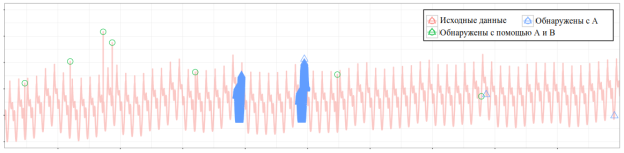
Разложение временных рядов облегчает фильтрацию тренда из необработанных данных. Однако получение тренда с помощью алгоритмов разложения временных рядов, таких как классический или STL (декомпозиция по сезонным трендам с помощью LOESS [3] (локально оцениваемое сглаживание разброса)), очень чувствительно к наличию аномалий во входных данных и, скорее всего, приведёт к появлению искусственных аномалий в остаточном компоненте после разложения. Это иллюстрирует отрицательная аномалия в остаточном компоненте, выделенная красным прямоугольником на рисунке 1 (a). Замена разложенного компонента тренда на медиану исходных данных временного ряда смягчает обозначенный выше эффект, устраняет появление фантомных аномалий, как показано зелёным прямоугольником на рисунке 1 (b). Хотя использование медианы в качестве замены тренда хорошо работает там, где наблюдаемый компонент тренда относительно прямолинейный, из практики замечено, что в случае долгосрочных временных рядов, где базовый тренд очень выражен, такой подход работает плохо. Было изучено два альтернативных подхода к выделению трендовой составляющей долгосрочного временного ряда: тренд STL и квантильная регрессия. Ни один из этих двух подходов не подходил для текущей задачи. Поэтому был предложен метод, названный кусочно-линейной медианой.

STL удаляет предполагаемую составляющую тренда из временного ряда, а затем разбивает данные на подциклы. Каждый подцикл состоит из значений в каждой точке сезонного цикла. Например, если временной ряд состоит из ежемесячных значений с годовой периодичностью, то первый подцикл состоит из значений за январь, второй — из значений за февраль и так далее.

LOESS сглаживает каждый ряд данных по подциклам для выделение сезонности. Такое разбиение рядов данных по подциклам позволяет декомпозировать более сложные функции, чем при классическом аддитивном или мультипликативном подходе.

Рис. 2. Иллюстрация тенденций, полученных с использованием различных подходов

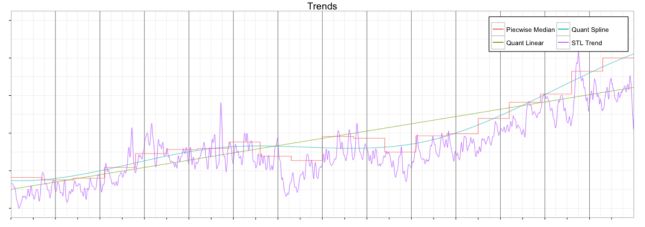
Затем из исходных данных временного ряда вычитается предполагаемый сезонный компонент; оставшаяся разница сглаживается с помощью LOESS, в результате чего получается предполагаемый компонент тренда. STL повторяет этот процесс, используя самый последний предполагаемый тренд, до тех пор, пока не достигнет сходимости разложения или пока разница в итерациях не станет меньше заданного порога. Фиолетовая линия на рисунке 2 иллюстрирует тренд, полученный с помощью STL.

В то время как регрессия методом наименьших квадратов пытается подогнать среднее значение зависимой переменной, квантильная регрессия пытается подогнать медиану или другие квантили. Это обеспечивает статистическую устойчивость к наличию аномалий в данных. Сочетание этого метода с B-сплайном оказалось эффективным способом оценки нелинейных трендов во временных рядах, которые охватывают более двух недель. Это позволяет хорошо выявлять основные тенденции в долгосрочных временных рядах. Однако замечено, что, если временной ряд имеет длинну две недели или меньше, то нарушается соответствие тренду. Это означет, что большие блоки аномалий искажали сплайн и приводили к большому количеству ложноотрицательных результатов (FN) и ложноположительные срабатывания (FP). Вышеупомянутый провал в двухнедельных периодах означает, что квантильный B-сплайн неприменим в кусочном виде, и, как таковой, является дополнительной мотивацией для использования кусочно-медианного подхода. Кроме того, на рисунке 2 мы видим, что линейная квантильная модель, показанная зелёной линией, также плохо соответствует долгосрочному тренду.

Чтобы устранить ограничения, упомянутые выше, предлагается аппроксимировать базовый тренд в долгосрочном временном ряду с помощью кусочно-линейного метода. В частности, тренд вычисляется как кусочно-линейная комбинация краткосрочных медиан. На основе эксперимента с использованием производственных данных замечено, что стабильные показатели обычно демонстрируют незначительное изменение медианы в течение двухнедельных периодов.

Эти медианные значения за две недели дают достаточно точек данных для анализа сезонности, а также служат базовой линией для выявления аномалий. Красная линия на рисунке 2 иллюстрирует тенденцию, полученную с помощью кусочно-линейного подхода.

Далее представлено формальное описание предлагаемого метода. Алгоритм имеет два входных параметра: временной ряд X и максимальное количество аномалий k.

Алгоритм обнаружения аномалий, таким образом, можно описать как:

1. определяется периодичность/сезонность;
2. X разбивается на непересекающиеся окна WX (t), длинной не менн двух недель

for all WX (t) do

Require:

nW = количество наблюдений в WX (t)

k ≤ (nW × 0,49)

3. Извлечение сезонной SX компоненты с использованием STL
4. Вычисление медианы X̃
5. Вычисление остатка RX = X − SX − X̃

/* Запуск ESD / обнаружение вектора аномалий XA с X̃ и

MAD при расчете тестовой статистики */

6. XA = ESD(RX, k)
7. v = v + XA

end for

return v

Важно отметить, что длина окон в кусочно-линейном подходе должна быть выбрана таким образом, чтобы окна охватывали как минимум 2 периода любой более крупной сезонности (например, недельной сезонности из-за выходных).

Использование различных аппроксимаций тренда приводит к разным наборам долгосрочных аномалий. Во-первых, сравнивается эффективность предложенного подхода с кусочно-линейной медианой с STL и квантильной регрессией B-сплайном. Во-вторых, сравнивается производительность каждого из них. Наконец, сравнивается, насколько предложенный метод соответствует истинным данным (с помощью внедрения аномалий).

Оценена эффективность предложенного кусочно-медианного подхода, используя производственные данные. В отсутствие классификационных меток, то есть определения того, является ли точка данных аномальной или нет, использовалась информация от группы эксплуатации для оценки ложно-положительных и ложно-отрицательных результатов. На рисунке 3 показано, как STL, квантильная регрессия B-cплайн и кусочно-медианный подходы в контексте выявления аномалий в квартальных данных. Сплошные синие линии показывают основную тенденцию, полученную с помощью каждого подхода.

Рис. 3. Аномалии, обнаруженные с помощью STL (вверху), квантильного B-сплайна (в середине) и кусочно-линейной медианы (внизу)

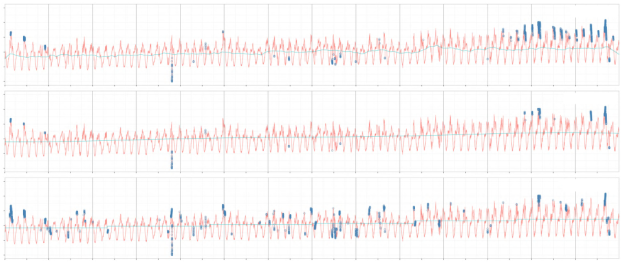
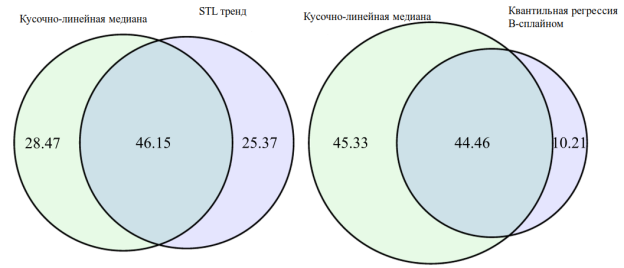
Из рисунка 3 видно, что все три метода способны выявлять наиболее явные аномалии, однако замечено, что общие наборы аномалий, выявляемые этими тремя методами, сильно отличаются. При уточнении результатов со службами эксплуатации выяснено, что STL и квантильная регрессия B-сплайном дают много ложных срабатываний. Квантильная регрессия B-сплайном, по-видимому, более консервативна, но пропускает аномалии во внутри-дневных провалах. Для сравнения, STL обнаруживает некоторые из этих внутри-дневных аномалий, но становится слишком агрессивной к концу временного ряда, выдавая множество ложных срабатываний. В отличие от него, кусочно-линейная медиана обнаруживает большинство внутри-дневных аномалий и имеет гораздо более низкий процент ложных срабатываний, чем STL. Эти выводы также подтверждаются рисунком 4, на котором мы видим, что примерно 45 % аномалий, обнаруженных кусочно-линейной медианой, совпадают с аномалиями, обнаруженными STL и B-сплайном, причём B-сплайн является более консервативным.

Рис. 4. Пересечение и разность множеств аномалий, найденных в STL и квантильном B-сплайне, по сравнению с кусочно-линейной медианой

В реальных данных было замечно, что может быть несколько сезонных компонент, например, ежедневных и еженедельных (например, изменение нагрузки в выходные дни). В связи с этим метод кусочно-линейной медианы предполагает, что каждое окно охватывает по крайней мере один период каждого сезонного шаблона. Это показано на рисунке 5, где представлены пересечения и различия между набором аномалий, полученных с помощью метода кусочно-линейной медианы с использованием того же набора данных, но со «сдвигом фазы» для получения частичных (набор A) и полных (набор B) периодов выходных. Из рисунка видно, что аномалии, обнаруженные с помощью набора A, содержат все аномалии, обнаруженные с помощью набора B; однако в первом наборе было много ложных срабатываний из-за того, что он содержал только частичный период выходных.

Рис. 5. Пересечение и разница между аномалиями, обнаруженными с помощью двухнедельных скользящих окон, содержащих частичные периоды выходных (A) и полные периоды выходных (B)

Обнаружение аномалий в режиме реального времени является ключом к скорости реакции на возникновение нештатных ситуаций. С этой целью была оценена производительность трех методов по скорости выполнения. Анализ производственных данных за три месяца с использованием кусочной медианы занял примерно четыре минуты, в то время как анализ STL и квантильного B-сплайна занял более тринадцати минут. В таблице 1 приведены факторы замедления. Из таблицы мы видим разницу в скорости более чем в 3 раза, что становится недопустимым при анализе данных на годовых интервалах.

Таблица 1

	Среднее значение, мин.	Замедление, раз	Процент аномалий
STL тренд	13,48	3,19	8,6 %
Квантильный B-сплайн	13,62	3,22	5,7 %
Кусочно-медианная	4,23	1	9,5 %

Учитывая скорость, объём и характер данных облачной инфраструктуры в режиме реального времени, нецелесообразно получать данные временных рядов с «истинными» аномалиями. Следовательно, для оценки эффективности предлагаемого метода в контролируемых условиях использовался подход, основанный на внедрении аномалий. Сначала сглаживались производственные данные с помощью разложения временных рядов, в результате чего получилась отфильтрованная аппроксимация временных рядов. Затем случайным образом внедрялись аномалии по двум параметрам — время внедрения и величина аномалии. Каждый набор введенных данных использовался для создания девяти различных тестовых наборов (временных рядов), в 30, 40 и 50 % дней которых во временном ряду была введена аномалия на уровне 1.5, 3 и 4.5σ (стандартное отклонение). Значение 1σ было получено на основе сглаженных данных временного ряда.

Таблица 2

	Среднее значение, мин.	Замедление, раз
STL тренд	21,59	4,49
Квантильный B-сплайн	21,48	4,78
Кусочно-медианная	4,19	1

Как и в случае с реальными производственными данными, STL и квантильный B-сплайн работают медленнее в 4 раза (см. таблицу 2). Более быстрое вычисление кусочно-линейной медианы позволяет анализировать более длинные временные ряды за более короткий период. Это полезно там, где обнаружение аномалий в исторических производственных данных может дать представление о проблеме, требующей решения в кратчайшие сроки.

Рис. 6. Точность, отзывчивость, F-мера

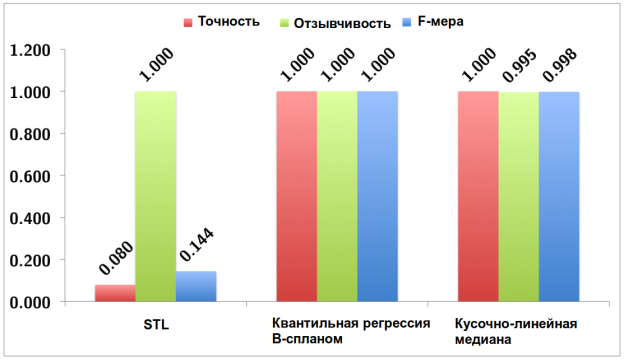
Кроме того, из рисунка 6 видно, что кусочно-линейная медианна работает почти так же хорошо, как квантильный B-сплайн, в то время как STL имеет очень низкую точность. Из представленных результатов видно, что кусочно-линейная медианна является надёжным способом (имеет высокую F-меру) для обнаружения аномалий в долгосрочных облачных данных. Кроме того, кусочно-медианный анализ выполняется в 4 раза быстрее!

Предложен подход, основанный на ESD, для выявления аномалий в данных долгосрочных временных рядов. Для его реализации требуется выявление компонента тренда. Представлены три различных метода для выявления тренда. С использованием реальных данных, рассчитана точность, отзывчивость и F-мера, а также продемонстрирована эффективность использования кусочно-медианного подхода по сравнению с STL и квантильной регрессией B-сплайном. Кроме того, получено значительное ускорение работы алгоритма для кусочно-медианного подхода. В обоих случаях (эффективность и производительность) обнаружение аномалий с помощью кусочно-медианного подхода к выявлению тренда работает так же хорошо, как STL и квантильная регрессия B- сплайном. В настоящее время этот метод планируется использовать в производстве. В качестве дальнейшей работы планируется использовать предложенный подход для смягчения влияния сдвигов среднего значения во временных рядах на обнаружение аномалий.

Литература:

1. Anomaly detection: A Survey. Department of Computer Science and Engineering University of Minnesota.— 2009. — 73 с.

2. Anomaly Detection of Time Series. Facility Of The Graduate School Of The University Of Minnesota. Deepthi Cheboli. — 2010. — 75 c.

3. C Leveland, R. B., C Leveland, W. S., M C Rae, J. E., and T Erpenning, I. STL: a seasonal-trend decomposition procedure based on loess. Journal of Official Statistics 6, 1–1990, — 373 c.

4. Нечеткое моделирование временных рядов и анализ нечетких тенденций. Афанасьева Т. В., Ярушкина Н. Г. — Ульяновск: УлГТУ, 2009. — 299 с