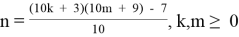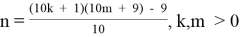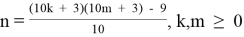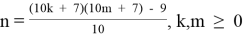Настоящая статья посвящена выводу формул и разработке алгоритма поиска простых чисел в заданном числовом интервале. Данный алгоритм также применим для проверки факта, является ли данное число простым или нет.
Ключевые слова: простые числа, численные методы, алгоритм.
This article is devoted to the derivation of formulas and the development of an algorithm for the search of primes in a given numerical interval. This algorithm is also useful for checking whether a given number is prime or not.
Keywords: primes, numerical methods, algorithm.
Формула простого числа
Натуральное число X в десятичном представлении может оканчиваться на цифры: 1, 3, 7, 9. Очевидно, что число X является простым, если выполняются следующие условия:
X = 10n + 1(1)
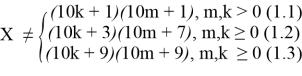
или X = 10n + 3(2)
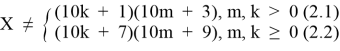
или X = 10n + 7(3)
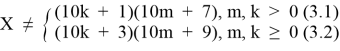
или X = 10n + 9(4)
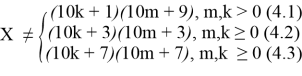
Выбор m и k для описания простого числа
1) Рассмотрим построение простого числа из формулы (1)
1.1. Из формулы (1.1) выразим:
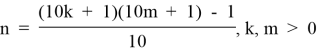
и построим матрицу чисел n, зависящих от m и k. Обозначим ее через T1.1.
1.2. Из формулы (1.2) выразим:
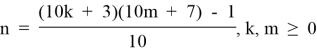
и построим матрицу чисел n, зависящих от m и k. Обозначим ее через T1.2.
1.3. Из формулы (1.3) выразим:
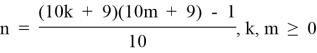
и построим матрицу чисел n, зависящих от m и k. Обозначим ее через T1.3.
Итак, число X = 10n + 1 является простым, если n не равно ни одному из чисел матриц T1.1, T1.2, T1.3, за исключением чисел строки k = 0 матрицы T1.1.
В этой строке все числа имеют вид n = ((10m + 1) — 1) / 10, или n = m, т. е. получается, что в этой строке число X = 10n + 1 равно произведению двух сомножителей — единицы и самого себя, что допустимо для простого числа. Все остальные элементы матрицы T1.1 имеют не менее двух делителей, а это означает, что число (1) будет составным.
2) Рассмотрим построение простого числа из формулы (2)
2.1. Из формулы (2.1) выразим:
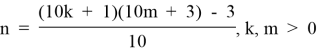
и построим матрицу чисел n, зависящих от m и k. Обозначим ее через T2.1.
2.2. Из формулы (2.2) выразим:
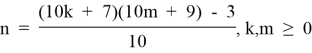
и построим матрицу чисел n, зависящих от m и k. Обозначим ее через T2.2.
Итак, число X = 10n + 3 является простым, если n не равно ни одному из чисел матриц T2.1, T2.2, за исключением строки k = 0 матрицы T.2.1.
3) Рассмотрим построение простого числа из формулы (3)
3.1. Из формулы (3.1) выразим:
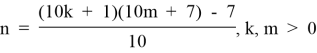
и построим матрицу чисел n, зависящих от m и k. Обозначим ее через T3.1.
3.2. Из формулы (3.2) выразим:
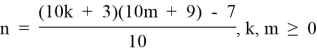
и построим матрицу чисел n, зависящих от m и k. Обозначим ее через T3.2.
Итак, число X = 10n + 7 является простым, если n не равно ни одному из чисел матриц T3.1, T3.2, за исключением строки k = 0 матрицы T.3.1.
4) Рассмотрим построение простого числа из формулы (4)
4.1. Из формулы (4.1) выразим:
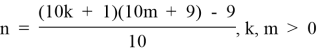
и построим матрицу чисел n, зависящих от m и k. Обозначим ее через T4.1.
4.2. Из формулы (4.2) выразим:
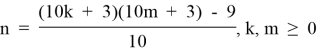
и построим матрицу чисел n, зависящих от m и k. Обозначим ее через T4.2.
4.3. Из формулы (4.3) выразим:
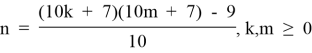
и построим матрицу чисел n, зависящих от m и k. Обозначим ее через T4.3.
Итак, число X = 10n + 9 является простым, если n не равно ни одному из чисел матриц T4.1, T4.2, T4.3, за исключением строки k = 0 матрицы T4.1.
Фрагменты матриц приведены в Приложении. Эти матрицы назовем по имени их разработчика «таблицами Травникова».
Методика нахождения простого числа в заданном интервале
В данном разделе рассмотрим получение простого числа, а также всех простых чисел в заданном интервале.
Мы будем рассматривать поиск простого числа, большего 20. Поиск простого числа, меньшего 20, тривиален и может быть произведен вручную.
Проверка того, является ли данное число простым, это отдельная задача, которую мы рассмотрим в разделе «Проверка числа на простоту».
1. Обозначим интервал поиска простого числа через:
interval_beg — начальное число интервала, interval_end — конечное число интервала, причем, interval_beg и interval_end — натуральные числа и interval_beg ≤ interval_end.
2. Для поиска простого числа необходимо определить число n, которое не будет содержаться ни в одной таблице Травникова. То есть:
— Число n из формулы (1) не должно содержаться в таблицах T1.1, T1.2 и T1.3. Если такое число n будет найдено, то алгоритм возвращает простое число X = 10n + 1 и заканчивает работу.
— Число n из формулы (2) не должно содержаться в таблицах T2.1 и T2.2. Если такое число n будет найдено, то алгоритм возвращает простое число X = 10n + 3 и заканчивает работу.
— Число n из формулы (3) не должно содержаться в таблицах T3.1 и T3.2. Если такое число n будет найдено, то алгоритм возвращает простое число X = 10n + 7 и заканчивает работу.
— Число n из формулы (4) не должно содержаться в таблицах T4.1, T4.2 и T4.3. Если такое число n будет найдено, то алгоритм возвращает простое число X = 10n + 9 и заканчивает работу.
3. Поиск в соответствующей таблице будем производить только среди тех чисел n, которые удовлетворяют условию:
n_beg ≤ n ≤ n_end, где n_beg = interval_beg / 10, а n_end = interval_end / 10.
4. На начальном шаге n = n_beg. Будем искать поочередно числа вида (1), (2), (3), (4). Если число n будет совпадать с одним из чисел из соответствующих таблиц Травникова, а это означает, что число X составное, то увеличим число n = n + 1 и далее опять произведем поиск и т. д. и так до тех пор, пока n не станет равным n_end.
5. Если не будет найдено ни одно число n, которое не будет содержаться в соответствующей таблице Травникова, то это будет означать, что в данном интервале простых чисел не существует. В этом случае надо расширить интервал поиска и повторить поиск.
6. Для поиска среди элементов таблиц Травникова необходимо найти номера строк, а в каждой строке номера столбцов, среди которых будет происходить поиск. Номер строки k должен удовлетворять условию: k_beg ≤ k ≤ k_end, номер столбца m должен удовлетворять условию: m_beg ≤ m ≤ m_end, где k_beg и m_beg соответствуют n_beg, а k_end и m_end соответствуют n_end.
Алгоритм нахождения номеров строк и столбцов
Алгоритм поиска простого числа вида X = 10n + 1 рассмотрим более подробно. В остальных случаях рассуждения аналогичны и мы просто приведем формулы.
Округление вниз и вверх производится для того чтобы не сузить диапазон поиска.
Таблица T1.1
— k_beg = 1. Строка с k = 0 исключается из поиска.
— Так как таблица T1.1. является симметричной относительно главной диагонали, будем производить поиск только в правой ее части, т. е. когда m ≥ k.
На диагонали выполняется условие: n_diag = (X-1) / 10 = 10k 2 + 2k. Мы ищем номер строки, для которой будет выполняться условие:
n_end ≤ n_diag. Для этого решим квадратное уравнение:
10k 2 + 2k — n_end = 0. Отсюда находим:
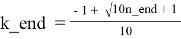
— Далее в каждой из строк таблицы T1.1 будем искать номера столбцов, удовлетворяющих условию: m_beg ≤ m ≤ m_end, и только среди этих столбцов будет происходить поиск.
Подставим n_beg в формулу X = 10n + 1 = (10k + 1)(10m + 1) и выразим m_beg в зависимости от k.
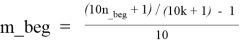
Затем ищем максимум для того, чтобы работать только в правой части таблицы, т. е. m_beg = Max{m_beg, k}.
— Подставим n_end в формулу X = 10n + 1 = (10k + 1)(10m + 1) и выразим m_end в зависимости от k.
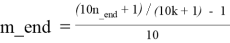
Таблица T 1.2
— k_beg = 0.
— из формулы (1.2) получим:
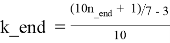
Для каждого k_beg ≤ k ≤ k_end в каждой строке таблицы T1.2 справедливы следующие формулы:
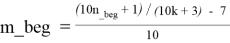
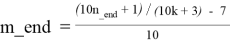
Таблица T1.3
— k_beg = 0.
— Так как таблица T1.3. является симметричной относительно главной диагонали, будем производить поиск только в правой ее части, то есть когда m ≥ k.
На диагонали выполняется условие:
n_diag = (X-1) / 10 = 10k 2 + 18k + 8. Мы ищем номер строки, для которой будет выполняться условие: n_end ≤ n_diag. Для этого решим квадратное уравнение: 10k 2 + 18k + 8 — n_end = 0. Отсюда находим:
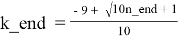
Для каждого k_beg ≤ k ≤ k_end в каждой строке таблицы T1.3 справедливы следующие формулы:
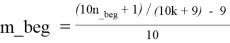
m_beg = Max{m_beg, k}
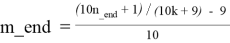
Таблица T 2.1
— k_beg = 1. Строка с k = 0 исключается из поиска.
— из формулы (2.1) получим:
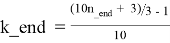
Для каждого k_beg ≤ k ≤ k_end в каждой строке таблицы T2.1 справедливы следующие формулы:
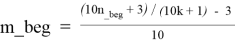
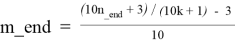
Таблица T2.2
— k_beg = 0.
— из формулы (2.2) получим:
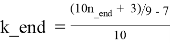
Для каждого k_beg ≤ k ≤ k_end в каждой строке таблицы T2.2 справедливы следующие формулы:

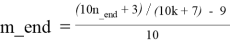
Таблица T3.1
— k_beg = 1. Строка с k = 0 исключается из поиска.
— из формулы (3.1) получим:
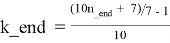
Для каждого k_beg ≤ k ≤ k_end в каждой строке таблицы T3.1 справедливы следующие формулы:
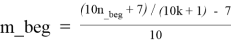
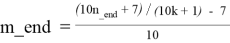
Таблица T 3.2
— k_beg = 0.
— из формулы (3.2) получим:
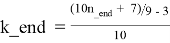
Для каждого k_beg ≤ k ≤ k_end в каждой строке таблицы T3.2 справедливы следующие формулы:
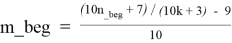
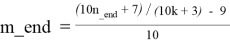
Таблица T4.1
— k_beg = 1. Строка с k = 0 исключается из поиска.
— из формулы (4.1) получим:
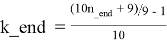
Для каждого k_beg ≤ k ≤ k_end в каждой строке таблицы T4.1 справедливы следующие формулы:

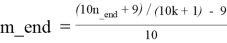
Таблица T4.2
— k_beg = 0.
— из формулы (4.2) получим:
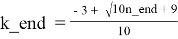
Для каждого k_beg ≤ k ≤ k_end в каждой строке таблицы T4.2 справедливы следующие формулы:
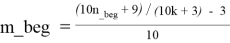
m_beg = Max{m_beg, k}.
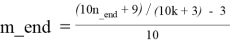
Таблица T 4.3
— k_beg = 0.
— из формулы (4.3) получим:
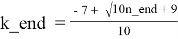
Для каждого k_beg ≤ k ≤ k_end в каждой строке таблицы T4.3 справедливы следующие формулы:
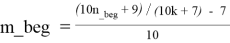
m_beg = Max{m_beg, k}.
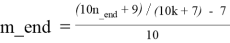
Пример поиска первого простого числа в интервале
Покажем, как найти первое простое число вида (1) в интервале от 120 до 150. Поиск необходимо проводить не во всех клетках таблиц, а только в затененных.
— Положим n = 12. Это число содержится в таблице T1.1, следовательно, это число составное.
— n = n + 1, т. е. n = 13. Число n не содержится ни в одной из затененных клеток таблиц T1.1 — T1.3, следовательно, число X = 10 . n + 1 = 10 . 13 + 1 = 131 является простым.
— Алгоритм заканчивает свою работу. В Приложении приведены фрагменты таблиц T1.1 — T1.3 с затененными клетками.
Методика нахождения всех простых чисел в заданном интервале
— Положим n = n_beg. Будем искать поочередно числа вида (1), (2), (3), (4).
— Применяем алгоритм нахождения простого числа. Если не будет найдено ни одного простого числа, алгоритм заканчивает свою работу.
— Если простое число будет найдено, увеличим число n = n + 1 и т. д. до тех пор, пока n не станет равным n_end.
Проверка числа на простоту
Рассмотрим алгоритм проверки числа на простоту. Применим тот же алгоритм, что и для поиска простых чисел в заданном интервале. Положим X = interval_beg = interval_end, где X — число, требующее проверки на простоту. В таблице, приведенной ниже, собраны данные проверки различных чисел на простоту.
Таблица 1
Проверка чисел на простоту
|
Число — простое или нет |
Количество операций (метод Князевой-Травникова) |
Количество операций (классический метод) |
|
101 — да |
27 |
99 |
|
143 — нет |
10 |
10 |
|
1 001 — нет |
6 |
6 |
|
1 303 — да |
135 |
1301 |
|
1 779 — нет |
2 |
2 |
|
10 007 — да |
527 |
10 005 |
|
110 143 — нет |
10 |
10 |
|
7791331 — нет |
16 642 |
46 |
|
10 111 111 — нет |
48 |
28 |
|
10 951 373 — да |
973 475 |
10 951 371 |
|
37 245 489 — нет |
2 |
2 |
|
37 245 473 — да |
3 310 727 |
37 245 471 |
|
100 140 049 — нет |
2 229 357 |
10 006 |
|
109 479 871 — да |
3 132 200 |
109 479 869 |
|
267 323 443 — нет |
17 821 607 |
126 |
|
267 323 461 — да |
7 644 373 |
267 323 459 |
|
1 111 111 117 — нет |
9056 |
22 |
|
1 131 141 157 — да |
57 454 809 |
1 131 141 155 |
|
51 545 202 857 — да |
2 618 169 053 |
51 545 202 855 |
|
372 715 448 311 — нет |
7 571 214 |
10 006 |
Проанализировав данные таблицы, мы можем сделать следующие выводы:
- Если число является составным, то количество операций классическим методом в среднем равно 9.9 % от количества операций методом Князевой-Травникова.
- Если число является простым, то количество операций методом Князевой-Травникова составляет в среднем 8,5 % от количества операций классическим методом.
- Выбор метода для проверки числа на простоту остается за пользователем.
Приложение.
Таблицы Травникова
Таблица 2
Фрагмент таблицы T1.1,
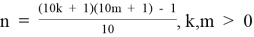
|
m k |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
... |
|
0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
... |
|
1 |
12 |
23 |
34 |
45 |
56 |
67 |
78 |
89 |
100 |
... | |
|
2 |
44 |
65 |
86 |
107 |
128 |
149 |
170 |
191 |
... | ||
|
3 |
96 |
127 |
158 |
189 |
220 |
251 |
282 |
... | |||
|
4 |
168 |
209 |
250 |
291 |
332 |
373 |
... | ||||
|
5 |
260 |
311 |
362 |
413 |
464 |
... | |||||
|
6 |
372 |
433 |
494 |
555 |
... | ||||||
|
7 |
504 |
575 |
646 |
... | |||||||
|
8 |
656 |
737 |
... | ||||||||
|
9 |
828 |
... | |||||||||
|
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
Таблица является симметричной.
Таблица 3
Фрагмент таблицы T1.2,
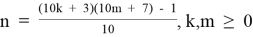
|
Таблица 4
Фрагмент таблицы T1.3,
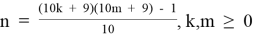
|
Таблица является симметричной.
Таблица 5
Фрагмент таблицы T2.1,
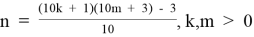
|
Таблица 6
Фрагмент таблицы T2.2,
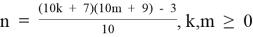
|
Таблица 7
Фрагмент таблицы T3.1,
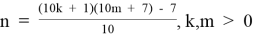
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Таблица 8
Фрагмент таблицы T3.2,
Таблица 9
Фрагмент таблицы T4.1,
Таблица 10
Фрагмент таблицы T4.2,
Таблица является симметричной. Таблица 11
Фрагмент матрицы T4.3,
Таблица является симметричной. Таблица 12 Фрагмент таблицы T1.1 с затененными клетками
Таблица 13 Фрагмент таблицы T1.2 с затененными клетками
Таблица 14 Фрагмент таблицы T1.3 с затененными клетками
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||