Вданной статье рассмотрено решение проблемы уменьшения суммы квадратов отклонений определённых функций от искомых переменных для полиномиальных уравнений n степени. Приведено подробное решение для уравнений 2 степени, рассматриваемой проблемы. Представлена рабочая программа.

Ключевые слова: метод наименьших квадратов, полиномы, полиномиальная регрессия, оконное приложение.

Метод наименьших квадратов — один из методов статистики, имеющий различное практическое применение, в основе которого лежит минимизация суммы квадратов отклонений функций от подлежащих нахождению переменных [4].

История создания.

Одной из основных задач, для решения которой применяется метод наименьших квадратов, является решение систем линейных уравнений, в которых число неизвестных переменных меньше, чем число уравнений. Впервые, метод был применён в 1796 году Фридрихом Гауссом, а в 1805 году Адриен Лежандр опубликовал метод под насущным названием. Метод в дальнейшем был доработан и улучшен [4].

Суть метода.

Допустим, что x — группа nнеизвестных переменных: –набор функций от группы переменных. Целью является подбор таких x, чтобы значения функций были близки к yi [3]. Следовательно, суть метода наименьших квадратов может быть выражена следующей формулой:

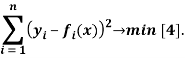
Полиномиальная регрессия.

Допустим, что имеется nзначений переменной yи соответствующих переменных x. Необходимо аппроксимировать корреляцию между yи xопределённой функцией f(x,a), где a–известные параметры.

В случае, когда имеется некоторая полиномиальная регрессионная зависимость, например: 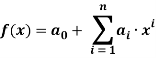можно определить параметры системы, учитывая, что а также

Тогда, матричные уравнения будут иметь следующий вид:

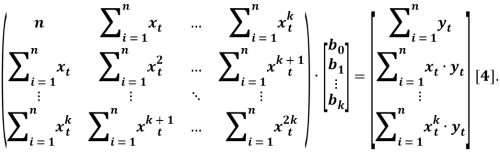
Цель работы.

Целью проводимой работы является вывод рабочих формул, минимизирующих сумму квадратов отклонений полиномиальной функции 2 степени, а также создание практической программы, позволяющей находить коэффициенты квадратичной функции и полинома nстепени. Приложение будет являться оконным (будет предусмотрена возможность построения графика по заданным точкам).

Математическое решение проблемы для полиномов 2 степени.

Пусть дан полином второй степени вида:

Пусть задана функция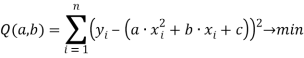

Тогда: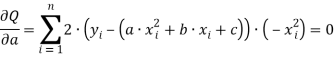 (двойку можно сократить)

В итоге имеем: 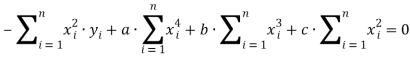(Преобразуем к виду (1) см. ниже)

Тогда: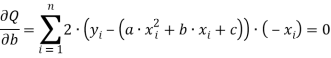 (двойку можно сократить)

В итоге имеем: 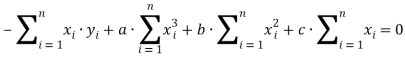(Преобразуем к виду (2) см. ниже)

Тогда: 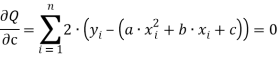(двойку можно сократить)

В итоге имеем: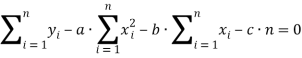 (Преобразуемк виду (3) см. ниже)

Составим систему линейных уравнений:

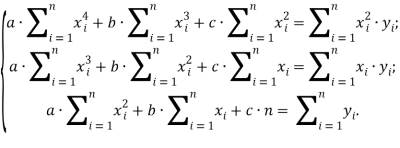
Решим систему. Найдём определитель системы:

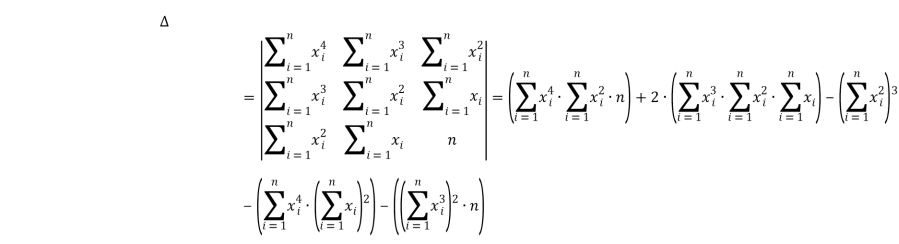
Найдём первый частный определитель системы:

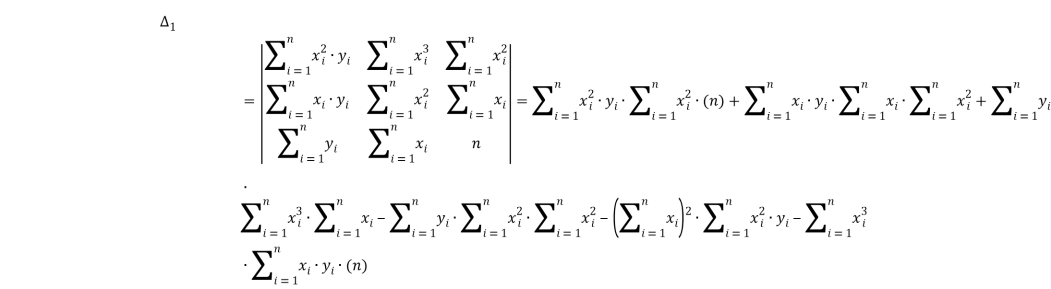
Найдём второй частный определитель системы:

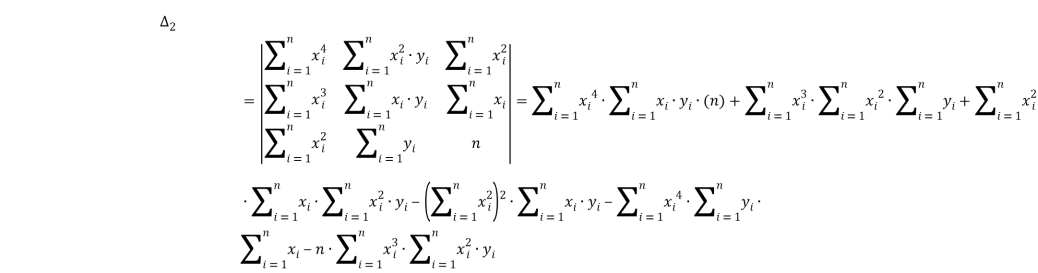
Найдём третий частный определитель системы:

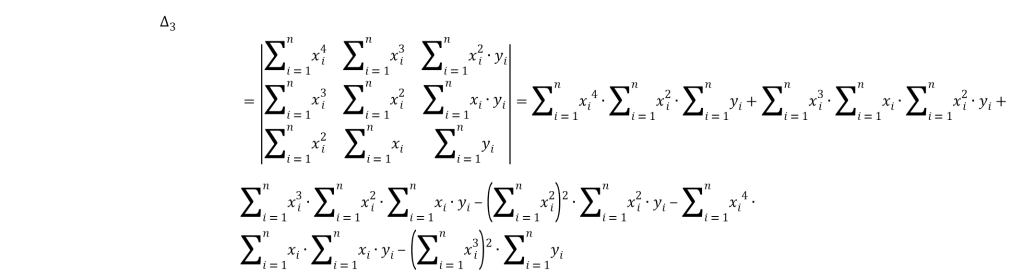
, b=, c=.

Решение проблемы для полиномов n степени.

Пусть дан полином вида: , где , а длина отрезка известных нам значений [2].

Необходимо найти такие параметры , чтобы сумма квадратов отклонений от в точках была минимальной, то есть

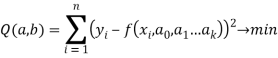
Задача сводится к решению системы уравнений:

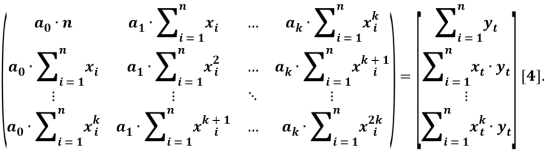
Для решения будем использовать метод Гаусса. Результат решения системы можно наблюдать в работе оконного приложения на языке программирования C#.

Программа

Оконное приложение на языке программирования C# для определения коэффициентов аппроксимации полиномов nстепени.

Основная работа программы приходится на обработчик нажатия кнопки вычислить. Считывается степень полинома. Вычисляется кол-во точек. Далее по заданным точкам заполняется матрица сумм. Далее матрица сумм приводится к такому виду, чтобы на главной диагонали не было нулей. Высчитываются коэффициенты аппроксимации.

Программа позволяет импортировать данные из текстового файла, строить график получившейся функции и сохранять его в формате.png, экспортировать в текстовый файл получившиеся коэффициенты.

Оконные формы приложения:

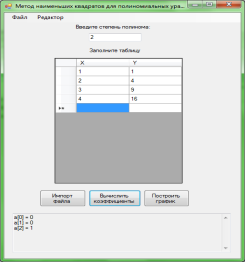
Рис. 1. Оконное приложение, реализующее метод наименьших квадратов для полиномиальных уравнений n степени.

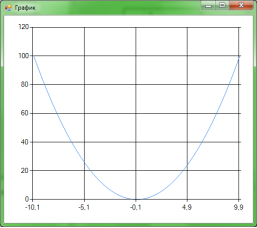
Рис. 2. Полученный график, аппроксимированной функции.

Программа доступна к использованию по ссылке: https://yadi.sk/d/G9WiaoGe3UYqsJ

Вывод

В ходе работы были выведены рабочие формулы, минимизирующие сумму квадратов отклонений полиномиальной функции второй и n-ой степени, а также была создана практическая программа, позволяющая находить коэффициенты аппроксимируемой функции.

Разработанная программа может применяться при расчётах в эконометрике для наглядного определения зависимостей одних зависимостей от других, также в оценке параметров однофакторной эконометрической модели и других областях науки.

Литература:

1. Письменный Т.Д — Конспект лекций по высшей математике
2. NetBeansURL: https://netbeans.org/ (Дата обращения: 5.4.18).
3. Аппроксимация функций полиномом методом наименьших квадратов.URL: http://www.alexeypetrov.narod.ru/C/sqr_less_about.html (Дата обращения: 6.4.18)
4. Материал из Википедии — свободной энциклопедии. Метод наименьших квадратов. URL: https://ru.wikipedia.org/wiki/Метод_наименьших_квадратов (Дата обращения: 6.4.18).