В данной статье рассматривается задача линейного программирования и возможный способ её решения — симплекс метод. Приведены примеры, поясняющие, что такое линейное программирование и симплекс метод.
Ключевые слова: линейное программирование, математическая оптимизация, pivot-переменная, симплекс метод, slack variables
Линейное программирование — это мощный инструмент для описания и решения задач оптимизации. Возьмем простой пример и рассмотрим задачу минимизации стоимости продуктов, соответствующих ежедневным нормам рациона человека. Модель линейного программирования имела бы множество переменных решений, которые подразумевают под собой количество каждого покупаемого продукта. Цель данной задачи — минимизировать стоимость приобретения выбранных продуктов, имея ограничения в виде питательных веществ.
Используя алгебраическую нотацию, линейное программирование может быть описано следующим образом:
Objective: minimize cTx
Constraints: Ax = b (ограничения линейного вида) / l ≤ x ≤ u (ограничения на заданном интервале).
В результате описания в данной форме, вектор х представляет собой вектор переменных решений, с — линейная целевая функция, матричное уравнение Ах = b указывает линейные ограничения в х, векторы l и u — нижнюю и верхнюю границы в х.
Пример нахождения минимального и максимального значения:
Допустим вам необходимо купить шкафы для хранения документов. Известно, что 10 единиц стоит шкаф Х, который хранит 8 м2 файлов и требует пространства 6 м2. С другой стороны, известно, что 20 единиц стоит шкаф У, который хранит 12 м2 и требует 8 м2. Имеется 140 единиц денег, а также помещение размером 72 м2.
Подставляем значения в решение:
Количество хранимого:
![]()
Пространство:
![]()
Стоимость:
![]()
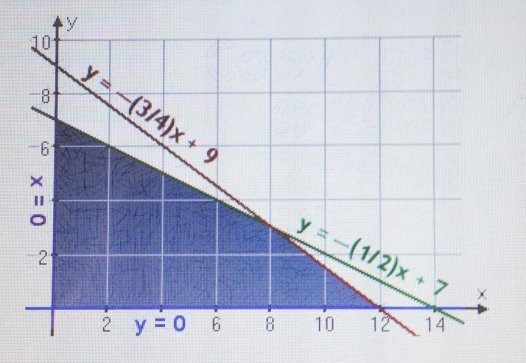
Рис. 1. Графическое представление задачи
Из графика видно, что решение соответствует точкам (8, 3).
Первый алгоритм для решения задач линейного программирования был создан американским математиком Джорджом Данцигом в 1947 году.
Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве.
Сущность метода: построение базисных решений, на которых монотонно убывает линейный функционал, до ситуации, когда выполняются необходимые условия локальной оптимальности.
История линейного программирования
В работе Л. В. Канторовича «Математические методы организации и планирования производства» (1939) были впервые изложены принципы новой отрасли математики, которая позднее получила название линейного программирования.
Исторически общая задача линейного программирования была впервые поставлена в 1947 году Джорджом Бернардом Данцигом, Маршаллом Вудом и их сотрудниками в департаменте военно-воздушных сил США. В то время эта группа занималась исследованием возможности использования математических и смежных с ними методов для военных задач и проблем планирования. В дальнейшем для развития этих идей в ВВС была организована исследовательская группа под названием «Project SCOOP». Первое успешное решение задачи линейного программирования на ЭВМ SEAC было проведено в январе 1952 года [2].
Эффективность
Симплекс метод удивительно эффективен на практике, но в 1972 Кли и Минти привели пример, в котором симплекс-метод перебирал все вершины симплекса, что показывает экспоненциальную сходимость метода в худшем случае. С тех пор для каждого варианта метода был найден пример, на котором метод вел себя исключительно плохо.
Наблюдения и анализ эффективности метода в практических приложениях привело к развитию других способов измерения эффективности.
Симплекс метод имеет среднюю полиномиальную сходимость при широком выборе распределения значений в случайных матрицах.
Вычислительная эффективность оценивается обычно при помощи двух параметров:
- Числа итераций, необходимого для получения решения;
- Затрат машинного времени.
В результате численных экспериментов получены результаты:
- Число итераций при решении задач линейного программирования в стандартной форме с M ограничениями и N переменными заключено между M и 3M. Среднее число итераций 2M. Верхняя граница числа итераций равна 2M+N.
- Требуемое машинное время пропорционально M3.
Число ограничений больше влияет на вычислительную эффективность, чем число переменных, поэтому при формулировке задач линейного программирования нужно стремиться к уменьшению числа ограничений пусть даже путём роста числа переменных.
Покажем суть метода на примере:
Владельцу предприятия, производящего трейлеры, необходимо определить лучший набор 3 продуктов: трейлер с прицепом, экономичный трейлер или трейлер высокого качества. Предприятие ограничено работой 24 днями на металлообработке и 60 днями на деревообработке для разработки трейлеров. Следующая таблица наглядно представит задачу:
|
С прицепом |
Экономичный |
Высокого качества |
Ограничения (дней) | |
|
Металлообработка |
0.5 |
2 |
1 |
24 |
|
Деревообработка |
1 |
2 |
4 |
60 |
|
Выручка за единицу |
6 |
14 |
13 |
Обозначим трейлеры за х1, х2, х3.
Необходимо:
![]()
Согласно ограничениям:
0.5x1+2x2+x3 ≤24
x1+2x2+4x3 ≤60
![]()
Неравенства «≥» и «≤» необходимо привести к равенствам с помощью добавления переменных, в английской литературе называемых slack variables.
0.5x1+2x2+x3+x4=24
x1+2x2+4x3+x5=60
Далее необходимо выбрать pivot переменную:
|
BASIS |
X1 |
X2 |
X3 |
X4 |
X5 |
Ограничения |
Отношение |
Pivot |
|
X4 |
0.5 |
2 |
1 |
1 |
0 |
24 |
12 |
* |
|
X5 |
1 |
2 |
4 |
0 |
1 |
60 |
30 | |
|
-z |
-6 |
-14 |
-13 |
0 |
0 |
0 | ||
|
Pivot |
* |
Выбранный алгоритмом элемент выделен жирным. Далее необходимо “занулить” столбец с pivot переменной, а также привести её к 1. В столбце basis Х4 заменяется на Х2, так как pivot в столбце Х2 и строке Х4.
Результат:
|
BASIS |
X1 |
X2 |
X3 |
X4 |
X5 |
Ограничения |
Отношение |
Pivot |
|
X2 |
0.25 |
1 |
0.5 |
0.5 |
0 |
12 |
24 | |
|
X5 |
0.5 |
0 |
3 |
-1 |
1 |
36 |
12 |
* |
|
-z |
-2.5 |
0 |
-6 |
7 |
0 |
168 | ||
|
Pivot |
* |
Операция повторяется:
|
BASIS |
X1 |
X2 |
X3 |
X4 |
X5 |
Ограничения |
Отношение |
Pivot |
|
X2 |
1/6 |
1 |
0 |
2/3 |
-1/6 |
6 |
36 |
* |
|
X3 |
1/6 |
0 |
1 |
-1/3 |
1/3 |
12 |
72 | |
|
-z |
-1.5 |
0 |
0 |
5 |
2 |
240 | ||
|
Pivot |
* |
Операция повторяется:
|
BASIS |
X1 |
X2 |
X3 |
X4 |
X5 |
Ограничения |
Отношение |
|
X1 |
1 |
6 |
0 |
4 |
-1 |
36 |
36 |
|
X3 |
0 |
-1 |
1 |
-1 |
0.5 |
6 |
6 |
|
-z |
0 |
9 |
0 |
11 |
0.5 |
294 |
Таким образом, решение минимума z = -294. Максимум равен 294. Оптимальное решение х = (36, 0, 6, 0, 0).
В результате решения задач становится понятно, что симплекс метод является чрезвычайно полезным инструментом в области линейного программирования, несмотря на его простоту.
Литература:
- Singiresu S. Rao Engineering optimization: theory and practice. — New York: Wiley, 2009. — 813 p.
- Гасс С. Линейное программирование. — М.: Государственное издательство физико-математической литературы, 2015. — 304 c.

