В данной статье рассматривается китайская теорема об остатках и ее следствия. Особое внимание уделяется задаче о построении изоморфизма в кольце многочленов и некоторым задачам теории делимости в кольце целых чисел.
Ключевые слова: китайская теорема об остатках, система сравнений, алгоритм Гарнера, кольцо многочленов, кольцо целых чисел, изоморфизм колец
This article discusses the Chinese remainder theorem and its consequences. Particular attention is paid to the problem of constructing an isomorphism of the ring of polynomials and some problems of the theory of divisibility in the ring of integers.
Keywords: Chinese Remainder Theorem, the system comparisons, Garner algorithm, polynomial ring, ring of integers, the ring isomorphism
В фундаментальной математике китайская теорема об остатках применяется для упрощения выражений, при доказательстве тождеств, теорем, например в теории чисел [1, с. 51]; для построения изоморфизмов колец и т. д. В дальнейшем будут представлены задачи, касающиеся различных областей главных идеалов, которые решаются или упрощаются при помощи данной теоремы. А также будет построена интерпретация данной теоремы с точки зрения теории колец.
Китайская теорема об остатках в арифметической формулировке впервые была упомянута в трактате китайского математика Сунь Цзы предположительно в третьем веке н. э. [2, c. 36]. Данная теорема помогает свести некоторое сравнение по модулю к системе более простых сравнений, и наоборот, свести систему сравнений к одному сравнению.
Сформулируем теорему для области главных идеалов.
Теорема 1 (китайская теорема об остатках): Рассмотрим область главных идеалов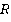 
. Предположим, что 
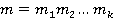и что 
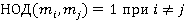. Пусть 
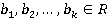, и рассмотрим систему сравнений 
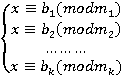. Эта система всегда имеет решение, и любые два решения отличаются на кратное элемента 
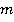[1, с. 50].
Следствие 1:Решение системы сравнений определяется по следующей формуле: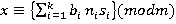 
, 
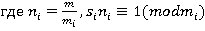[2, c. 36].
Что бы найти обратный элемент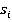 
для элемента 
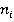, в некоторых случаях удобно использовать следующую теорему:
Теорема 2: Пусть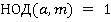 
и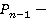 
числитель предпоследней подходящей дроби для числа 
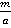. Тогда 
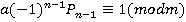, то есть число 
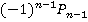является обратным к элементу 
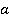по модулю 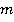[3, c. 405].
Следствие 2: Рассмотрим сравнение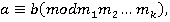 
при этом 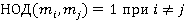. Оно равносильно системе сравнений (
) 
.
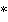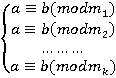Существует также специальный алгоритм для нахождения корня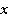 
, названный как алгоритм Гарнера. Суть его в следующем:
Рассмотрим систему сравнений 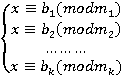. Корень 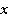можно вычислить как 
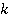— й член последовательности 
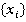. Последовательности , 
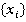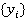строятся по следующим формулам:
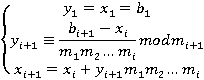
Достоинство этого алгоритма заключается в том, что для вычисления каждой последующей пары (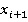
, 
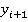) используется только одно предыдущее значение (
, 
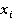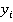), что позволяет последовательно уточнять значения корня 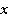[2, с. 37].
Можно также рассматривать не только кольцо целых чисел, но и любые другие области главных идеалов, например, кольцо гауссовых целых чисел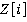 
, кольцо целых чисел Эйзенштейна 
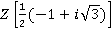, кольцо многочленов 
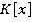над полем 
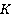, кольцо формальных степенных рядов. Отметим, что для многочленов теорема будет иметь следующий вид:
Теорема 3: Предположим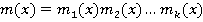, что 
и что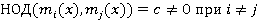 
. Пусть 
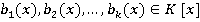, и рассмотрим систему сравнений 
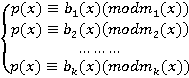. Эта система всегда имеет решение, и любые два решения отличаются на кратное многочлена 
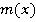, причем 
.
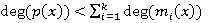Указав основные теоретические аспекты, рассмотрим решения некоторых задач.
Задача 1: Определить все целые числа x, при условии, что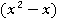 
делится на 
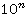, где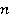 
— натуральное число (к данной задаче относятся также все ребусы типа 
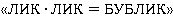, где вместо букв нужно поставить определенные цифры).
Решение: Рассмотрим сравнение в кольце целых чисел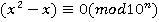 
; Очевидно, что два класса решений оно точно имеет: 
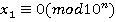и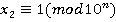 
; Посмотрим, есть ли еще какие либо решения. Применяя китайскую теорему об остатках, получим:
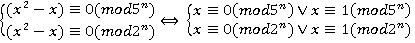. Составляя всевозможные комбинации сравнений по модулям дающих в произведении 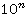, получим следующие системы: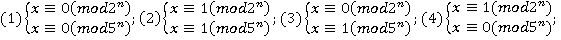 
Решение каждой системы находим, применяя следствия теоремы 1 или алгоритм Гарнера. Применяя следствие 1, получим соответственно для систем (3) и (4):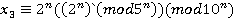 
, 
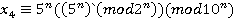, где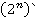 
— обратный элемент к 
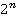по модулю 
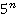, а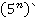 
— обратный элемент к 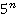по модулю 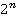. По следствию 2, системе (1) соответствует 
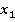, а системе (2) соответствует 
.
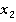Таким образом, все искомые целые числа лежат в классах:
; ; ; 
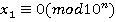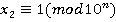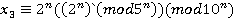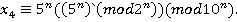
Рассмотрим частный случай общего решения задачи 1. Например, при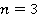 
, получим 
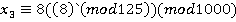, тогда после упрощения получим 
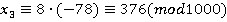. Аналогично 
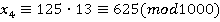. Если рассмотреть ребус 
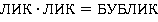, то именно данное частное решение соответствует решению данного ребуса. Действительно, произведем следующие преобразования: 
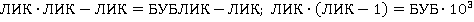, обозначая 
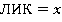, сведем задачу к решению сравнения 
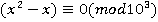. Решение данного сравнения имеет вид: 
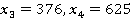, но решением исходной задачи является только 
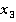. В самом деле, 
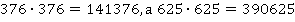(цифры в разряде тысяч и в разряде сотни тысяч должны быть одинаковыми).
Приведем интерпретацию теоремы 1 с точки зрения теории колец. Рассмотрим кольца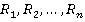 
. Прямая сумма 
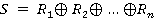данных колец определяется как множество 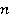— наборов (
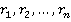) c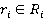 
. Сложения и умножения в кольце 
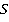определяется следующим образом:
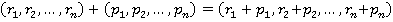
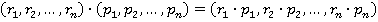
Нулевым элементов будет элемент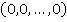 
, единичным элементом — 
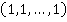. Элемент 
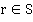, будет обратимым тогда и только тогда, когда существует 
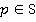, такой, что 
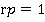. Есл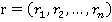и 
и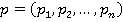 
, то из 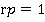следует, что 
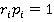при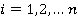 
. Обратно, если 
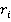— обратимый для каждого 
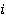, то 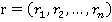— обратимый [1, c. 50]. Таким образом, 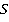кольцо.
Итак, имеет место теорема:
Теорема 4: Пусть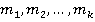 
попарно взаимно простые элементы из кольца 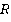. Тогда 
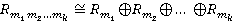, где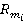 
— факторкольцо кольца 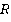по главному идеалу 
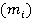[1, c.51].
Если в качестве области главных идеалов взять кольцо целых чисел и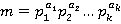 
(это каноническое разложение, где 
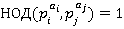), то получим 
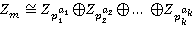, т. е. каждому классу вычетов
факторкольца 
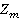соответствует некоторая система классов вычетов прямой суммы факторколец 
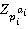. Если 
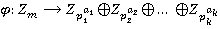данный изоморфизм, то:
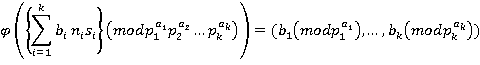
или
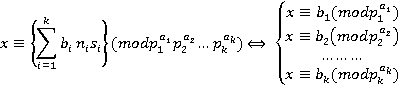
Задачи 2: Рассмотрим классы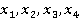 
из решения задачи 1. Доказать, что 
.
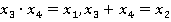Решение: Докажем, применяя теорему 4, например, что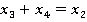 
. По теореме 4: 
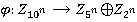— изоморфизм. Тогда из систем (3) и (4), получим: 
; 
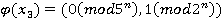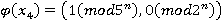. В силу сохранения операции при изоморфизме, правила сложения в кольце 
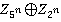и биекции: 
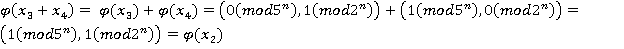. Так как 
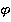— биекция, то существует обратное отображение 
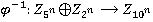, откуда следует что, 
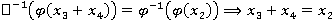. Аналогично доказывается второе соотношение. В итоге:
;
;
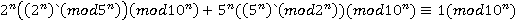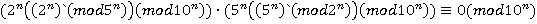Задача 3: Пусть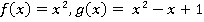 
. Построить изоморфизм колец 
.
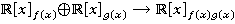Решение: Необходимо для любой пары многочленов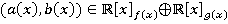 
, найти такой многочлен 
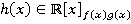, что (по теореме 3):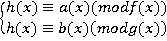 
По следствию 1 решение должно выглядеть следующим образом:
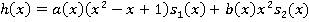. Найдем 
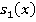и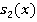 
:
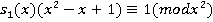. Произведем замену переменной 
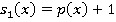, тогда 
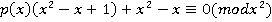. Если взять 
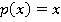, то получим многочлен вида 
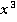, который делиться на 
: 
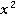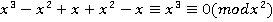. Таким образом, 
.
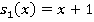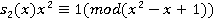. Нетрудно заметить, что 
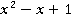есть неполный квадрат суммы кубов. Поэтому 
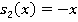. Действительно, 
.
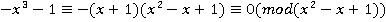Значит, изоморфное отображение 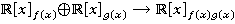задается по следующему правилу: 
.
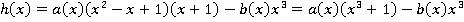Таким образом, на примерах задач 1, 2, 3 показана ценность китайской теоремы об остатках для фундаментальной математики.
Литература:
1. Айерелэнд К., Роузен М. Классическое введение в современную теорию чисел: Пер. с англ. — М.: Мир, 1987. — 416 с.
2. Ишмухаметов Ш. Т. Методы факторизации натуральных чисел: учебное пособие. — Казань: Казан. ун., 2011. — 190 с.
3. Куликов Л. Я. Алгебра и теория чисел: Учебное пособие для педагогических институтов — М.: Высшая школа, 1979. — 559 с.
