Итеративный метод для решения транспортной задачи с дополнительными пунктами производства и потребления и квадратичным штрафом



Ранее [1] был предложен метод решения классической транспортной задачи, основанный на декомпозиции исходной задачи на последовательность двумерных задач с последовательным пересчетом коэффициентов целевых функций. В настоящей работе метод распространяется на случай, когда имеются дополнительные пункты производства и потребления и стоимость перевозки из этих пунктов квадратично зависит от объёмов перевозки. Тем самым, алгоритм напрямую переносится на важный класс нелинейных задач транспортного типа.

Введение. Известные алгоритмы решения транспортных задач основаны на методе улучшения плана в линейном программировании (см., например [1,2]). Транспортная специфика приводит к оригинальным конструкциям симплекс-метода. Однако распространение на более широкие транспортные постановки иногда приводит к большим трудностям, где указанная специфика перестаёт давать прозрачные построения. В данной работе рассматривается транспортная задача с промежуточными пунктами потребления и производства. Формально это приводит к появлению слабых переменных в ограничениях. Даже рассмотрение линейного функционала на этих переменных приводит к серьёзному усложнению алгоритмов на основе метода улучшения плана. Здесь же берутся квадратичные штрафы за перевозку продукта из собственных пунктов потребления и производства. Исходная задача становится нелинейной. Как её решать на основе симплекс-метода — вопрос не простой. Напомним, что стандартная схема симплекс-метода в применении к классической транспортной задаче предполагает запись таблицы, в клетках которой последовательно меняются значения неизвестных количеств перевозок. При этом строятся циклы, где переносятся количества продуктов, что соответствует изменению базисных и внебазисных переменных. Данная интерпретация при дополнительных производствах и потреблениях перестаёт работать. Здесь используется алгоритм, предложенный в [3], основанный на последовательном решении двумерных задач о ранце с лестничной структурой. Основой для этого метода являются подходы для оптимизации сетевых задач [4–6] с промежуточными булевыми переменными с унимодулярными матрицами. Указанный алгоритм напрямую распространяется для рассматриваемого в данной работе класса квадратичных задач транспортного типа с промежуточными пунктами потребления и производства.

1. Постановка задачи. Имеется, как и в классической транспортной задаче m пунктов производства и n пунктов потребления. В каждом ом пункте производства задан объем производства . В каждом ом задан объем потребления . Кроме того, имеются еще n дополнительных пунктов производства. Каждый й дополнительный пункт производства может поставлять свою продукцию только ому пункту потребления. Стоимость перевозки из ого дополнительного пункта производства квадратично зависит от объемов перевозки. Имеется также m дополнительных пунктов потребления. Каждому ому дополнительному пункту потребления продукцию может поставлять только ый обычный пункт производства. Объем потребления в дополнительных пунктах не ограничен. Необходимо минимизировать суммарные затраты на перевозки.

Формальная запись задачи имеет вид:

(1)

(2)

(3)

— целые.(4)

Кроме того, будем считать четными числами, что не ограничивает общности рассмотрения.

2. Метод решения задачи. Первый этап. Сформируем одномерных задач. Первые m одномерных задач имеют вид (‑фиксировано):

(5)

(6)

— целые.(7)

Задача (5) — (7) решается следующим образом. Сравниваем с (‑фиксировано). Если , то полагаем . При сравниваем с . Если , то полагаем и т. д. Если имеет место неравенство (сразу или после нескольких назначений линейных переменных), то ищется целочисленный минимум соответствующего квадратного трехчлена:

(A).

Обозначим через оптимальное значение . Тогда, очевидно, . Если при этом (5) не является равенством, то далее задача (5) — (7) решается как линейная (см., напр. [1]). Вторые n оптимизационных задач с одним ограничением имеют вид ( — фиксировано):

(8)

(9)

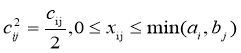, — целые(10)

Задачи вида (8) — (10) решаются вполне аналогично задачам (5) — (7).

Пусть все задач вида (5) — (7) и (8) — (10) решены. Если объединение оптимальных решений всех задач является допустимым решением исходной задачи (1) — (4), то, очевидно, тем самым получено оптимальное решение задачи (1) — (4). Если оптимальное решение задачи (1) — (4) не получено, то начинаем итерационный циклический процесс решения оптимизационных задач с двумя ограничениями.

Второй этап. Первая двумерная задача имеет вид:

(11)

(12)

(13)

— целые.(14)

Задачи вида (11) — (14) решаются следующим образом. Единственной общей переменной в (11) и (12) является . Поэтому решения задачи (11) — (14) зависят от соотношения между и другими коэффициентами в целевой функции (13). Пусть

(15)

Тогда, очевидно, что в оптимальном решении задачи (11) — (14) , после чего задача (11) — (14) распадается на две одномерные, рассмотренные выше. В этом случае определим новые значения и следующим образом. Возьмём целочисленные значения и , подчиняющиеся условиям , . Пусть,

.

Очевидно, что в этом случае , При новых значениях и объединение оптимальных решений соответствующих одномерных задач будет совпадать с оптимальным решением задачи (11) — (14). В общем случае сначала, исключив из рассмотрения общую переменную, решаются две одномерные задачи. Далее вычисляются следующие величины

.

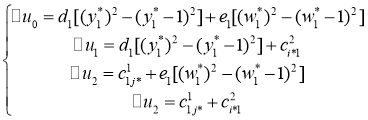Здесь , — значения переменных , в оптимальных решениях одномерных задач без , , — максимальные значения переменных при ненулевых значениях переменных в оптимальных решениях одномерных задач без . Если (или ), то в выписанных выше выражениях считаем, что (соответственно ). Вычисляется .

Если и , то двумерная задача решена. и .

Если и , то, обозначив через и значения соответствующих переменных в оптимальных решениях одномерных задач, в двумерную задачу записываются ограничения

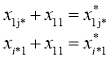
и и .

Если и , то увеличивается на (или до своего максимума). Если при этом достигает максимума, то решение двумерной задачи окончено и . В противном случае пересчитываются , k=0,1,2,3, и процесс решения продолжается. Если , то при решение двумерной задачи окончено. , .

При полагаем , .

Записываем , , . На этом решение двумерной задачи окончено. При по минимуму квадратного трехчлена находим новые значения и . Минимизация квадратного трехчлена осуществляется до наибольшего , при котором перестает быть максимумом. Далее вычисляются новые значения , и. возможно, (если новое значение ) и процесс решения продолжается.

Если , то при решение двумерной задачи окончено , .

Если , то , и записываем , . Решение двумерной задачи на этом окончено.

При по минимуму квадратного трехчлена находим новые значения и . Здесь минимизация осуществляется до наибольшего , при котором перестает быть максимумом. Вычисляются новые значения , и. возможно, (если новое значение ), и процесс решения продолжается.

Если и при решении одномерных задач мы получили и , то для нахождения новых значений и ищем минимум квадратного трехчлена

(17)

Минимизация (17) осуществляется до наибольшего целочисленного , при котором перестает быть максимумом. Глобальный минимум квадратного трехчлена (17) достигается при

(18)

Значение в (18) может оказаться дробным. Целочисленный минимум получается округлением до ближайшего целого. При полученном целочисленный минимум достигается при округлении как в большую, так и в меньшую сторону. После округления мы получаем значения и в оптимальном решении задачи (11)-(14). При этом одно из ограничений задачи (11)-(14) выйдет на равенство. Решение оставшейся одномерной задачи можно получить после вычисления новых и . Если , полученное в (18), целое или полуцелое число, то

, (19)

будут целыми числами. Рассмотрим, как можно обеспечить целочисленность итерационного процесса в общем случае. Запишем из (18) в виде

, целое.

Запишем и из (19) в виде

, ,

где , — целые числа, .

Вычислим для одномерных задач с округленными и . Квадратный трехчлен для первого ограничения имеет вид

Минимум достигается при

(20)

Квадратный трехчлен для второго ограничения

Минимум достигается при

(21)

Так как и , то из (20) и (21) получаем, что при достаточно больших и выражение и будут меньше . Таким образом, умножением всех коэффициентов целевой функции на достаточно большое число можно обеспечить целочисленность итерационного процесса.

При решение двумерной задачи окончено. , .

При в решение записываем

, , .

На этом решение двумерной задачи окончено.

, .

Так же, как и в линейном случае (см. [1]), имеет место монотонное возрастание суммы значений целевых функций в оптимальных решениях всех m+n одномерных задач в циклическом процессе решения двумерных задач и их разъединении на одномерные задачи. Сумма эта, очевидно, ограничена сверху, процесс — целочислен, следовательно, за конечное число шагов достигается предел. Точно так же, как и в линейном случае ([1]), если объединение оптимальных решений одномерных задач (в предельном состоянии) является допустимым решением исходной задачи (11) — (14), то оно является ее оптимальным решением. В противном случае, как и в [1], образуются обобщенные производители и потребители.

3. Пример Представленный алгоритм иллюстрируется следующим образом. Имеем

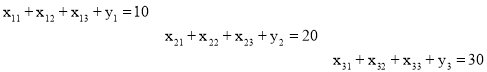
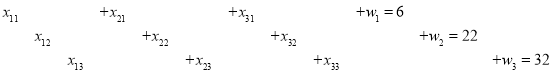
Первая одномерная задача:

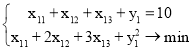
Поскольку , то . При этом может равняться как нулю, так и единице. Далее, .

Вторая одномерная задача:

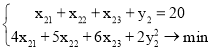
Т. к. , то ищем , и min достигается при . Таким образом , . Далее .

Третья одномерная задача:

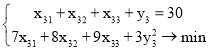
Т. к. , то ищем

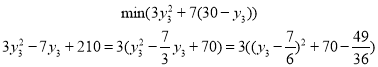
и минимум достигается при . Целочисленным минимумом, очевидно, будет при . Таким образом , . Далее, и .

Четвертая одномерная задача:

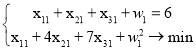
Поскольку , то . При этом может равняться как единице, так и нулю. .

Пятая одномерная задача:

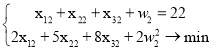
Т. к. , то . При этом может равняться как единице, так и нулю. Далее, .

Шестая одномерная задача:

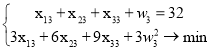
Т. к. , то . При этом может равняться как единице, так и нулю. Далее, .

Так как во второй одномерной задаче , а в четвертой — , то объединение оптимальных решений одномерных задача не является допустимым решением исходной шестимерной задачи. Следовательно, начинается циклический процесс решения двумерных оптимизационных задач.

Первая двумерная задача:

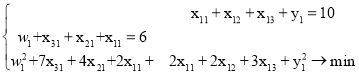
Поскольку , то, предварительно, и могут принимать значения нуль или единица. Так как , то имеем

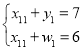
откуда . Далее, . Новые и , очевидно, остаются единицами.

Вторая двумерная задача:

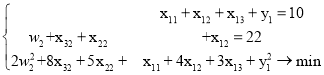
В первой одномерной задаче

Минимум достигается при и при . Так как , то и рассматривается следующий квадратный трехчлен

Минимум достигается при и при . Имеем два решения

Во второй одномерной задаче

Минимум достигается при . Так как , то и рассматривается следующий квадратный трехчлен

Минимум достигается при , следовательно, . Решение , , .

Дальнейшие вычисления начнем, используя второе решение первой одномерной задачи

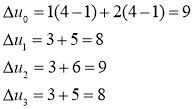
Здесь , поэтому выписываем

Минимум достигается при , поэтому , , , , . Вычисляем новые , , ,

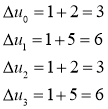
Имеем , поэтому , , , .

Вычисляем новые ,

Поскольку , то выписываем

Минимум достигается при , поэтому , , , , . Так как вышло на ограничение, то двумерная задача с первоначальным решена.

Рассмотрим решение первой одномерной задачи с

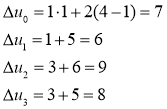
Имеем , поэтому выписываем

Минимум достигается при , однако, при уже не будет максимумом среди , поэтому пересчитываем , при . При этом ,

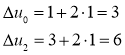
Здесь , поэтому , , .

Пересчитываем ,

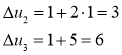
Имеем , поэтому , , .

Пересчитываем ,

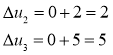
Здесь , поэтому выписываем

Минимум достигается при , однако поскольку , , . вышло на ограничение, то задача с двумя ограничениями решена. Решение:

, , , , .

Итоговые решения с первоначальными и совпали между собой.

Третья двумерная задача:

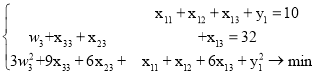
В первой одномерной задаче , .

Во второй одномерной задаче:

Минимум достигается при , следовательно, , — вышло на свой максимум, поэтому необходимо рассмотреть трехчлен

Минимум достигается при и при . Таким образом, вторая одномерная задача имеет два решения

Далее сначала используем первое решение второй одномерной задачи

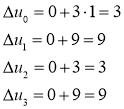
Здесь , поэтому ,

и решение запишется

и двумерная задача решена.

Четвертая двумерная задача:

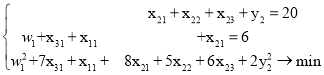
Первая одномерная задача:

Минимум достигается при . Решение , .

Вторая одномерная задача:

Минимум достигается при и при

Имеем два решения:

Далее сначала используем второе решение второй одномерной задачи

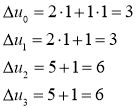
Здесь — двумерная задача решена

.

Далее (при ):

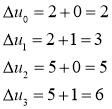
И в этом случае двумерная задача решена.

Второе решение:

, .

Пятая двумерная задача:

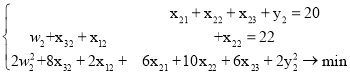
Первая одномерная задача:

Минимум достигается при и при .

Решения:

Вторая одномерная задача:

Минимум при и при , однако, так как , то необходимо рассмотреть другой трехчлен:

Минимум при . Решение:

.

Далее сначала используем первое решение первой одномерной задачи:

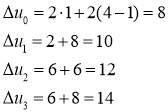
Здесь , поэтому , , .

Пересчитываем ,

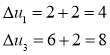
Имеем , поэтому ищем минимум трехчлена

Минимум при , следовательно,

Пересчитываем ,

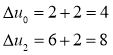
Здесь — двумерная задача решена.

Решение: .

Далее рассмотрим второе решение первой одномерной задачи:

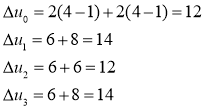
Имеем , поэтому , , .

Пересчитываем ,

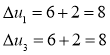
Здесь , поэтому ищем минимум трехчлена

Минимум при , следовательно,

Пересчитываем ,

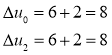
Имеем — двумерная задача решена.

Два решения:

, .

Шестая двумерная задача:

Первая одномерная задача:

Минимум достигается при и при .

Решения:

Вторая одномерная задача:

Минимум при , однако , поэтому другой трехчлен:

Минимум при и при . Решения:

Далее сначала используем первое решение первой одномерной задачи:

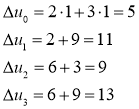
Здесь , следовательно ,, .

Пересчитываем ,

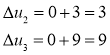
Имеем — двумерная задача решена.

Решение:

, .

Из предыдущего ясно, что существуют три других оптимальных решения:

Седьмая двумерная задача:

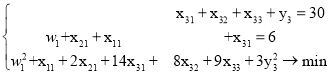
Первая одномерная задача:

Минимум достигается при и при .

Решения:

Вторая одномерная задача:

Минимум при и при . Решения:

Далее сначала используем второе решение второй одномерной задачи и первое решение одномерной задачи:

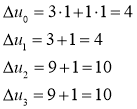
— двумерная задача решена.

Как и раньше, можем выписать все четыре оптимальных решения:

, .

Восьмая двумерная задача:

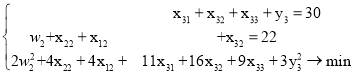
Первая одномерная задача:

Минимум достигается при и при .

Решения:

Вторая одномерная задача:

Минимум достигается при . Решение .

Далее сначала используем первое решение одномерной задачи:

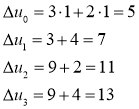
Имеем , поэтому двумерная задача решена. Решение выглядит так: . Второе решение также выписывается сразу:

.

, .

Девятая двумерная задача:

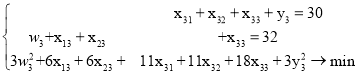
Первая одномерная задача:

Минимум достигается при . Решения:.

Вторая одномерная задача:

Минимум будет при , — решение не получено так как не выполняется равенство.

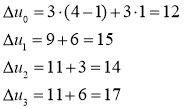
Имеем . Если положить , , то решение первой задачи можно записать в виде , а решение второй задачи — . Объединение этих решений и есть оптимальное решение двумерной задачи. На этом первый цикл решения двумерных задач окончен. На получение решения примера потребовалось три цикла решения двумерных задач. После трех циклов решения двумерных задач для одномерных задач имеем:

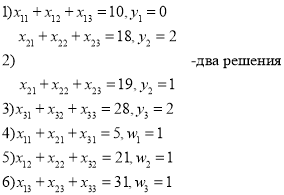
При ограничения на не сбалансированы. При ограничения на представляют собой ограничения обычной транспортной задачи. Конкретные значения можно получить методом северо-западного угла. Вот эти значения:

. Исходная задача примера решена.

4. Заключение

Итак, предлагаемый подход применим для интересного класса транспортных задач. Если рассмотреть детерминированный эквивалент двухэтапной задачи стохастического программирования со случайными векторами производства и потребления, то в случае экспоненциального распределения [7, глава 7, § 4] окончательно получается задач с квадратичным функционалом не слабых переменных. Их роль в данной работе играют переменные и . Для этого случая алгоритм также применим.

Литература:

1. Гольштейн Е. Г., Юдин Д. Б. Задачи линейного программирования транспортного типа. М.: Наука, 1969.
2. Триус Е. Б. Задачи математического программирования транспортного типа. М.: Советское радио, 1967.
3. А. П. Тизик, В. И. Цурков. Метод последовательных изменений параметров функционала для решения транспортной задачи.
4. Тизик А. П., Цурков В. И. Декомпозиционная методика для одного класса задач блочного программирования // ЖВМиМФ. 1989. т.29, № 10.
5. Тизик А. П., Цурков В. И. Оптимальное распределение каналов на сети связи // Изв. АН СССР, Техническая кибернетика. 1989. № 4
6. Думбадзе Л. Г. Разработка методов и алгоритмов в задачах оптимального использования и развития сетей. Диссертация на соискание учёной степени кандидата физико-математических наук. ВЦ РАН. М.: 2007.
7. Юдин Д. Б. Математические методы управления в условиях неполной информации. М.: Советское радио, 1974.