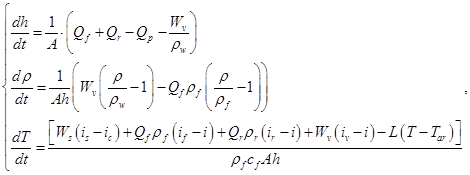Реализация замкнутого ядерного топливного цикла приводит среди прочего к необходимости обоснования технологии отработавшего ядерного топлива (ОЯТ) путем проведения исследований на экспериментальном и опытно-промышленном оборудовании. При этом создание эффективного радиохимического производства с учетом его высокой радиационной, ядерной и экологической опасности невозможно без использования систем автоматического управления (САУ) [1].
В технологиях переработки ОЯТ для кондиционирования растворов зачастую применяют метод непрерывного упаривания — кондиционирование жидких отходов, концентрирование целевых продуктов в линии урана. Поэтому обеспечение эффективного непрерывного режима цепи технологических переделов будет зависеть от работы выпарного оборудования. Существенным его отличием от аналогичных аппаратов является малый объем вследствие относительно небольшого масштаба производства в защитном исполнении и обеспечения ядерной безопасности [1].
Сложность разработки САУ подобными аппаратами определяется среди прочего многосвязностью, существенной нелинейностью по отдельным каналам управления, а также отсутствием самовыравнивания. Поэтому для проведения вычислительных исследований возможных вариантов САУ однокорпусным выпарным аппаратом (ВА) с вынесенной греющей камерой, предназначенным для упаривания азотнокислого раствора уранилнитрата (см. Рис. 1), необходимо создать его математическую модель, описывающую динамические связи между основными технологическими переменными. При этом, согласно общепринятому в инженерной практике правилу, для синтеза САУ из-за приближенного характера формул аналитического расчета параметров настройки регуляторов вполне достаточно 10 %-ой точности модели [2].
Математическая модель процесса упаривания реэкстракта урана должна отражать:
– динамику изменения уровня раствора в аппарате в зависимости от расходов исходного раствора реэкстракта урана, упаренного реэкстракта урана, флегмы и расхода греющего пара;
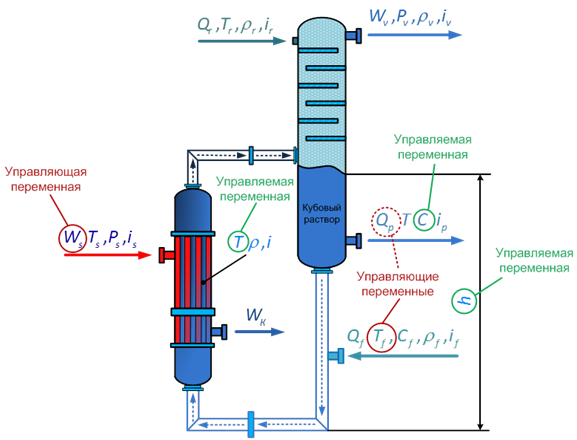
Рис. 1. Схема выпарного аппарата: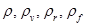 
— соответственно плотность раствора в аппарате, вторичного пара, флегмы, исходного раствора реэкстракта урана, кг/м3; 
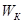— массовый расход конденсата, кг/ч; 
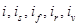— соответственно энтальпия раствора в аппарате, греющего пара, входного раствора, флегмы и вторичного пара, Дж/кг
– динамику изменения концентрации/плотности упаренного раствора в зависимости от расхода и концентрации/плотности исходного раствора и флегмы, расхода упаренного реэкстракта урана и греющего пара;
– динамику изменения температуры раствора в аппарате в зависимости от температур исходного раствора, флегмы, греющего пара и давления на линии подачи пара в греющую камеру.
Кроме этого, модель должна учитывать взаимное влияние друг на друга перечисленных выше, выходных контролируемых параметров объекта.
Так как априорная информация о термодинамических свойствах упариваемого продукта, физических и термодинамических параметрах греющего и сокового пара, а также необходимых данных для описания тепловых потерь в окружающую среду и т. д. отсутствовала, то потребовалось существенно упростить математическое описание.
В результате динамика материальных, элементных и тепловых потоков в аппарате описывается следующей системой уравнений:
где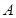 
— площадь поперечного сечения ВА, м2;
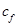— удельная теплоемкость входного раствора, кДж/(°C×кг);
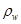— плотность воды, кг/м3, а массовый расход вторичного пара 
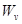определяется по следующему алгебраическому выражению:
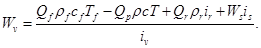
Энтальпии греющего, вторичного пара и конденсата определяются по выражению, полученному путем аппроксимации табличных данных:
.
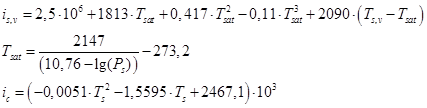Разработанный подход и математическое описание выпарного аппарата как объекта управления было реализовано в виде компьютерной модели в пакете MATLAB/Simulink. Для проверки качественной адекватности модели использовались результаты исследований выпарных аппаратов, приведенных в работе [7], где в качестве одного из объектов исследования использовалась двухступенчатая вакуум-выпарная установка «Единство».
На рисунке 2 представлены переходные характеристики по уровню во втором аппарате установки «Единство», при изменении расхода питающего раствора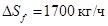 
в аппарат на 62 % и соответствующий переходный режим в разработанной модели аппарата упаривания реэкстракта урана.
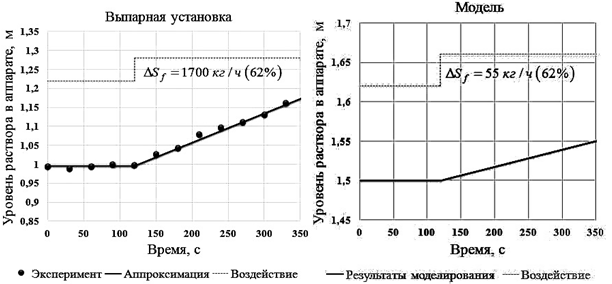
Рис. 2. Переходные процессы по уровню
Как видно из графиков, характер изменения уровня в обоих случаях идентичен, и данный канал объекта управления можно описать астатическим звеном.
На рисунке 3 представлены переходные характеристики по концентрации в первом аппарате установки «Единство», при изменении расхода жидкости на выходе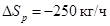 
из аппарата на –30 % и соответствующий переходный режим в разработанной компьютерной модели ВА.
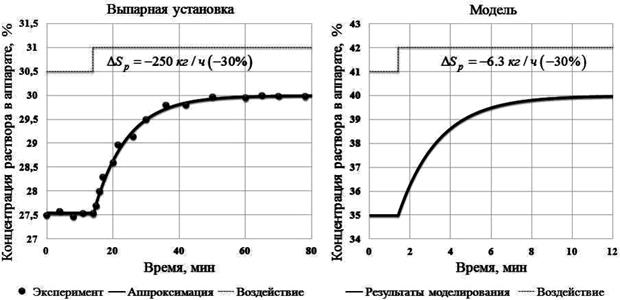
Рис. 3. Переходные процессы по концентрации
Вышеприведённые графики показывают, что переходные процессы, по концентрации, полученные на выпарной установке и в результате моделирования, совпадают на качественном уровне. Кроме того, можно заметить, что объект по данному каналу можно описать апериодическим звеном первого порядка.
На рисунке 4 представлены переходные характеристики по температуре раствора в первом аппарате установки «Единство», при изменении расхода греющего пара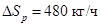 
из аппарата на 17 % и соответствующий переходный режим в разработанной компьютерной модели ВА.
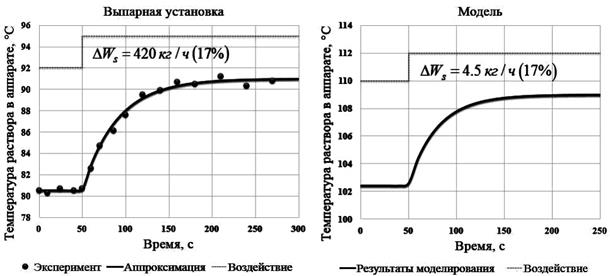
Рис. 4. Переходные процессы по температуре
Вышеприведённые графики показывают, что переходные характеристики по температуре, полученные на выпарной установке и в результате моделирования, совпадают на качественном уровне. Кроме того, можно заметить, что объект по данному каналу, так же как по концентрации, можно описать апериодическим звеном первого порядка.
Сравнение результатов моделирования с данными [8] показывает их качественное совпадение.
Анализ вышеприведённых переходных процессов показывает, что постоянная времени выпарных аппаратов по концентрации/плотности, существенно выше постоянных времени по уровню и температуре. Данное обстоятельство необходимо учитывать при разработке САУ выпарным аппаратом.
Проверка количественной адекватности разработанной модели проводилась по экспериментальным данным, полученным на лабораторном выпарном стенде НПО Радиевый институт имени В. Г. Хлопина, г. Санкт-Петербург.
Данный стенд оснащен автоматизированной системой управления, в основе которой заложены два алгоритма управления.
Первый алгоритм предназначен для режима упаривания с заданной кратностью. При этом уровень кубового раствора поддерживался постоянным за счет регулирования расхода исходного раствора. В нестационарном режиме (до достижения заданной плотности раствора) кубовый раствор не сливался. В непрерывном режиме раствор сливался в пропорциональном среднему расходу исходного раствора количестве.
Второй алгоритм обеспечивал заданную плотность раствора на выходе выпарной установки в непрерывном режиме. Подержание заданной плотности кубового раствора осуществлялось расходом исходного раствора, а подержание уровня — сливом кубового раствора.
На установке был проведен следующий эксперимент. В режиме пуска ВА после его первоначального заполнения исходным раствором и начала процесса выпарки управление процессом шло по первому алгоритму в нестационарном режиме. После достижения заданной величины плотности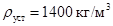 
, то есть выхода объекта на стационарный режим, управление осуществлялось по второму алгоритму. Если измеренная плотность кубового раствора была больше величины 
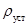, то задавался максимальный расход исходного раствора, если меньше — устанавливался минимальный расход. То есть управления осуществлялось по релейному закону.
После выхода на стационарный режим был зафиксирован переходный процесс при изменении уставки регулятора плотности от 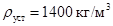, до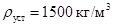 
.
Аналогичный эксперимент был проведен на разработанной компьютерной модели выпарного аппарата. Экспериментальные данные и результаты моделирования приведены на рисунке 5а.
На стенде был проведен еще один эксперимент, в котором после достижения заданной величины плотности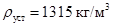 
ее уменьшили до значения 
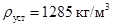. Результаты эксперимента приведены на рисунках 5б–5г.
Относительные среднеквадратичные погрешности воспроизведения уровня, плотности и температуры раствора, составили менее 9 %, 5 % и 7 % соответственно, что удовлетворяет предъявленным требованиям.
Таким образом, в ходе работы была подтверждена качественная и количественная адекватности разработанной компьютерной модели, что позволяет использовать ее при разработке САУ ВА.
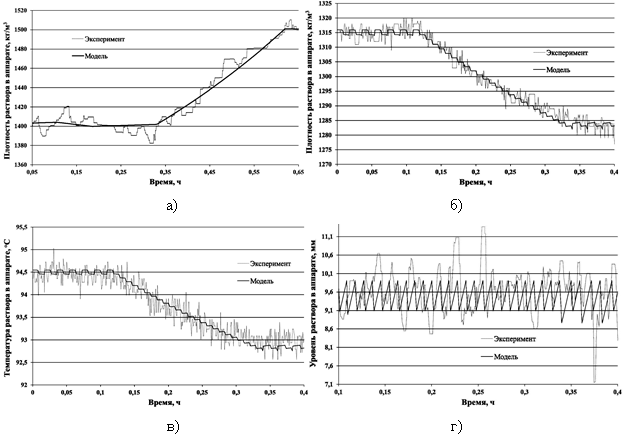
Рис. 5. Переходные процессы по плотности (а, б), по температуре (в) и по уровню (г) в лабораторном выпарном стенде и компьютерной модели
Литература:
1. Автоматическое управление выпарным оборудованием в технологиях переработки отработанного ядерного топлива / И. Ю. Шевяков, К. А. Козин, А. Г. Горюнов, Ф. Э. Гофман, Б. Я. Зильберман, Д. В. Рябков // VI Междунар. научно-практ. конф. «Физико-технические проблемы атомной науки, энергетики и промышленности»: сб. тез. докл. / Томский политехн. ун-т. — Томск, 2014. — С. 52.
2. Советов Б. Я., Яковлев С. А. Моделирование систем: Учебник для вузов. — 2-е издание. — М.: Высшая школа, 1998. — 319 с.
3. Кафаров В. В., Глебов М. Б. Математическое моделирование основных процессов химических производств: Учеб пособие для вузов. — М.: Высш. шк., 1991. — 400 с.
4. Луценко В. А., Финякин Л. Н. Математическое моделирование химико-технологических процессов на аналоговых вычислительных машинах. Лабораторно-практические работы. — 2-е изд. перераб. и доп. — М.: Химия, 1984 — (серия «Химическая кибернетика»). — 272 с.
5. Луценко В. А., Финякин Л. Н. Аналоговые вычислительные машины в химии химической технологии. — 2-е изд. перераб. и доп. — М.: Химия, 1979 — (серия «Химическая кибернетика»). — 248 с.
6. Самарский А. А., Михайлов А. П. Математическое моделирование: Идеи. Методы. Примеры. — 2-е изд., испр. — М.: Физматлит, 2001. –320 с.
7. Таубман Е. И. Расчет и моделирование выпарных установок. — М.: Химия, 1970. — 216 с.
8. Kiew M. Kam, Prabirkumar Saha, Moses O. Tadel, G. P. Rangaiah. Models of an Industrial Evaporator System for Education and Research in Process Control // Developments in Chemical Engineering and Mineral Processing. — 2002. –V. 10. — № 1–2. — P. 105–127.
