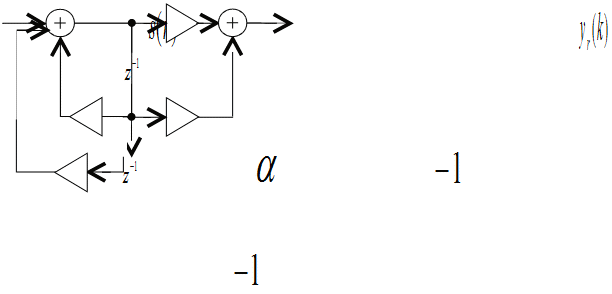Математическая модель формирования радиотелефонного канала для передачи аудиоинформации

Согласно концепции устойчивого развития сельских территорий Российской Федерации на период до 2020 года, опубликованной центром экономической безопасности Российской Федерации [1, с.30] необходимо обеспечить телефонизацию всех сельских населенных пунктов и объектов социальной сферы. Однако прокладка проводных линий связи невозможна в силу действующих экономических или технических ограничений[2].

В этой связи актуальна задача телефонизации объектов хозяйственной деятельности, расположенных в местности, где отсутствуют проводные телефонные линии связи абонентов. Передача аудио информации может быть основана на развёртывании на объекте систем абонентского радио доступа. Одним из вариантов решения задачи является интеллектуальный радиоудлинитель телефонной линии, математическая модель которого предлагается к рассмотрению.

Радиоудлинитель телефонной линии включает в себя абонентский и базовый блоки, которые находятся на значительном удалении друг от друга. К базовому блоку непосредственно подключаются, имеющиеся проводные телефонные линии. Абонентский блок подразумевает непосредственное подключение стандартных телефонных аппаратов. Базовый и абонентский блоки радиоудлинителя взаимодействуют через радио канал связи посредством стандартных серийно выпускаемых радиостанций, что позволяет не ограничивать частотный диапазон канала. Устройство работает в дуплексном радиоканале с разнесёнными частотами. Для предотвращения несанкционированного использования канала в устройстве предусмотрена взаимная аутентификация блоков устройства. Логика работы радиоудлинителя не подразумевает использование нестандартных сигналов для взаимодействия с телефонной линией. Радиоудлинитель ретранслирует стандартные сигналы от автоматических телефонных станции к абоненту и обратно. Радиоудлинитель телефонной линии позволяет работать с несколькими телефонными линиями одновременно. Интеллектуальный радиоудлинитель телефонной линии выполняет непосредственный перенос функций проводной телефонных линий посредствам дуплексного радиоканала [2]. Необходимо построить математическую модель устройства, для того, чтобы получить представления о процессах, происходящих при передаче аналоговой информации описанным выше радиоудлинителем, посредством математического описания.

Общая цель моделирования может быть сформулирована, как расчёт значений передаваемого аудио информационного сигнала по времени в радиоканале с учётом влияния факторов внешней среды. Цель моделирования указанной системы состоит в теоретическом изучении процесса установления связи между блоками и передачи аудиоинформации при заданных условиях внешней среды, а также внутренних служебных процессов коммутации внутри блоков системы. Необходимо установить математические и аналитические зависимости между параметрами аудио информации, приближенно описывающими поведение системы. Установить последовательность применения уравнений и вычисления параметров их составляющих.

Данная модель актуальна, в связи с необходимостью показать общую структуру детерминированных сигналов, передача которых является непосредственной задачей радиоудлинителя, принцип действия которого заключается в перенесении свойств удалённой телефонной линии к телефонному аппарату абонента посредством дуплексного радио канала [2], установить законы их взаимодействия, влияния внешней среды для того, чтобы уточнить способы управления формированием и передачей таких сигналов при заданных условиях внешней среды. Для достижения последнего над математической моделью проводят численные эксперименты, то есть исследования характера изменения параметров объекта во времени при применении его модели, что в свою очередь позволяет наглядно представить результаты и установить между ними зависимости. Последние представляют собой расстояние между объектами, накладываемые на детектирование сигналов ограничивающие соотношения сигнал-шум. демонстрирующие, в свою очередь, влияние шума на полезный сигнал, а также условия ограничивающие поведения сигнала при его модулировании, нарушение которых может привести к его последующей перемодуляции. Также модель позволит спрогнозировать прямые и косвенные последствия реализации заданных способов воздействия на объект, с учётом изменений отдельных параметров полезного сигнала и ограничивающих факторов передачи[4].

Авторами планируется поэтапное построение модели. Таким образом, составная модель системы должна включать в себя приведённую в статье аналитическую модель аналоговой части разработанного устройства, модель цифровой части, отвечающий за управление коммутацией частей устройства, а также имитационная модель системы в виде программы для электронной вычислительной машины на одном из распространённых языков программирования.

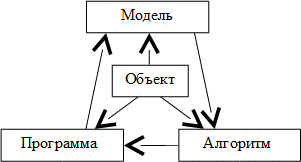
Построение данной модели соответствует процессу планирования построения модели, представленного с помощью функциональной схемы [3, с. 7], приведённой на рисунке 1.

Рисунок 1 – функциональная схема планирования процессам моделирования

Как показано на рисунке 1, постановка вопроса о моделировании какого-либо объекта или процесса включает их формализацию, алгоритмизацию и непосредственное составление и отладку программы. Под формализацией понимается построение математической модели [4, с.33].

Рассмотрим, как исследуемый объект взаимодействует с внешней средой. Объект имеет свойство непрерывно усложняться, то есть является сложной системой различных компонент, взаимосвязанных друг с другом. Примем системный подход к созданию модели, при котором необходимо выделить систему S и внешнюю среду E [4, с. 21]. При этом модель также является системой S’ = S’(M), рассматриваемой относительно внешней среды E [4, с.22]. Структура системы приведена на рисунке 1.

В качестве внешней среды E в данном случае рассматривается физический уровень передачи данных, включающий среду передачи данных, а также элементы передачи данных, состоящие из радиопередающих устройств и антенн. Таким образом, внешняя среда E объективно находится вне исследуемой системы, а, следовательно, и модели данной системы, одновременно находится под воздействием системы и оказывает влияние на неё [4, c.20].

На основании данных о внешней среде построена аналитическая модель и выявлены ограничения для построения системы [4, с. 24]. Влияние модели внешней среды E’, носит ограничивающий характер в виде рекомендуемых параметров элементов передачи данных, достаточных для функционирования системы с целью решения задач построения устройства радиоудлинения [2]. Также обратимся к натурному моделированию, когда данные полученные с помощью модели адекватны реальному объекту. Таким образом, в данном случае, кроме математического, имеет место также натурное моделирование, то есть проведение исследования на реальном объекте с последующей обработкой результатов эксперимента на основе теории подобия [4, с. 36], являющейся основанием теории моделирования [4, с.31].

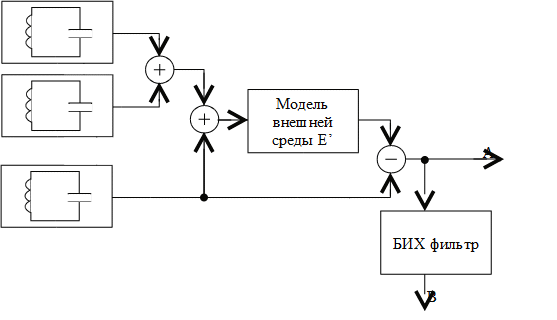
Элемент аналоговой коммутации предназначен для формирования аудио канала связи [2], что указывает на колебательный характер процессов, происходящих в последнем. Сказанное верно и для элемента аутентификации, с той разницей, что аутентификация производится с помощью двухтональных многочастоных сигналов (DTMF) [2]. Очевидно, что элементы аутентификации и аналоговой коммутации, в общем случае, представляют собой источники колебаний, в пределах модели для них могут быть определены сходные функции, поэтому в качестве основы для количественной и качественной описательной оценки происходящих в устройстве процессов, то есть в качестве модели, устройства, подходит колебательный LC-контур [3, с.50]. В силу сложности описания сложных голосовых сигналов, ограничимся моделью через колебательный электрический процесс, который основан на фундаментальных законах природы. Отстроение моделей с использованием фундаментальных законов природы является распространённым методом построения моделей [3, с. 11]. В силу того, что таковые законы общепризнанны, подтверждены опытом, их обоснованность не вызывает сомнений, они актуальны для построения всех математических моделей [3, с. 11]. Cоставим функциональную схему математической модели. Функциональная схема модели аналоговых процессов системы приведена на рисунке 2.

Рисунок 2 – Функциональная схема модели аналоговых процессов описываемой системы

Уравнение, описывающее колебательный процесс в одном из простейших электрических колебательных контуров через изменение значений тока и напряжения [3, с.50], изображённых на рисунке 2, следующее (1):

(1)

– значение индуктивности контура,

– дифференциал, описывающей значения силы тока в системе по времени,

– функция изменения напряжения.

Уравнение (3) справедливо для каждого из электрических колебательных контуров модели, приведённой на рисунке 3, однако, каждый из колебательных контуров имеет собственную частоту колебаний, поэтому переменные равенств

Для математического моделирования сложного сигнала в системе, состоящего из нескольких частот необходимо сложить сигналы двух контуров модели, изображённой на рисунке 2, таким образом, получим равенство (2):

(2)

Таким образом, получим сложный сигнал, который для упрощения восприятия запишем в виде уравнения (3):

(3)

Уравнение (9) представляет в модели сложный аналоговый сигнал, который должен быть промодулирован [5]. Промодулируем сложный основной сигнал, описанный в выражении (3), получим следующее уравнение для модулированного сигнала (4):

(4)

Для детектирования сигнала необходимо учесть соотношение сигнал-шум [5, с.175], по следующей формуле (5):

, где (5)

– соотношение сигнал-шум

– мощность сигнала,

– коэффициент, учитывающий амплитуду шумов и ширину полосы частот.

Для целей данной модели учитываем, что приёмо-передающий элемент, изображённый на рисунке 2, генерирует только гауссовы шумы с амплитудой . Мощность сигнала является ограничением, накладываемым внешней средой и имеет квадратичную зависимость от расстояния[6, с. 178], запишем выражение для мощности передаваемого сигнала (6):

, где (6)

– суммарная мощность сигнала,

– мощность передатчика в момент приёма абонентом сигналов, для данной модели примем ,

– коэффициенты, определяющие усиление сигнала в направлении к приёмнику и от него, для целей данной модели примем равными единице, для данной модели считаем ,

– длина волны, аналогично выше сказанному,

– расстояние между приёмо-передающими элементами среды E, изображёнными на рисунке 2, поскольку расстояние между приёмо-передающими подсистемами объекта в реальности не изменяется, то считаем .

Уравнение (7) для определения соотношения сигнал-шум модели внешней среды E’ модели выглядит следующим образом:

(7)

БИХ фильтр или фильтр с бесконечной импульсной характеристикой в данной модели предназначен для имитации устройств, ответственных за распознавание двухтональных многочастотных сигналов набора номера, и работает по алгоритму Герцеля, подробно описанному в публикации [7], структурная схема описанного БИХ фильтра приведена на рисунке 3.

Значение (8) вещественного коэффициента для схемы на рисунке 3 [7]:

, где (8)

- номер спектрального отсчёта,

- количество точек преобразования.

Для схемы изображённой на рисунке 3, значение S(k) определяется уравнением (9):

, где (9)

– комплексные отсчёты спектра по Фурье,

– поворотные коэффициенты, обладающие следующим свойством: при .

Рисунок 3 – структурная схема БИХ фильтра Герцеля

В уравнении (9) промежуточные значения и рассчитываются итерационно по формуле (10):

(10)

Поворотные коэффициенты уравнения (9) имеют реальную часть и мнимую части. С учётом последних исчисляются реальная и мнимая части спектральных отсчётов.

Алгоритм Герцеля сводится к итерационному расчёту по формуле (10), где последние итерационные значения помещаются формулу (9) для окончательного пересчёта спектрального отсчёта .

Очевидно, что реальные и мнимые части поворотного коэффициента уравнения (9), а также коэффициент уравнения (10) опираются на характер сигнала. В связи этим необходимо для электромагнитного колебательного процесса конкретизировать форму колебательного сигнала.

Так уравнение (11) сложного колебательного процесса следующее:

(11)

– функция изменения величины напряжения,

– максимальное (амплитудное) значение ,

– угловая частота или ,

– сдвиг фаз.

Уравнение(12) модулированного сигнала следующее:

(12)

Приведём ограничения для системы уравнений. Выше было замечено, что влияние модели внешней среды E’, носит ограничивающий характер. Приведём ограничение (13) распространения сигнала по формуле (7), обозначив максимальное значение полезного сигнала, как , паразитного как .

(13)

Отношение полезного сигнала к значению шумов должно быть достаточно велико [5, с.178].

Выражение , аналогично и выражение , для чего необходимо выполнение условий , и , иначе возникнет перемодуляция сигнала, то есть избыточная модуляция, демодуляция такого сигнала приведёт к его искажениям [5, с.136].

Коэффициент для уравнения (10) должен изменяться по закону (8), также при моделировании по алгоритму Герцеля нужно учесть мнимые и реальные части. Таким образом, имеем системы аналогичных уравнений для сигнала с аналогичной системой ограничений.

Система уравнений (14), описывающая характеристики колебательного сигнала модели во времени выглядит следующим образом:

,

, (14)

,

;

Приведём систему ограничений для системы уравнений (14), ограничения вызваны присутствием материальных объектов, составляющих внешнюю среду E системы, непосредственно не входящих в модель [5, с. 99]. Соответствующая системе уравнений (14) система ограничений (15) выглядит следующим образом:

,

, (15)

;

Для конкретизации описания формы колебательного сигнала LC-контура модели приведём следующую систему уравнений (16), описывающих гармоническую составляющую сигнала:

,

, (16)

,

;

Соответствующая ей система ограничений (17) выглядит следующим образом:

,

, (17)

,

;

Приведём систему уравнений (18) для описания подсистемы, моделирующего обработку сигнала на принимающей стороне:

, (18)

;

Система ограничивающих условий (19) для данной системы следующая:

,

,

, (19)

,

;

Приведённая математическая модель приближенно описывает процессы передачи информации для устройства интеллектуального радиоудлинителя телефонной линии [2]. Модель адекватна реализации полезной модели радиоудлинителя телефонной линии [2] с некоторой степью приближения, что позволяет оценить параметры передаваемых сложных сигналов по времени и по форме и вычислить их при различных начальных условиях. Аналитическая модель учитывает с некоторой степенью приближения помехи внешней среды (соотношение сигнал-шум) [6, с. 175], влияющие на распространение сигнала, расстояние между подсистемами. Вышесказанное позволяет проводить с использованием модели эксперименты с целью прогнозирования возможных условий передачи, оценки параметров генерации и анализа сигналов. Модель позволяет вести расчёт по параметрам передаваемых сигналов, даёт возможность рассчитывать показатели по комплексным отсчётам спектра сигнала при анализе, прогнозировать прямые и косвенные последствия реализации заданных способов воздействия на объект, с учётом изменений отдельных параметров полезного сигнала и ограничивающих факторов передачи. Модель адекватна реальному объекту и с определённой степенью приближения процесс его функционирования во внешней среде E [4, с. 88]. Основой модели служат фундаментальные законы природы [3, с.11]. В приведённой математической модели, при заданных условиях внешней среды, установлены математические и аналитические зависимости между параметрами аудио информации, приближенно описывающими поведение описанной выше системы, установлена последовательность применения уравнений и вычисления параметров их составляющих в виде систем уравнений (14)-(18).

Литература:

1. Концепция устойчивого развития сельских территорий Российской Федерации на период до 2020 года // Центр экономической безопасности [Электронный ресурс]

2. Чегодаев, Н.И. Проблематика научных исследований в области телефонизации удалённых объектов хозяйственной деятельности [Текст] / Н.И.Чегодаев // Молодой учёный – 2011. - №9 – С.61-64.

3. Самарский, А.А. Математическое моделирование: Идеи. Методы. Примеры [Текст] / А.А.Самарский, А.П.Михайлов – Физматлит, 2009 – 320 с.

4. Советов, Б.Я. Моделирование систем [Текст] / Б.Я.Советов, С.А.Яковлев – М.: Высшая школа, 2010 – 343 с.

5. Рид, Р. Основы теории передачи информации [Текст] / Р.Рид – Вильямс, 2007 – 304 с.

6. Мельник, Ю.А. Основы радиотехники и радио-технические устройства [Текст] / Ю.А.Мельник, Г.В.Стогов – М.: «Радио», 1978– 368с.

7. Алгоритм Герцеля // Теория и практика обработки сигналов [Электронный источник] – режим доступа: http://www.dsplib.ru/content/goertzel/goertzel.html