Параллельный вычислительный алгоритм для анализа акустических волн в жидком кристалле с учетом моментных взаимодействий



Параллельный вычислительный алгоритм для анализа акустических волн в жидком кристалле с учетом моментных взаимодействий

Смолехо Ирина Владимировна, аспирант

Институт вычислительного моделирования СО РАН (г. Красноярск)

Введение

Жидкий кристалл – это промежуточное агрегатное состояние вещества, в котором проявляются одновременно свойства упругости и текучести. Жидкокристаллическая фаза образуется при плавлении ряда органических веществ. Она существует в интервале от температуры плавления до некоторой более высокой температуры, при нагреве до которой вещество переходит в обычную жидкость. Подобно жидкости этот кристалл может принимать форму сосуда, в который он помещен. Однако кроме этого свойства, объединяющего его с жидкостями, он обладает наличием порядка пространственной ориентации молекул, характерным для кристаллов. В зависимости от вида упорядочения осей молекул жидкие кристаллы разделяются на три разновидности: нематические, смектические и холестерические.

Один из подходов к построению математических моделей для описания поведения жидких кристаллов основывается на представлении о жидкокристаллической среде как о мелкодисперсной сплошной среде, в каждой точке которой домены жидких кристаллов могут перемещаться в соответствии с законами динамики вязкой или невязкой жидкости и вращаться, проявляя упругие свойства. Модели жидкого кристалла были предложены Эриксеном [1], Лесли [2], Аэро [3] и другими авторами.

Данная работа посвящена численному решению дифференциальных уравнений второго порядка для касательного напряжения и угловой скорости, полученных из системы уравнений, описывающей термомеханическое поведение жидкого кристалла.

Математическая модель

Основная система уравнений жидкого кристалла при слабых акустических возмущениях с учетом моментных напряжений в двумерном случае выглядит следующим образом [4–6]:

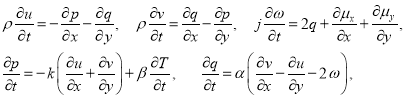(1)

Здесь и – компоненты вектора скорости; – угловая скорость; – угол поворота молекул кристалла; – гидростатическое давление; – касательное напряжение; и – моментные напряжения; – абсолютная температура; – плотность; – момент инерции; – модуль объемного сжатия; – модуль упругого сопротивления вращению; – коэффициент теплового расширения; – удельная теплоемкость; , и – пространственные переменные и время; и – коэффициенты теплопроводности в направлении ориентации молекул жидкого кристалла и в поперечном направлении; , и – компоненты симметричного тензора теплопроводности: , , . В систему (1) входят уравнения поступательного и вращательного движений, уравнение для угла поворота, уравнения состояния для давления и касательного напряжения, уравнение анизотропной теплопроводности с переменными коэффициентами. Параллельный вычислительный алгоритм для решения системы уравнений жидкого кристалла без учета моментного воздействия подробно описан в [7].

Рассмотрим, как из системы (1) получается система уравнений второго порядка для касательного напряжения и угловой скорости. Продифференцировав первое уравнение системы (1) по , а второе по , и, сложив результаты, получим:

.

Затем продифференцируем уравнение для давления по :

.

Далее первое уравнение системы (1) продифференцируем по , а второе по . После вычитания имеем:

.

С учетом этого выражения после дифференцирования соответствующих уравнений системы (1) по , получим отдельную подсистему для касательного напряжения и угловой скорости :

, .

Начальные данные для системы (2) выглядят следующим образом:

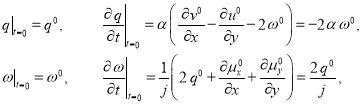(3)

где , , , ,, – заданные в начальный момент времени константы.

Из подсистемы (2) можно вывести уравнение четвертого порядка для . Выразив из первого уравнения и подставив во второе, продифференцированное по , получим:

.

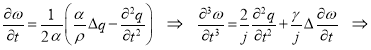
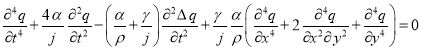Начальные данные для соответствующей задачи Коши таковы:

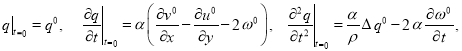
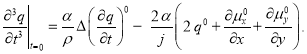
Численный алгоритм

Для решения системы уравнений второго порядка (2) разработан численный алгоритм. Искомыми величинами являются касательное напряжение и угловая скорость внутри расчетной области. Используются начальные данные вида (3). Граничные условия задаются в терминах , , а также , и , . Применяется явная конечно-разностная схема “крест” второго порядка аппроксимации по , и . Уравнения системы (2) на каждом временном слое аппроксимируются заменой производных по времени и пространству конечными разностями:

,

.

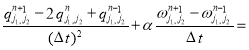
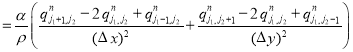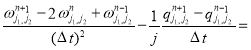
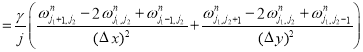Здесь и . Далее из второго уравнения выражается :

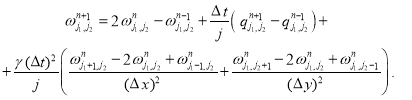(4)

После подстановки (4) в первое уравнение получается формула для расчета :

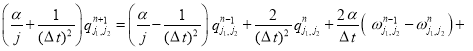
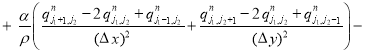(5)

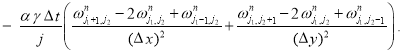
Таким образом, на новом слое по времени нужно сначала решать уравнение (5) для , а затем уравнение (4) для при заданных начальных данных и граничных условиях.

Исследование устойчивости схемы

Пусть точное решение конечно-разностной схемы выглядит следующим образом:

, .

Подставим его в первое уравнение системы (2):

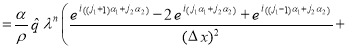
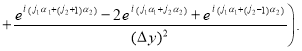
После деления обеих частей уравнения на (), получим:

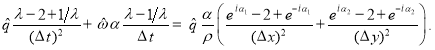
Упростим выражение

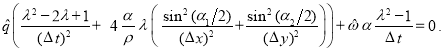
Проведя аналогичные выкладки для второго уравнения системы (2), получим:

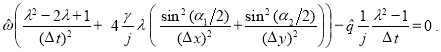
Для получения характеристического уравнения составим матрицу из коэффициентов при и :

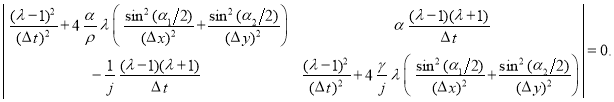
Введя обозначения

, , , ,

вычислим определитель

,

.

Далее рассмотрим три случая при разных значениях , и :

1). Если , то , ,

, , , .

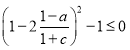Следовательно, в этом случае получим условие устойчивости :

.

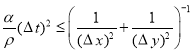2). Если , то , и аналогично предыдущему случаю, получим, что . Условие устойчивости выглядит следующим образом:

.

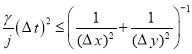3). Если , то . Сделав замену , получим

, , , ,

, , .

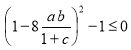Последнее условие выполняется автоматически. Условие означает, что

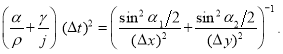
При таком выборе шага для заданных значений и .

В общем случае получается следующее условие устойчивости:

.

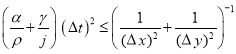Параллельная программа

Описанный выше алгоритм для численного решения системы уравнений (2) по формулам (4), (5), реализован в виде параллельной программы. Она написана на языке Си с применением технологии CUDA, которая позволяет существенно увеличить вычислительную производительность благодаря использованию графических ускорителей видеокарт. GPU (Graphical Processing Unit) ориентирован на выполнение программ с большим объемом вычислений. За счет большого количества параллельно работающих процессорных ядер, обычный компьютер превращается в суперкомпьютер со скоростью вычислений в сотни раз выше, чем ПК, использующий лишь вычислительную мощность центрального процессора (CPU).

Все вычисления производятся на GPU. Расчетная область разбивается на квадратные блоки, содержащие одинаковое количество нитей. Каждый блок представляет независимый набор взаимодействующих между собой нитей, которые из разных блоков не могут взаимодействовать между собой. Благодаря идентификаторам, имеющимся в CUDA, каждой нити ставится в соответствие ячейка разностной сетки. В параллельном режиме нити графического устройства выполняют однотипные операции в ячейках по расчету решения.

Параллельная программа имеет следующую структуру:

–задание размерностей конечно-разностной сетки и всех используемых констант (на CPU);

–описание одномерных массивов для касательного напряжения и угловой скорости (на CPU);

–задание начальных данных для этих величин в узлах конечно-разностной сетки (на CPU);

–описание событий start и stop для замера времени выполнения программы на GPU, начало замера времени, начало параллельной части работы программы;

–копирование необходимых для расчетов констант из CPU в GPU;

–описание массивов для угловой скорости и касательного напряжения, а также для всех необходимых вспомогательных величин, выделение под них памяти (на GPU);

–копирование данных из CPU в GPU (массивов искомых величин);

–задание переменных типа dim3 для количества блоков в сетке и количества нитей в каждом из таких блоков (на GPU);

–основной расчетный цикл по времени, в котором последовательно выполняются процедуры-ядра (на GPU):

–задание граничных условий в направлении ,

–задание граничных условий в направлении ,

–решение системы уравнений для касательного напряжения и угловой скорости с помощью конечно-разностной схемы “крест”,

(после выполнения ядер производится барьерная синхронизация, чтобы обеспечить завершение вычислений каждой нитью до начала выполнения следующих вычислений);

–копирование результатов счета из GPU в CPU (массивов угловой скорости и касательного напряжения) в контрольных точках (на некоторых шагах по времени);

–освобождение памяти переменных на GPU;

–окончание замера времени работы на GPU, печать этого времени, уничтожение событий start и stop, завершение параллельной части работы программы;

–освобождение памяти переменных на CPU, завершение работы программы.

Результаты расчетов

Для демонстрации работы параллельной программы выполнена серия расчетов на высокопроизводительном вычислительном сервере Flagman с графическими вычислителями Tesla C2050 в Институте вычислительного моделирования СО РАН (общее число потоковых ядер CUDA на сервере – 3584).

Расчеты проводились для жидкого кристалла 5ЦБ со следующими параметрами: кг/м³, кг/м, ГПа, Н.

На рис. 1 приведены линии уровня касательного напряжения в разные моменты времени для задачи с начальными данными:

, , ,

и нулевыми граничными условиями . Расчеты проведены на квадратной области 100 мкм 100 мкм. Размерность конечно-разностной сетки 10241024 ячеек.

Рис. 1. Заданная начальная угловая скорость : линии уровня

касательного напряжения (1000-й, 2500-й и 4000-й шаги по времени)

На рис. 2 представлены результаты расчетов для задачи о действии трех П-образ-ных импульсов касательного напряжения на частях боковых границ расчетной области. Время действия каждого импульса и промежуток времени между ними 8 нс. Заданы нулевые начальные данные. Граничные условия на левой и правой границах: , если ; и , если ; . Здесь – центр зоны, где действует нагрузка, – радиус этой зоны. В расчетах мкм, мкм. На верхней и нижней границах заданы условия периодичности. Расчеты проведены на прямоугольной области 100 мкм 40 мкм. Размерность сетки 25601024 ячеек.

Рис. 2. Три П-образных импульса касательного напряжения на боковых границах: линии уровня касательного напряжения (1000-й, 3000-й и 3500-й шаги по времени)

На рис. 3 приведены результаты для задачи о периодическом действии касательного напряжения на части границы. Граничные условия на нижней границе: , если ; и , если ; . Верхняя граница закреплена, на боковых заданы условия периодичности. Частота в расчетах принималась равной , где – период осцилляций, и . Размерность сетки 20481024 ячеек.

Рис. 3. Периодическое действие касательного напряжения: линии уровня угловой скорости

( и , 4000-й шаг по времени)

Заключение

В рамках акустического приближения модели жидкого кристалла получена система уравнений второго порядка для касательного напряжения и угловой скорости с учетом моментных взаимодействий. Разработан алгоритм численного решения этой системы, который реализован в виде параллельной программы на языке Си по технологии CUDA с использованием графических ускорителей видеокарт. Проведены тестовые расчеты, демонстрирующие работу программы.

Работа выполнена при финансовой поддержке РФФИ (проекты №14-01-00130 и16-31-00078). Автор считает своим долгом выразить благодарность к.ф.-м.н. О.В. Садовской и д.ф.-м.н., профессору В.М. Садовскому за постановку задачи и обсуждение результатов.

Литература:

1. Ericksen J.L. Conservation laws for liquid crystals // Trans. Soc. Rheol. – 1961. – V. 5. P. 23–34.
2. Leslie F.M. Some constitutive equations for liquid crystals // Arch. Ration. Mech. Anal. – 1968. – V. 28. – P. 265–283.
3. Аэро Э.Л., Булыгин А.Н. Уравнения движения нематических жидких кристаллов // Прикл. матем. и механ. – 1971. – Т. 35, вып. 5. – С. 879–891.
4. Садовский В.М., Садовская О.В. Об акустическом приближении термомеханической модели жидкого кристалла // Физическая мезомеханика. – 2013. – Т. 16, № 3. – С. 55–62.
5. Sadovskii V.M. Equations of the dynamics of a liquid crystal under the influence of weak mechanical and thermal perturbations // AIP Conf. Proc. – 2014. – V. 1629. – P. 311–318.
6. Sadovskaya O.V. Numerical simulation of the dynamics of a liquid crystal in the case of plane strain using GPUs // AIP Conf. Proc. – 2014. – V. 1629. – P. 303–310.
7. Смолехо И.В. Параллельная реализация алгоритма для описания термоупругих волн в жидких кристаллах // Молодой ученый. Часть I. – 2015. № 11(96). – С. 107–112.