Жидкие кристаллы являются уникальными веществами благодаря необычному сочетанию анизотропных свойств, присущих кристаллам, и текучести, свойственной жидкостям. Жидкие кристаллы состоят из сложных органических молекул продолговатой формы. От обычных кристаллов они отличаются отсутствием жесткой кристаллической решетки. Общим свойством всех кристаллов является наличие порядка в пространственной ориентации молекул. В зависимости от порядка пространственной ориентации жидкие кристаллы делятся на три вида: нематические, смектические и холестерические. Подвижность молекул жидких кристаллов позволяет воздействием внешних сил изменять их ориентацию и таким образом управлять их свойствами. С помощью жидких кристаллов обнаруживают пары вредных химических соединений и опасные для здоровья человека гамма- и ультрафиолетовое излучения. На основе жидких кристаллов созданы измерители давления, детекторы ультразвука. Обширная область применения жидкокристаллических веществ – информационная техника: электронные часы, цветные телевизоры с жидкокристаллическим экраном и т.п. Физические свойства жидких кристаллов описаны, например, в [1, 2].
В данной работе рассматриваются нематические жидкие кристаллы, молекулы которых ориентированы в определенном направлении. Разработана параллельная программа для вычислительных систем на графических ускорителях, позволяющая исследовать численно математическую модель термомеханического поведения жидких кристаллов. В работе [3] построена упрощенная модель нематического жидкого кристалла как акустической микронеоднородной среды с вращающимися частицами. В [4, 5] представлено обобщение этой модели на случай вязкоупругих деформаций при произвольных по величине поворотах частиц.
Основная система уравнений модели жидкого кристалла в акустическом приближении в двумерном случае выглядит следующим образом (см. [3]):
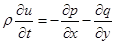 ,
, 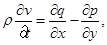
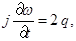
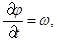
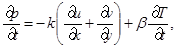
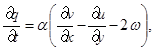 (1)
(1)
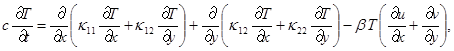
где u и v – компоненты вектора скорости; w – угловая скорость; 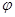 – угол поворота молекул кристалла; p – гидростатическое давление; q – касательное напряжение; T – абсолютная температура; r – плотность; j – момент инерции; k – модуль объемного сжатия; a – модуль упругого сопротивления вращению; b – коэффициент теплового расширения; c – удельная теплоемкость;
– угол поворота молекул кристалла; p – гидростатическое давление; q – касательное напряжение; T – абсолютная температура; r – плотность; j – момент инерции; k – модуль объемного сжатия; a – модуль упругого сопротивления вращению; b – коэффициент теплового расширения; c – удельная теплоемкость; 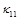 ,
, 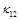 и
и 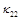 – компоненты тензора теплопроводности:
– компоненты тензора теплопроводности:
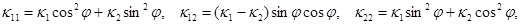
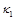 и
и 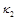 – коэффициенты теплопроводности в направлении ориентации молекул жидкого кристалла и в поперечном направлении; x, y и t – пространственные переменные и время. В систему (1) входят уравнения поступательного и вращательного движения, уравнение для угла поворота, уравнения состояния для давления и касательного напряжения, уравнение анизотропной теплопроводности с переменными коэффициентами.
– коэффициенты теплопроводности в направлении ориентации молекул жидкого кристалла и в поперечном направлении; x, y и t – пространственные переменные и время. В систему (1) входят уравнения поступательного и вращательного движения, уравнение для угла поворота, уравнения состояния для давления и касательного напряжения, уравнение анизотропной теплопроводности с переменными коэффициентами.
Численное решение краевых задач для системы (1) осуществляется с помощью метода двуциклического расщепления по пространственным переменным [6]. Рассматривается расчетная область в форме квадрата. Искомыми величинами являются скорости и напряжения, а также угловая скорость и температура внутри расчетной области.
В двумерном случае на каждом временном интервале 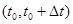 расщепление включает в себя 5 этапов: решение одномерных подсистем уравнений акустики жидкого кристалла и связанных уравнений теплопроводности в направлениях x и y на полуинтервале по времени
расщепление включает в себя 5 этапов: решение одномерных подсистем уравнений акустики жидкого кристалла и связанных уравнений теплопроводности в направлениях x и y на полуинтервале по времени 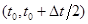 ; пересчет величин q, w и j по схеме Кранка-Николсон; повторный пересчет в направлениях y и x на втором полуинтервале
; пересчет величин q, w и j по схеме Кранка-Николсон; повторный пересчет в направлениях y и x на втором полуинтервале 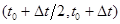 .
.
На этапах расщепления одномерные задачи решаются с использованием конечно-разностной схемы типа “предиктор–корректор” в следующей последовательности: сначала реализуется шаг “предиктор” для подсистемы уравнений акустики, затем решается уравнение теплопроводности, и в заключение выполняется шаг “корректор” матричной системы, правая часть которой зависит от температуры. Конечно-разностная схема, построенная по принципу схемы С.К. Годунова [7], применяется при решении акустических уравнений; схема Г.В. Иванова с контролируемой диссипацией энергии [8] – при решении уравнения теплопроводности. Температура в каждом направлении вычисляется с помощью трехточечной прогонки. Схема является неявной на шаге “предиктор” и явной на шаге “корректор”. Такая конструкция метода расщепления обеспечивает устойчивость численного решения в двумерном случае.
На 1-м и 5-м этапах метода расщепления считается, что искомое решение зависит только от x, и система уравнений (1) преобразуется к следующему виду:
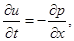
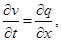
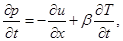
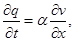
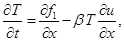
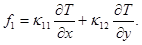
Аналогично на 2-м и 4-м этапах, когда решение зависит только от y, получим систему:
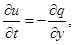
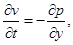
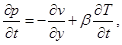
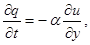
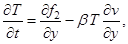
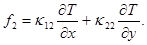
На 3-м этапе метода расщепления решается система уравнений:
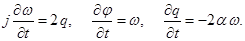
Таким образом, на этапах расщепления решаются уравнения акустики жидкого кристалла и уравнения теплопроводности.
Аппроксимируем уравнения этих систем на каждом временном слое заменой производных по времени и пространственным переменным конечными разностями. Для подсистемы уравнений акустики на шаге “предиктор” вычисляются следующие величины в направлении x:
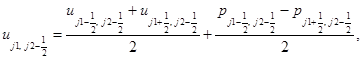
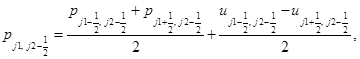 (2)
(2)
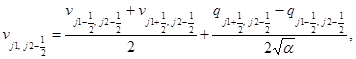
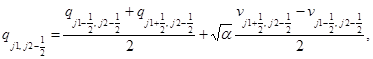
а в направлении у:
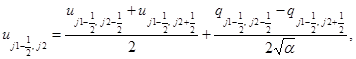
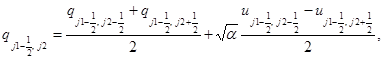 (3)
(3)
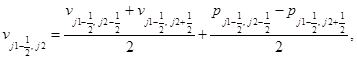

Соотношения шага “корректор” в направлении x:
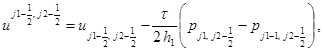
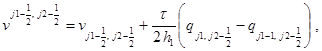 (4)
(4)
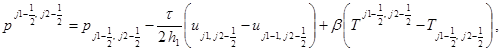
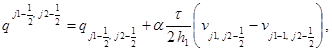
в направлении у:
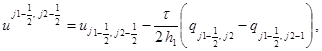
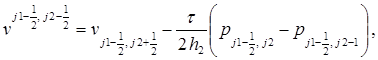 (5)
(5)
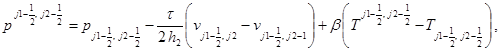
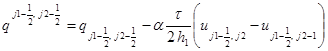 ,
,
(здесь 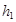 и
и 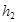 – шаги пространственной сетки в направлениях x и y,
– шаги пространственной сетки в направлениях x и y, 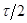 – полушаг по времени, верхние индексы относятся к следующему временному слою).
– полушаг по времени, верхние индексы относятся к следующему временному слою).
Схема Кранка-Николсон реализуется по следующим формулам:
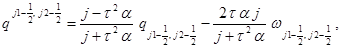
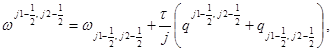 (6)
(6)
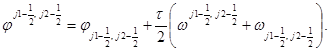
Уравнение анизотропной теплопроводности с переменными коэффициентами решается также с помощью схемы “предиктор-корректор”. На шаге “корректор” в каждом из направлений используются уравнения:
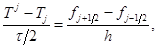
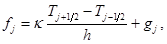 (7)
(7)
а на шаге “предиктор” – уравнения:
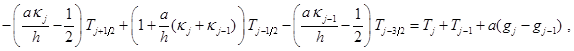 (8)
(8)
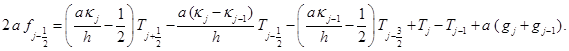 (9)
(9)
Вторые индексы здесь для краткости опущены; 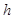 – шаг по пространству, в зависимости от направления в качестве
– шаг по пространству, в зависимости от направления в качестве 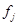 принимается
принимается 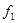 или
или 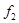 (это потоки, содержащие смешанные производные);
(это потоки, содержащие смешанные производные); 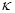 – коэффициент теплопроводности (
– коэффициент теплопроводности (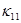 или
или 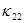 ); величины
); величины 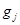 находятся по явной схеме через значения входящих в них переменных, взятых с предыдущего слоя по времени (сюда входят смешанные производные с коэффициентом
находятся по явной схеме через значения входящих в них переменных, взятых с предыдущего слоя по времени (сюда входят смешанные производные с коэффициентом 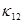 ). Температура в каждом направлении вычисляется с помощью метода трехточечной прогонки. Схема (7)–(9) является неявной на шаге “предиктор” и явной на шаге “корректор”. Условие устойчивости схемы:
). Температура в каждом направлении вычисляется с помощью метода трехточечной прогонки. Схема (7)–(9) является неявной на шаге “предиктор” и явной на шаге “корректор”. Условие устойчивости схемы: 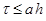 , где
, где 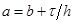 ,
, 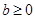 .
.
Описанный вычислительный алгоритм для решения системы уравнений (1) по формулам (2)–(9) реализован в виде параллельной программы для компьютеров с графическими ускорителями. Программа написана на языке Си с применением технологии CUDA (Compute Unified Device Architecture) для распараллеливания вычислений, позволяющей использовать графические ускорители видеокарт [9, 10]. Распараллеливание вычислений производится на этапах метода расщепления.
Для решения задач CUDA использует очень большое количество параллельных нитей, каждой из них соответствует один элемент вычисляемых данных. Фактически для каждого допустимого индекса входных массивов запускаем отдельную нить для осуществления нужных вычислений. Все они выполняются параллельно, и каждая может получить информацию о себе через встроенные переменные. Исходная задача разбивается на набор отдельных подзадач. Каждой подзадаче соответствует свой блок нитей.
На GPU (Graphical Processing Unit) расчетная область разбивается на квадратные блоки, содержащие одинаковое число нитей. Благодаря идентификаторам, имеющимся в CUDA, каждой нити ставится в соответствие ячейка разностной сетки. В параллельном режиме нити графического устройства выполняют однотипные операции в ячейках по расчету решения на шаге “предиктор” и после этого на шаге “корректор” схемы.
Верхний уровень иерархии в CUDA – сетка (grid) – соответствует всем нитям, выполняющим ядро. Следующий уровень – двумерный массив блоков (block). Каждый блок представляет собой двумерный массив нитей (thread). Все блоки, образующие сетку, имеют одинаковую размерность и размер. Каждый блок в сетке имеет свой адрес, состоящий из двух натуральных чисел. Также и каждая нить имеет двухзначный индекс. Так как одно и то же ядро выполняется одновременно с большим количеством нитей, для их определения используются встроенные переменные: threadIdx,blockIdx – двумерные целочисленные векторы; gridDim,blockDim – переменные, используемые для определения размеров сетки и блока.
В начале программы на CPU (Central Processing Unit) задаются размерности конечно-разностной сетки и все необходимые константы, описываются одномерные массивы и задаются начальные данные. Одновременно на GPU выделяется память под массивы для этих величин и всех необходимых вспомогательных величин. Затем необходимые константы и массивы копируются с CPU на GPU. На каждом шаге по времени последовательно реализуются этапы метода расщепления. На этапах расщепления графическим устройством выполняются все необходимые ядра (процедуры) в параллельном режиме. Для анализа результатов счета в контрольных точках по времени решение передается с GPU на CPU, и по полученным файлам данных рисуются линии уровня искомых величин графическими средствами персонального компьютера. После выполнения каждого из ядер производится барьерная синхронизация, чтобы обеспечить завершение вычислений каждой нитью до начала выполнения следующего ядра.
Проведена серия методических расчетов динамического деформирования жидких кристаллов при слабых механических и температурных воздействиях, демонстрирующих работу программы. На рис. 1 показаны результаты счета для задачи о действии трех P-образных и L-образных импульсов давления в нормальном направлении на части левой границы расчетной области в виде квадрата. Остальные части границы области считаются свободными от напряжений. Нагрузка действует некоторое время, а потом граница полностью освобождается от напряжений. Разностная сетка состоит из 1024´1024 ячеек.
Далее представлены численные результаты для задачи с заданной внутри всей расчетной области температурой 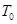 в начальный момент времени и нулевыми граничными условиями для всех величин. Расчеты проведены для разных коэффициентов теплопроводности:
в начальный момент времени и нулевыми граничными условиями для всех величин. Расчеты проведены для разных коэффициентов теплопроводности: 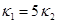 , угол поворота молекул жидкого кристалла j =
, угол поворота молекул жидкого кристалла j = 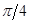 . На рис. 2 видно, что линии уровня температуры вытягиваются в направлении ориентации молекул.
. На рис. 2 видно, что линии уровня температуры вытягиваются в направлении ориентации молекул.
а) б)




Рис. 1. P-образные а) и L-образные б) импульсы давления на части левой границы:
линии уровня давления p (250 и 500-й шаги по времени – слева направо)



Рис. 2. Заданная начальная температура: линии уровня температуры T
(100, 200 и 500-й шаги по времени – слева направо)
Рис. 3 показывает, как распространяются волны давления и как они отражаются друг от друга.




Рис. 3. Заданная начальная температура: линии уровня давления p
(100, 200, 400 и 500-й шаги по времени – слева направо)
На рис. 4 представлены результаты расчетов для задачи о действии четырех источников тепла на нижней границе расчетной области (в нормальном направлении). Область действия каждого источника тепла – 10 см (при длине стороны квадрата 1 м). Видно, что линии уровня температуры ориентируются под заданным углом 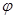 .
.
Расчеты выполнены на высокопроизводительном вычислительном сервере Flagman ИВМ СО РАН. Численно исследована эффективность работы программы. Проведено большое количество расчетов при разных размерностях сетки. Время счета параллельной программы сравнивалось со временем счета соответствующей последовательной программы. В расчетах зафиксировано ускорение работы параллельной программы примерно в 25 раз по сравнению с последовательной версией.
а) б)
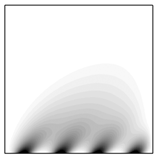
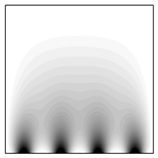
Рис. 4. Источники тепла на нижней границе: линии уровня температуры 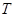 при коэффициентах теплопроводности
при коэффициентах теплопроводности 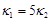 и углах поворота
и углах поворота 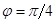 и
и 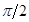
(1000-й шаг по времени)
Работа выполнена при финансовой поддержке РФФИ (код проекта 14-01-00130).
Литература:
1. Калугин А.Г. Механика анизотропных жидкостей. – М.: Изд-во Центра прикладных исследований при мех.-мат. ф-те МГУ, 2005. – 64 с.
2. Blinov L.M. Structure and Properties of Liquid Crystals. Heidelberg – New York – Dordrecht – London: Springer, 2011. – 439 p.
3. Садовский В.М., Садовская О.В. Об акустическом приближении термомеханической модели жидкого кристалла // Физическая мезомеханика, 2013. – Т. 16, № 3. – С. 55–62.
4. Sadovskii V.M. Equations of the dynamics of a liquid crystal under the influence of weak mechanical and thermal perturbations // AIP Conf. Proc, 2014. – V. 1629. – P. 311–318.
5. Sadovskaya O.V. Numerical simulation of the dynamics of a liquid crystal in the case of plane strain using GPUs // AIP Conf. Proc, 2014. – V. 1629. – P. 303–310.
6. Марчук Г.И. Методы расщепления. – М.: Наука, 1988. – 263 с.
7. Годунов С.К., Забродин А.В., Иванов М.Я., Крайко А.Н., Прокопов Г.П. Численное решение многомерных задач газовай динамики. – М.: Наука, 1976. – 400 с.
8. Иванов Г.В., Волчков Ю.М., Богульский И.О., Анисимов С.А., Кургузов В.Д. Численное решение динамических задач упругопластического деформирования твердых тел. – Новосибирск: Сиб. унив. изд-во, 2002. – 352 с.
9. Боресков А.В., Харламов А.А. Основы работы с технологией CUDA. – М.: ДМК Пресс, 2010. – 232 с.
10. Farber R. CUDA Application Design and Development. Amsterdam – Boston – Heidelberg – London – New York – Oxford – Paris – San Diego – San Francisco – Singapore – Sydney – Tokyo: Morgan Kaufmann / Elsevier, 2011. – 315 p.

