Нейросетевые технологии является мощным математическим аппаратом, что позволяет выявлять скрытые закономерности. Подобные задачи необходимо решать во многих предметных областях, таких как медицина, геологическая разведка, анализ сложных экономических систем и тому подобное. При этом, если в отдельных областях допустимо проводить обработку исходных данных в отложенном режиме, то во многих других, например, при диагностике актуального состояния технической системы, необходимо проводить анализ в режиме реального времени или в режиме, близком к нему.
К настоящему моменту времени применение нейросетевых технологий при работе с большими массивами данных во многом ограничивалось лабораторными исследованиями в режиме отложенного времени, поскольку программная реализация модели нейронной сети отличалась низкой скоростью работы или требовалась разработка специализированных аппаратных средств. Поэтому ставится задача — овладеть типичными современными аппаратными средствами и в полной мере задействовать их возможности для обеспечения существенного прироста производительности нейронной сети.
Реализация нейронной сети Кохонена сиспользованием технологии CUDA
Процесс обучения нейронной сети Кохонена можно представить в виде трех этапов: вычисление расстояния между представленным на сети образцом и каждым нейроном сети (рис. 1), определение победителя и изменение весовых коэффициентов. В самоорганизующихся картах Кохонена присутствует также дополнительный этап — определение мер соседства.
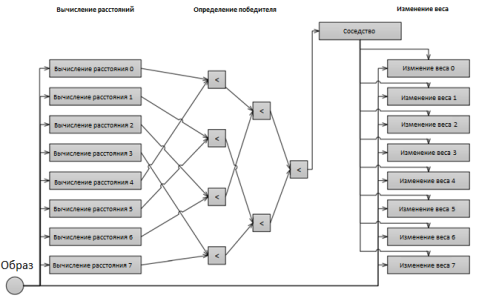
Рис. 1. Модель карты Кохонена, реализованной по технологии CUDA
Для нахождения расстояния может быть использована произвольная метрика. Если решаемая задача имеет географическую привязку или если осуществляется только предварительное ознакомление с предметной областью и ее свойства не выяснены, то часто используют евклидову метрику. Тогда расстояние определяется по формуле
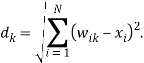
С целью повышения скорости обучения операцию извлечения квадратного корня можно исключить, так как в конечном итоге интерес представляет не собственно значение расстояния, а соотношение расстояний.
Рассмотрим модель показанную на рис. 1. Здесь в качестве примера показана сеть, состоящая из восьми нейронов, но общая ее структура при изменении количества нейронов существенно не изменится. Предполагается, что количество входных нейронов не задана условиями задачи и может быть выбрана произвольно. В этом случае она целесообразно задавать, учитывая оптимальное количество одновременно выполняемых потоков на графическом ядре. Использование меньшего количества нейронов приведет к тому, что графическое ядро будет загружено не полностью, следовательно, не будет достигнута максимально возможная производительность вычислительной системы. Увеличение числа нейронов реализуется довольно просто при условии, что их число является кратным количеству одновременно работающих потоков. В этом случае каждый элемент будет просчитывать два или более нейронов последовательно. Не рекомендуется использовать количество нейронов, некратное количеству потоков, поскольку, кроме простоя части процессорных элементов, это потребует добавления условных операторов, что в технологии CUDA является нежелательным, учитывая производительность.
Следующий этап — нахождение победителя. Для этого необходимо найти наименьшее расстояние и определить индекс соответствующего ему нейрона. Этот этап может быть представлен в виде задачи восхождения, то есть вычисления такого рода, когда на каждом шагу количество обрабатываемых данных уменьшается вдвое. Лучшим способом разбиения этого этапа на составляющие будет разделение массива исходных данных пополам и попарное сравнение между собой элементов, расположенных последовательно в каждой половине массива. Именно такой выбор элементов для сравнения связан с особенностями организации глобальной и общей памяти [3].
В случае работы с классической сетью Кохонена, обнаружив победителя, можно будет сказать, в какой именно из нейронов исходное значение должно равняться единице, а значит, можно сразу приступать к изменению весовых коэффициентов по формуле
![]()
где λ — коэффициент скорости обучения.
Этот процесс с вычислительной точки зрения выполняется аналогично этапу определения расстояний, то есть каждый элемент просчитывает вес одного нейрона, и эти расчеты выполняются параллельно.
Последовательность из этих трех этапов выполняется многократно. На каждой итерации на вход подается новый образец, который, как правило, избирается произвольно. Также общепринятой практикой является постепенное уменьшение коэффициента скорости обучения.
Несколько особняком стоит процесс определения мер соседства, который используется в самоорганизующихся картах. Его особенность заключается в том, что выполнить его можно единовременно перед началом обучения сети, поскольку соседство между нейронами не зависит от их весовых коэффициентов, а определяется исключительно, учитывая индексы нейронов и выбранный тип координатной сетки — прямоугольной или гексагональной. [5] Из-за сравнительно малого количества нейронов предварительное вычисление мер соседства вполне целесообразно, потому таблицу соседства можно хранить в общей памяти. При увеличении количества нейронов объема общей памяти может оказаться недостаточно. Задействовать для таблицы соседства глобальную память нет смысла, поскольку доступ к ней является одним из «узких» мест в архитектуре CUDA. Поэтому в последнем случае продуктивным решением будет выполнение расчета соседства между каждым из нейронов и нейроном заново на каждой итерации.
Анализ производительности
Для тестирования были использованы самоорганизующиеся карты Кохонена размером 16х16, 16х32 и 32х32. Они содержали три входных сигнала и один выходной. В этом случае смысловое наполнение сигналов значения не имеет. То есть это могут быть сигналы от датчиков температуры, давления, вибрации и т. д. Законы распределения значений в сигналах, частота их изменений, взаимная корреляция и другие показатели непосредственно на скорость обучения сети не влияют, однако они могут предоставить косвенное влияние, так как по меньшей зашумленности и из-за менее сложного закона взаимосвязи входных сигналов для обнаружения скрытых закономерностей достаточно будет меньшего количества итераций во время учебы.
На рис. 2 показана самоорганизующаяся карта на разных стадиях обучения. Начальный ее состояние (рис. 2, а) представляет собой полностью зашумленных область, поскольку начальные веса нейронов, как правило, назначаются случайно. На протяжении обучения карты на ней постепенно вырисовываются большие темные и светлые пятна, поскольку нейроны с близкими весами стремятся приблизиться друг к другу (рис. 2, б), а затем границы областей становятся четче выраженными, и часто при этом можно наблюдать несколько кластеров (рис. 2, в). В продолжение обучения кластеры становятся все более мелкими вплоть до отдельных нейронов (рис. 2, г). Такое положение, как правило, свидетельствует об определенном переобучении сети.

Рис. 2. Этапы обучения карты Кохонена: а — исходное состояние; б — 10 тыс. итераций, в — 200 тыс. итераций, г — 1 млн. итераций
Результат тестирования изображен на рис. 3. В этом случае фиксировалось количество учебных итераций, а именно — устанавливалось равным 1 млн. И оценивалось время, необходимое для их выполнения. Как видим, во всех случаях время не превысило 100 с. Подобное количество итераций во многих случаях будет больше, чем нужно для предварительной настройки сети, а полученное время обучения — вполне приемлемым для интерактивной работы оператора с вычислительной системой.
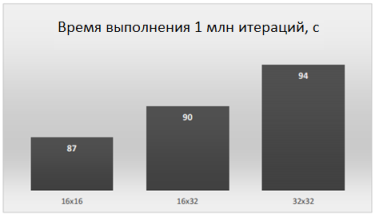
Рис. 3. Продуктивность карты Кохонена, реализованной при использовании технологии CUDA
Также видим, что при уменьшении размера самоорганизующейся карты время обучения снижается незначительно. Например, при переходе от карты размером 32x32 к карте размером 16x16, то есть за уменьшение количества нейронов в 4 раза, время обучения снизился примерно на 7 %. Такое поведение нейронной сети, реализованной в соответствии с моделью на рис. 2, согласуется с предсказуемой, поскольку одновременно со снижением количества нейронов уменьшалось и количество работающих потоков в GPU.
Размер обучающей выборки в проведенном тестировании равен 65 536. Ключевым здесь является то, что такой объем данных уже не может быть размещен в общей памяти, следовательно, предполагается, что массив образцов обучающей выборки размещен в глобальной памяти видеокарты. Учитывая числовые характеристики современных видеокарт и средние объемы выборок в большинстве задач, эту ситуацию можно считать характерной. При увеличении объема обучающей выборки может осуществляться подкачка данных из ОЗУ (при необходимости) в память видеокарты непосредственно в процессе вычислений на GPU. Существенного влияния на производительность не будет.
Выводы. На этапе разработки модели самоорганизующейся карты и при выборе ее количественных показателей, таких как количество нейронов и количество элементов в обучающей выборке, должно быть учтено много ограничений и особенностей GPU. В этом случае реализация самоорганизующейся карты Кохонена с использованием графического процессора на основе технологии CUDA позволяет достичь скорости обучения сети около 105 итераций в секунду, что открывает перспективы использования самоорганизующихся карт в системах мягкого реального времени.
Литература:
- Кохонен Т. Самоорганизующиеся карты // пер. с англ В. Агеев; под ред. Ю. Тюменцева. — М.: Бином, 2008. — 656 с.
- Гергель В. П. Теория и практика параллельных вычислений. — М.: Бином. Лаборатория знаний, 2007. — 424 с.
- Олещук О. В., Попель А. Е., Копытчук М. Б. Моделирование полносвязной нейронной сети с использованием технологии CUDA// Вестник Национального университета «Львовская политехника». — 2012. — № 747. — С. 131–139.
- CUDA Zone. http://www.nvidia.ru/object/cuda_home_new_ru.html (Last access: 01.12.2016).
- Юндин А. С. Использование нейронных сетей для повышения надежности хранения данных // Молодой ученый. — 2016. — № 27.

