Анализ физических явлений в радиотехнических цепях с использованием теории «парных эхо»



Теория «парных эхо» [1] является эффективным математическим аппаратом для аналитического моделирования различного рода физических явлений, которые происходят в радиотехнических цепях и каналах связи. Радиотехнические цепи могут быть как линейными, так и нелинейными. И в том, и в другом случае теория «парных эхо» позволяет анализировать происходящие в них физические явления.

Самым простым оператором, который приводит к появлению на выходе функционального преобразователя пары слагаемых симметричных относительно определенной точки на оси абсцисс, является перемножение функций.

Перемножим, например, косинусоидальные функции:

y = Аcosx₁·Bcosx₂ = 0.5AB [cos(x₁+x₂)+cos(x₁-x₂)].

Здесь слагаемые на оси абсцисс располагаются симметрично относительно значений х₁ при х₁≥x₂ или симметрично относительно x₂ при x₂≥х₁.

Аналогично:

y = Аsinx₁·Bsinx₂ = 0.5AB [cos(x₁+x₂)-cos(x₁-x₂)].

y = Аsinx₁·Bcosx₂ = 0.5AB [sin(x₁-x₂)+sin(x₁+x₂)].

y = Аcosx₁·Bsinx₂ = 0.5AB [sin(x₁+x₂)-sin(x₁-x₂)].

Известно также, что функциональное преобразование вида cos(Аcosx) приводит к появлению суммы слагаемых, которые располагаются зеркально относительно значения аргумента, равного 0 [2, 3]:

,

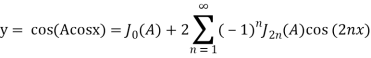где J_n(A) — функция Бесселя 1-го рода от действительного аргумента, графики которых приведены на рисунке 1.

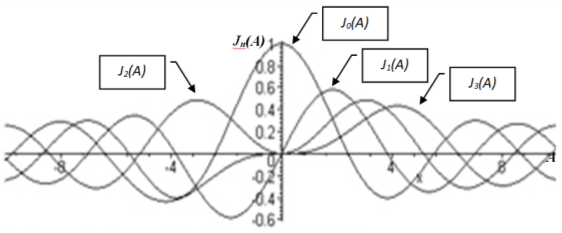
Рис. 1. Функции Бесселя 1-го рода от действительного аргумента

Аналогично:

;

;

.

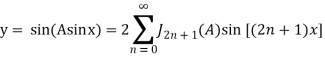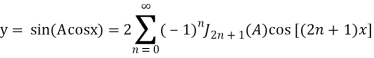Известно также функциональное преобразование вида , которое представляет собой сумму слагаемых, расположенных зеркально относительно начала координат [3]:

;

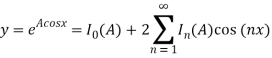И аналогично:

y=.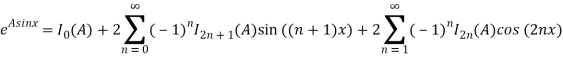

где I_n(A) — функция Бесселя 1-го рода от мнимого аргумента, графики которых приведены на рисунке 2.

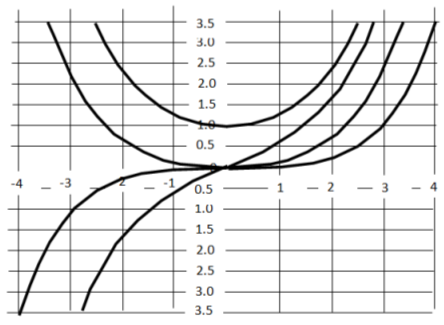
Рис. 2. Функции Бесселя 1-го рода от мнимого аргумента

С помощью вышеописанного математического аппарата можно анализировать различные явления в радиотехнических цепях и каналах связи:

– модуляцию сигналов;

– линейные искажения в каналах связи;

– нелинейные искажения в радиотехнических цепях.

Рассмотрим некоторые примеры использования теории «парных эхо» для анализа отдельных физических явлений в радиотехнических цепях.

Амплитудная модуляция

При амплитудной модуляции (АМ) в соответствии с законом передаваемого сообщения меняется амплитуда модулируемого сигнала. При однотональной АМ модулирующий сигнал представляет собой гармоническое колебание и модулированное колебание можно записать в виде:

+0.5m,

где U₀ — амплитуда модулируемого (несущего) колебания;

m — коэффициент амплитудной модуляции;

𝛀 — частота модулирующего колебания;

ω₀ — частота несущего колебания.

‎‎ ω₀>> 𝛀.

Согласно выше полученному выражению спектр амплитудно-модулированного гармоническим сигналом несущего колебания состоит из трех составляющих, частота одной из них равна частоте несущего колебания, а две другие отстоят от нее симметрично справа (верхняя боковая составляющая) и слева (нижняя боковая составляющая) на расстоянии, равном частоте модулирущего колебания. На рисунке 3 изображены осциллограмма и спектрограмма АМ колебания с коэффициентом модуляции m=1.

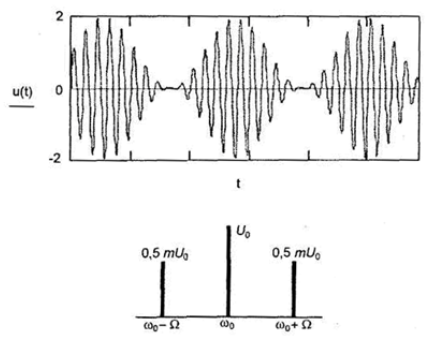
Рис. 3. Осциллограмма и спектрограмма АМ колебания с коэффициентом модуляции m=1

Частотная модуляция

При частотной модуляции (ЧМ) в соответствии с законом передаваемого сообщения меняется частота модулируемого гармонического сигнала. При однотональной ЧМ модулирующий сигнал представляет собой гармоническое колебание и модулированное колебание можно записать в виде:

=

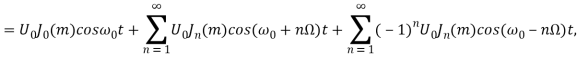
где U₀ — амплитуда модулируемого (несущего) колебания;

m — индекс угловой модуляции;

𝛀 — частота модулирующего колебания;

ω₀ — частота несущего колебания.

ω₀>> 𝛀.

Согласно выше полученному выражению спектр частотно-модулированного гармоническим сигналом несущего колебания состоит теоретически из бесконечно большого числа составляющих, частота одной из них равна частоте несущего колебания, а остальные отстоят от нее симметрично справа и слева на расстояниях, кратных частоте модулирующего колебания. На рисунке 4 изображены осциллограммы несущего колебания (а), модулирующего колебания (б) и модулированного колебания (в), а также спектрограмма ЧМ колебания (с).

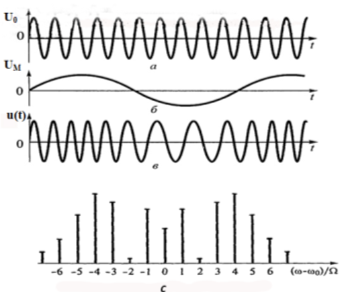
Рис. 4. Осциллограммы несущего колебания (а), модулирующего колебания (б), модулированного колебания (в) и спектрограмма ЧМ колебания (с)

Канал связи скосинусоидальными искажениями амплитудно-частотной характеристики

Рассмотрим канал связи с неограниченной полосой пропускания частот, с косинусоидальными искажениями амплитудно-частотной (АЧХ) K(ω) и с линейной (без искажений) фазо-частотной (ФЧХ) φ(ω)=Тω характеристиками.

Амплитудно-частотная характеристика (АЧХ) с косинусоидальными искажениями описывается выражением:

.

Здесь K₀ — коэффициент передачи канала связи при отсутствии искажений;

k — амплитуда искажающей АЧХ косинусоиды (глубина искажений), ;

Определим импульсную характеристику канала связи g(t) путем обратного преобразования Фурье от передаточной функции

где Т — время группового запаздывания в канале связи, обусловленное его фазо-частотной характеристикой.

.

На рисунке 5(а) и 5(b) изображены, соответственно АЧХ и ФЧХ такого канала связи:

a — АЧХ канала связи с косинусоидальными искажениями$

b — ФЧХ канала связи без искажений.

Известно [5], что

С учетом этого:

Из полученного равенства следует, что косинусоидальные искажения АЧХ канала связи приводят к появлению дополнительных двух «эхо-сигналов». Второе слагаемое последней строки равенства соответствует основному сигналу на выходе канала связи, запаздывающему относительно поступающего на вход канала связи сигнала на время T, которое является средней крутизной фазо-частотной характеристики этого канала связи. Первое слагаемое соответствует сигналу, опережающему основной сигнал на время , а последнее слагаемое — сигналу, отстающему от основного сигнала на время . При этом уровни опережающего и отстающего сигналов зависят от амплитуды искажающей АЧХ косинусоиды k.

Рассмотренный случай соответствует трех-лучевому каналу связи с постоянными параметрами. На рисунке 5(с) приведена выходная реакция канала связи с косинусоидальными искажениями АЧХ на единичное импульсное входное воздействие с амплитудой А.

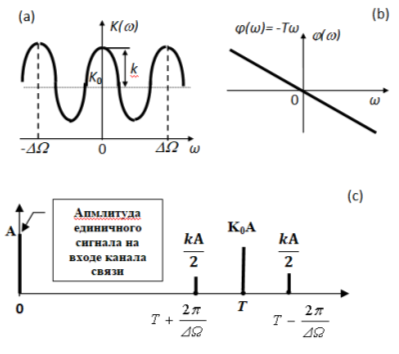
Рис. 5. Частотные характеристики канала связи с косинусоидальными (a) искажениями АЧХ и его импульсная характеристика (c)

Канал связи ссинусоидальными искажениями фазо-частотной характеристики

Рассмотрим канал связи с неограниченной полосой пропускания частот, с равномерной (без искажений) АЧХ K₀(ω) и с синусоидальными искажениями ФЧХ φ(ω), как показано на рисунках 6(а) и 6 (b), соответственно.

На рисунке 6 (b) обозначено:

ΔФ — амплитуда отклонения ФЧХ от среднего значения Tω;

 — период искажающей ФЧХ синусоидальной функции.

Изображенная на рисунке 6 (b)ФЧХ описывается выражением:

Определим импульсную характеристику g(t) четырехполюсника с передаточной функцией вида:

Возьмем обратное преобразование Фурье от передаточной функции K(j):

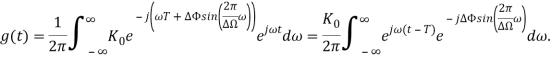
Выше было показано, что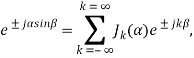

где J_k() — функции Бесселя 1-го рода, k-го порядка от действительного аргумента.

Следует учитывать тот факт, что J_k(-x)=(-1)^k J_k(x). То есть функции Бесселя нечетного порядка являются нечетными функциями, а функции Бесселя четного порядка являются четными функциями.

С учетом вышеизложенного можно записать:

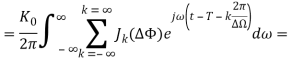
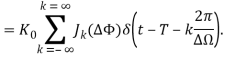
Из полученного равенства следует, что синусоидальные искажения ФЧХ канала связи приводят к появлению бесконечного числа дополнительных компонентов, которые по форме не отличаются от основного сигнала, но по времени опережают и отстают от него. Необходимо заметить, что при определенном значении амплитуды искажающей ФЧХ синусоиды уровни отдельных дополнительных сигналов по порядковому номеру n от основного (нулевого) сигнала могут принимать значение равное нулю, когда соответствующие им функции Бесселя J_n(ΔФ) = 0. Время отставания и время опережения всех дополнительных сигналов относительно основного кратно значению 2π/ΔΩ. На рисунке 6(с) изображена реакция на единичный импульс канала связи с синусоидальными искажениями ФЧХ.

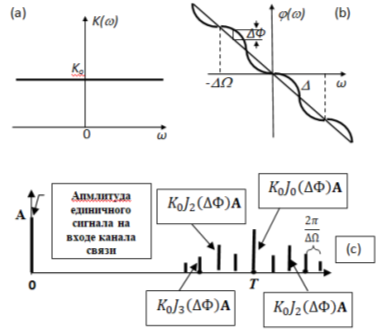
Рис. 6. Частотные характеристики канала связи с синусоидальными (b) искажениями ФЧХ и его импульсная характеристика (c)

Спектральный состав тока, протекающего через полупроводниковый диод при приложенном кнему гармоническом напряжении

Основное выражение для зависимости тока через p-n переход полупроводникового диода от приложенного к нему напряжения описывается выражением [6]:

,

α=q/kT,

где - ток насыщения диода,

q — заряд электрона,

k — постоянная Больцмана,

Т — абсолютная температура.

Соответствующая вольт-амперная характеристика диода изображена на рисунке 7(а).

Рассмотрим вариант воздействия на диод гармонического напряжения:

U(t)=U₀cosω₀t.

В этом случае ток через диод будет описываться выражением:

.

Из этого выражения видно, что ток диода при воздействии на него гармонического напряжения представляет собой сумму постоянной составляющей и бесконечно большого числа гармоник с частотами кратными частоте воздействующего на диод напряжения, которые симметрично расположены относительно постоянной составляющей вдоль оси частот как в сторону положительных, так и в сторону отрицательных значений частоты. Этот спектр представлен на рисунке 7(b).

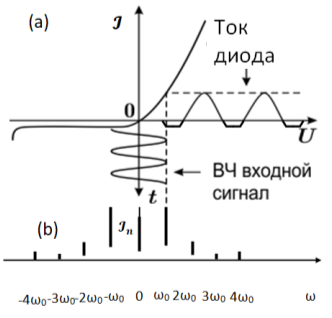
Рис. 7. Вольт-амперная характеристика полупроводникового диода (а) и спектрограмма тока диода (b) при приложенном к нему гармоническом напряжении

Анализ нелинейных явлений вусилительных каскадах

Рассмотрим наиболее характерный для нелинейных радиотехнических цепей случай активного усилительного каскадща, проходная характеристика которого u_вых(u_вх) обозначена на рисунке 8(а) сплошной жирной линией.

Произведем аппроксимацию проходной характеристики усилителя двухпараметрической функцией [7]:

Из рисунка 8 видно, что для уровней колебания u_вх, не превосходящих значения Δu, аппроксимирующая проходную характеристику кривая соответствует типичной проходной характеристике усилительного каскада. При этом очевидно, что при u_вх = Δu имеет место достаточно глубокое ограничение выходного колебания u_вых. Если же уровень колебания u_вх превосходит значение Δu, то передаточная характеристика начинает заметно отклоняться от уровня ограничения, и адекватность данной математической модели нарушается. В этом случае следует считать усилительный каскад вышедшим из строя по причине поступления на его вход напряжения выше допустимого уровня.

Рис. 8. Проходная характеристика усилителя (а) и спектр сигнала на выходе усилителя при гармоническом входном воздействии (b)

Пусть на вход усилителя подается гармоническое колебание с начальным смещением U₀:

.

С учетом выше приведенных формул получим выражение для напряжения на выходе усилителя при моногармоническом входном воздействии:

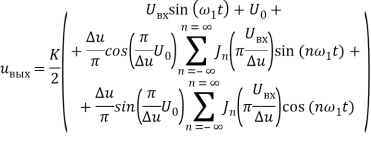
Из этого выражения следует, что при моногармоническом воздействии на вход усилителя с нелинейной передаточной характеристикой на его выходе присутствует бесконечно большое количество гармоник, расположенных симметрично относительно нуля на оси частот («парные эхо»), как это изображено на рисунке 8(b). При этом, если начальное смещение будет равно нулю (нечетная передаточная характеристика), то с учетом того, что J_-n(x)=(-1)ⁿJ(x) будут присутствовать только нечетные гармоники. Если начальное смещение равно Δu/2, то на выходе усилителя будут присутствовать только четные гармоники.

Из этого же выражения следует, что амплитудная характеристика усилителя описывается формулой:

.

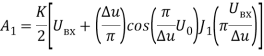На рисунке 9 приведено семейство амплитудных характеристик нелинейного усилителя для различных значений начального смещения U₀.

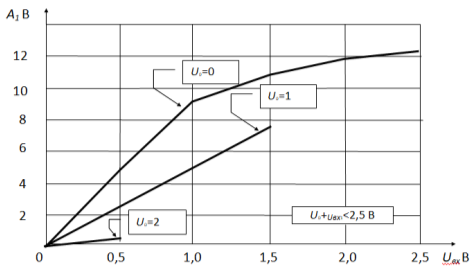
Рис. 9.семейство амплитудных характеристик нелинейного усилителя для различных значений начального смещения U₀

Заключение

Таким образом, и при модуляции сигналов, и при линейных искажениях в каналах связи, и при нелинейных искажениях в активных элементах трактов радиоаппаратуры анализ физических явлений возможно производить с использованием единого математического аппарата, который получил условное название теории «парных эхо» включающей в себя как элементарные правила перемножения гармонических сигналов, так и более сложную теорию разложения функций в ряды Фурье, у которых коэффициентами являются функции Бесселя первого рода.

Литература:

1. Кук Ч., Бернфельд М. Радиолокационные сигналы. Перевод с английского под реакцией В. С. Кельзона. –М.: Советское радио, 1971, — 568 с.
2. Корнеев Б. Г. Введение в теорию бесселевых функций. -М.: Наука, 1971. — 287 с.
3. Справочник по специальным функциям. Под ред. Абрамовица М. и Стиган И. Пер. с англ. — М.: Наука, 1979. 832 с.
4. Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений. -М.: Наука, 1971. — 1008 с.
5. Баскаков С. И. Радиотехнические цепи сигналы. Изд. 4, испр. и доп. М.: Радиотехника, 2016. 528 с.
6. Специальный физический практикум, ч. 2. Под ред. А. А. Харламова. — М.: МГУ, 1977. 376 с.
7. Хазан В. Л. Каналы связи. — Изд-во Palmarium Academic Publishing, 2015. — 230 c.