В статье изложена работа по созданию размерной типологии для промышленного производства формы для студенток СППО. Она начинается с выбора размерных признаков, необходимых для конструирования, разработки программы и методики измерений.
Для построения размерной типологии весь полученный антропометрический материал подвергают математической обработке.
Для каждого из признаков в результате математической обработки находят такие значения (статистические параметры), которые характеризуют величину и вариабельность признака в выборке, а соответственно и в генеральной совокупности.
Для получения достоверных данных обработка антропометрического материала должна рассматриваться как самостоятельная задача и проводиться так же, как сбор материала, по определенной методике, основанной на методах математической статистики.
Математическая статистика — наука, которая изучает вопросы соотношения генеральной совокупности и выборок. Еще в конце XIX века ветвь математической статистики, которая занимается применением математических методов для изучения разнообразия живых существ, в том числе и человека, получила название биометрии [1].
Как бы однородна ни была изучаемая группа людей, любой из антропометрических признаков внутри этой группы обнаруживает большую или меньшую изменчивость. Если измерена определенная группа людей, то можно заранее сказать, что различные значения любого из антропометрических признаков в этой группе встречаются с разной частотой.
Для получения характеристики вариабельности антропометрических признаков обратимся к конкретному материалу.
Допустим, что нужно проанализировать измерения длины тела у группы женщин, состоящей из 30 человек. Сначала эти данные представляют в виде упорядоченной таблицы, где их располагают в порядке возрастания (табл. 1.1). Далее следует найти наибольшее и наименьшее значения признака в группе. Минимальным значением длины тела в данной группе будет 150, а максимальным — 170 см.
Для удобства дальнейших вычислений отдельные значения признака группируют в классы. Число классов должно быть 15–15, так как при меньшем их числе снижается точность расчета. В том случае, если в выборке число наблюдений менее 60, значения признака не группируют в классы.
Интервал между двумя соседними классами — классовый интервал — определяют по формуле [1]
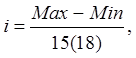
где Max — наибольшее значение признака в выборке;
Min — наименьшее значение признака в выборке.
Разность между наибольшим и наименьшим значениями признака в выборке (Max — Min) называется размахом вариабельности признака в выборке. При получении дробной величины i ее округляют до 0,5 или до целого числа.
В нашем примере (см. табл. 1):
1. Рост
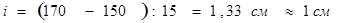
2. Обхват груди
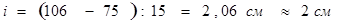
3. Обхват талии
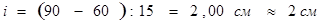
Это значит, что в один класс следует объединить значения длины тела, которые отличаются друг от друга не более чем на 1 см. Таким образом, вместо 60 отдельных значений можно записать 15 классов, в которые войдут все значения данного признака.
Далее определяют границы классов, т. е. начальное (нижнее) и конечное (верхнее) значения каждого класса. За начальное значение класса удобно взять целое число или число, оканчивающееся на 0,5. Границы классов определяют так, чтобы не возникло сомнений, к какому классу относится то или иное значение.
Ниже приведены результаты измерений по выбранным в программе измерениям.
Таблица 1.1
Значения длины тела (Р), см (женщины 17–19 лет, г. Бухара, 2014 г.)
|
150 151 152 153 153 153 154 154 155 155 |
155 156 156 156 157 157 157 157 157 158 |
158 158 158 159 159 159 159 160 160 160 |
160 160 160 161 161 162 162 163 163 163 |
164 164 164 165 165 165 166 166 167 167 |
167 167 168 168 168 169 169 169 170 170 |
Таблица 1.2
Значения обхват груди 3 (Ог3), см (женщины 17–19 лет, г. Бухара, 2014 г.)
|
75 75 76 76 77 77 77 78 78 79 |
80 80 81 81 81 82 82 82 83 83 |
83 84 84 85 85 86 86 86 87 87 |
87 87 88 88 88 88 88 88 89 89 |
89 89 90 90 90 91 91 91 92 92 |
92 93 94 95 96 98 100 102 104 106 |
Таблица 1.3
Значения обхват талии (От), см (женщины 17–19 лет, г. Бухара, 2014 г.)
|
60 60 60 61 61 62 62 63 63 63 |
64 64 64 64 65 65 65 66 66 67 |
67 67 68 68 68 68 69 69 69 69 |
70 70 70 71 71 72 72 72 73 73 |
74 74 74 75 75 76 76 76 77 77 |
78 78 79 80 82 84 84 86 88 90 |
После этого составляют таблицу, где в первую графу по вертикали записывают границы классов, во вторую графу — численность значений в каждом классе (табл.2).
Таблица 2.1
Вариационный ряд длин тела (женщины 17–19 лет, г. Бухара, 2014 г.)
|
Границы классовых интервалов, см |
Число значений в каждом классе, ед. |
Границы классовых интервалов, см |
Число значений в каждом классе, ед. |
|
150–150,9 151–151,9 152–152,9 153–153,9 154–154,9 155–155,9 156–156,9 157–157,9 158–158,9 159–159,9 160–160,9 |
1 1 1 2 2 3 3 5 4 4 6 |
161–161,9 162–162,9 163–163,9 164–164,9 165–165,9 166–166,9 167–167,9 168–168,9 169–169,9 170–170,9 |
2 2 3 3 3 2 4 4 3 2 |
|
n= 60 |
Таблица 2.2
Вариационный ряд по обхват груди 3 (женщины 17–19 лет, г. Бухара, 2014 г.)
|
Границы классовых интервалов, см |
Число значений в каждом классе, ед. |
Границы классовых интервалов, см |
Число значений в каждом классе, ед. |
|
75–76,9 77–78,9 79–80,9 81–82,9 83–84,9 85–86,9 87–88,9 89–90,9 |
4 5 3 6 5 5 10 7 |
91–92,9 93–94,9 95–96,9 97–98,9 99–100,9 101–102,9 103–104,9 105–106,9 |
6 2 2 1 1 1 1 1 |
|
n= 60 |
Таблица 2.3
Вариационный ряд по обхват талии (женщины 17–19 лет, г. Бухара, 2014 г.)
|
Границы классовых интервалов, см |
Число значений в каждом классе, ед. |
Границы классовых интервалов, см |
Число значений в каждом классе, ед. |
|
60–61,9 62–63,9 64–65,9 66–67,9 68–69,9 70–71,9 72–73,9 74–75,9 |
5 5 7 5 8 5 5 5 |
76–77,9 78–79,9 80–81,9 82–83,9 84–85,9 86–87,9 88–89,9 90–91,9 |
5 3 1 1 2 1 1 1 |
|
n= 60 |
При большом числе классов (т. е. при малом классовом интервале) кривая будет иметь зигзагообразную форму, при малом числе классов (при большом классовом интервале) будет дана неполная характеристика вариационного ряда. Поэтому нужное число классов при построении кривой распределения определяется исходя из численности выборки (табл.3) [1].
Таблица 3
Определение числа классов при заданной численности выборки для построения вариационной кривой
|
Число случаев п |
Число классов L |
Число случаев п |
Число классов L |
|
Меньше 50 50–100 100–190 190–400 |
6 7 8 9 |
400–730 730–1460 1460–3030 3030–5880 |
10 11 12 13 |
Определив число классов для заданной численности выборки, находят классовый интервал
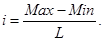
Полученное значение интервала следует округлять.
Так, для рассматриваемого примера (см. табл. 1) численность выборки п=30; число классов для данной численности по табл. 3 равно 7.
Минимальное значение длины тела в выборке равно 150, максимальное — 170 см; следовательно, классовый интервал для построения вариационной кривой распределения
i = (170,9–150)/7= 2,98 см = 3 см.
Минимальное значение обхват груди 3 в выборке равно 75, максимальное — 106,9 см; следовательно, классовый интервал для построения вариационной кривой распределения
i = (106,9–75)/7= 4,6 см = 5 см.
Минимальное значение обхват талии в выборке равно 60, максимальное — 91,9 см; следовательно, классовый интервал для построения вариационной кривой распределения
i = (91,9– 60)/7= 4,6 см = 5 см.
Полученный классовый интервал в полтора раза больше, чем при построении вариационного ряда в табл. 2.
Объединение значений признака в классы для построения вариационной кривой проводится по определенному правилу.
Для нашего примера нижней границей первого класса будет значение 150 см, а верхней границей класса — 152,9 см; второй класс будет включать значения от 153,0 до 155,9 см и так далее до 168,0–170,9 см (табл. 4.1.).
Таблица 4.1
Вариационный ряд длин тела для построения кривой распределения (женщины 17–19 лет, г. Бухара, 2014 г.)
|
Границы классовых интервалов, см |
Число значений в каждом классе, ед. |
Границы классовых интервалов, см |
Число значений в каждом классе, ед. |
|
150,0–152,9 153,0–155,9 156,0–158,9 159,0–161,9 |
3 8 12 12 |
162,0–164,9 165,0–167,9 168,0–170,9
|
8 9 8 |
|
n = 60 |
Таблица 4.2
Вариационный ряд обхват груди 3 для построения кривой распределения (женщины 17–19 лет, г. Бухара, 2014 г.)
|
Границы классовых интервалов, см |
Число значений в каждом классе, ед. |
Границы классовых интервалов, см |
Число значений в каждом классе, ед. |
|
75–79,9 80–84,9 85–89,9 90–94,5 |
10 13 19 11 |
95–99,9 100–104,9 105–109,9 |
3 3 1 |
|
n = 60 |
Таблица 4.3
Вариационный ряд обхват талии для построения кривой распределения (женщины 17–19 лет, г. Бухара, 2014 г.)
|
Границы классовых интервалов, см |
Число значений в каждом классе, ед. |
Границы классовых интервалов, см |
Число значений в каждом классе, ед. |
|
60–64,9 65–69,9 70–74,9 75–79,9 |
14 16 13 10 |
80–84,9 85–89,9 90–94,9 |
4 2 1 |
|
n = 60 |
Всякий вариационный ряд можно изобразить графически. На графике вариационный ряд изображается вариационной кривой (кривой распределения).
При построении кривой распределения величину классового интервала определяют не таким способом, как при составлении вариационного ряда.
При построении кривой распределения на графике по оси абсцисс х откладывают средние значения каждого класса, которые равны сумме значений нижней и верхней границ каждого класса, деленной на два.
1. Длина тела. Так, среднее значение для первого класса будет (150,0 + 152,9)/2 = 151,45см (≈151,5), для второго класса — 154,45 см (≈154,5) и т. д.
|
|
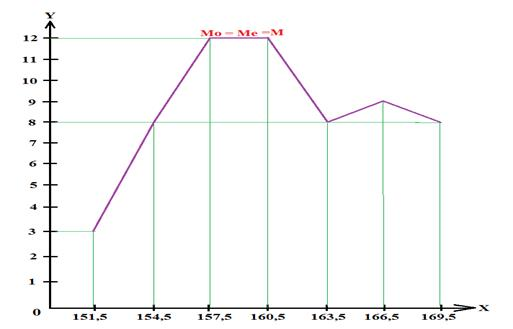
Рис. 1. Вариационная кривая по длин тела (женщины 17–20 лет)
2. Обхват груди 1.2. Так, среднее значение для первого класса будет (75,0 + 79,9)/2 = 77,45см(≈77,5), для второго класса — 82,45(≈82,5) см и т. д.
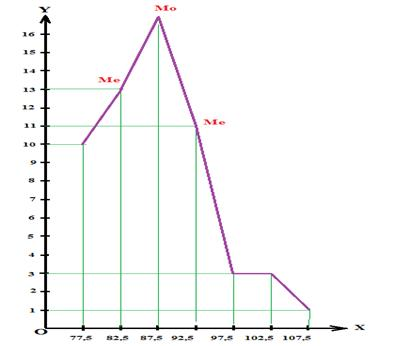
Рис. 2. Вариационная кривая по обхват груди 3 тела (женщины 17–20 лет)
3. Обхват талии. Так, среднее значение для первого класса будет (60,0 + 64,9)/2 = 62,45см(≈62,5), для второго класса — 67,45(≈67,5) см и т. д.
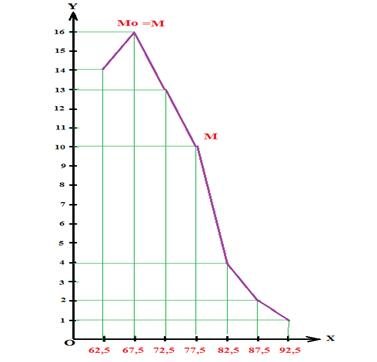
Рис. 3. Вариационная кривая по обхват талии тела (женщины 17–20 лет)
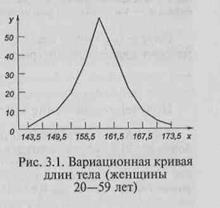
На оси ординат у откладывают частоту встречаемости признака. Кривая распределения (вариационная кривая) длины тела для данного примера изображена на рис. 1.
Анализируя форму вариационной кривой (или распределение численностей в вариационном ряду), можно обнаружить, что максимальная высота кривой (т. е. наибольшая численность) приходится на класс, который лежит посередине ряда. Вправо и влево от класса с максимальной численностью на кривой распределения (или вверх и вниз от этого класса в табл. 4) число значений признака в каждом классе постепенно убывает, имея наименьшие значения в первом и последнем классах. Подобная закономерность в вариабельности значений признака в вариационном ряду наблюдается у всех антропометрических признаков. [2].
В данной статье подробно описано построение программы измерений, были проведены антропометрические измерения телосложения девушек студентов колледжа. Были построены вариационного ряды и диаграммы кривых определяющих изменения параметров телосложения.
Литература:
1. Дунаевская Т. Н. и др. Размерная типология населения с основами анатомии и морфологии человека/Дунаевская Т. Н., Коблякова Е. Б., Ивлева Г. С. М., 1980.
2. Проблемы размерной антропологической стандартизации для конструирования одежды/Куршакова Ю. С. Дунаевская Т. Н., Зенкевич П. И. и др. М., 1978.