Применение методов динамики к расчету строительных конструкций
Авторы: Каверина Эвелина Витальевна, Татаркина Евгения Андреевна
Рубрика: 9. Педагогика высшей профессиональной школы
Опубликовано в
VI международная научная конференция «Педагогическое мастерство» (Москва, июнь 2015)
Дата публикации: 25.05.2015
Статья просмотрена: 504 раза
Библиографическое описание:
Каверина, Э. В. Применение методов динамики к расчету строительных конструкций / Э. В. Каверина, Е. А. Татаркина. — Текст : непосредственный // Педагогическое мастерство : материалы VI Междунар. науч. конф. (г. Москва, июнь 2015 г.). — Москва : Буки-Веди, 2015. — С. 175-178. — URL: https://moluch.ru/conf/ped/archive/151/8209/ (дата обращения: 02.05.2024).
Основу инженерного образования обучающихся по направлению «Строительство» составляют такие дисциплины как «Теоретическая механика» и «Сопротивление материалов». Они являются первостепенной основой технического образования и позволяют овладеть «Строительной механикой», «Механикой грунта» и рядом других технических дисциплин, связанных с расчетом элементов конструкций, зданий и сооружений.
В начале обучения, когда студент еще мало имеет представления об области технических задач, которые ему предстоит решать, у будущего строителя возникает вопрос, зачем ему необходимо изучать такие разделы как «Кинематика» и «Динамика» в теоретической механике, или «Динамические задачи» сопротивления материалов, ведь здания и сооружения — условно неподвижные конструкции. С неохотой студенты относятся к изучению характеристик движения, изучению плоского и сферического движения, тем более законов динамики. Поэтому очень важно показать необходимость изучения данных разделов применительно к строительным конструкциям, продемонстрировать примеры применения законов динамики, возможности упрощения решения задач с их использованием, а подчас и единственный возможный способ решения.
Нельзя пренебрегать простейшим и наглядными примерами необходимости учета законов кинематики и динамики в строительных конструкциях, как например, возникновение дополнительных нагрузок на трос, удерживающий груз. Будет наглядным провести сравнение реакции, возникающей в тросе, в трех случаях, демонстрирующих сравнение задач статики и динамики (рис. 1, а) [2, с. 160].
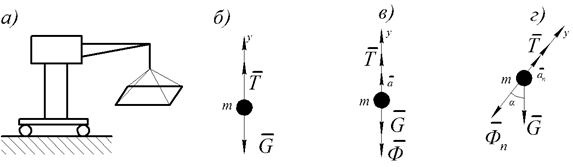
Рис. 1.
1. Статическая задача. Груз массой m подвешен к неподвижному тросу, или груз поднимается и опускается с постоянной скоростью (рис. 1, б).
V=const или V=0.
Составляем уравнение равновесия: ∑Fiy=T─ G=0;
T=G.
2. Динамическая задача 1. Момент начала подъема. Подъемный механизм создает ускорение, необходимое для достижения постоянной рабочей скорости. В соответствии с принципом Даламбера, для того, чтобы можно было составить уравнение равновесия, необходимо приложить силу инерции в сторону обратную ускорению (рис. 1, в).
0→V; а≠0; Ф=ma;
Составляем уравнение равновесия: ∑Fiy=T─ G ─ Ф=0;
Т=G+Ф.
Т=G+a∙G/g
3. Динамическая задача 2. Сильный порыв ветра. Груз начинает раскачиваться по кривой. Возникает центростремительное ускорение (рис. 1, г).
an=V2/R
Составляем уравнение равновесия: ∑Fiy=T─ Фn─ G∙Cosα=0;
T= G∙Cosα+ G∙V2/R∙g
Подстановка численных значений и сравнение реальных перегрузок, возникающих в тросе, наглядно демонстрируют важность учета динамических процессов при расчетах, объясняют причины возможных поломок при запуске грузоподъемных механизмов. При объяснении решения важно подчеркнуть, что без принципа Даламбера решение подобных задач вообще невозможно [1,с.180–200], [2, с 157].
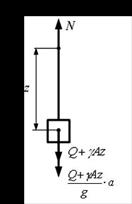
Рис. 2
Сила натяжения троса в сечении на расстоянии z от нижнего конца обусловлена статической нагрузкой от веса груза Q и веса троса γАz, а также инерционной нагрузкой a∙(Q+γАz)/g. Следовательно, продольная сила определяется как:
N=Q+γАz+a∙(Q+γАz)/g,
а нормальное напряжение в сечении троса равно:
σ=(1+a/g)∙(Q+γАz)/A.
Наглядным объяснением важности изучения законов кинематики и динамики является демонстрация их применения для решения задач статики и упрощение этого решения по сравнению с использованием методов статики. Одним из таких примеров является принцип возможных перемещений, который позволяет продемонстрировать необходимость изучения плоского движения для вывода связей между перемещениями точек тела и возможность решения задач статики методами динамики. При этом демонстрационные примеры не обязательно должны быть громоздкими.
Например, на штангу АВ (рис. 3, а) шатунно-балансировочного механизма действует сила F и необходимо определить момент m пары сил, которую следует приложить к балансиру OE длиной l, чтобы уравновесить механизм в положении, когда угол ОАЕ=β, а угол ЕАВ=α. Весом звеньев и трением пренебрегаем. Решение задачи можно провести двумя способами.
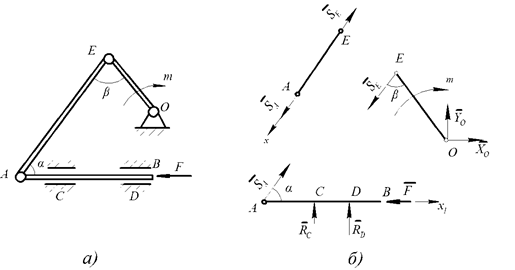
Рис. 3
Применяя методы статики, рассмотреть равновесие стержня АЕ, АВ и ОЕ и составить соответствующие три уравнения равновесия:
∑Fiх = SA─ SЕ=0;
∑Fiх1 = SA∙Cosα─ F=0;
∑mO(Fi)= SЕ∙Sinβ─ m=0;
Решая данную систему, получим m=F∙l∙Sinβ/Cosα.
Применяя принцип возможных перемещений (рис. 4), необходимо составить только одно уравнение:
F∙δSА─ m∙δφ=0. Откуда m= F∙δSА/δφ.
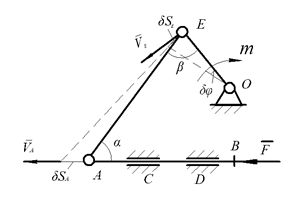
Рис. 4
Учитывая, что звено АЕ совершает плоское движение, находим связь между скоростями точек А и Е, и соответственно связь между перемещениями δSА и δφ.
ωОЕ= υЕ/l; → δφ= δSЕ/l;
По теореме о проекциях скоростей точек на прямую АЕ:
υА∙Cosα=υЕ∙Sinβ; → δSА∙Cosα=δSЕ∙Sinβ;
Тогда δSА/δφ=Sinβ/Cosαи m=F∙l∙Sinβ/Cosα.
Принцип возможных перемещений также очень хорошо позволяет продемонстрировать сокращение решения задач статики при его использовании. Например, на рис. 5, а изображена конструкция, состоящая из четырех одинаковых Т-образных рам, соединенных шарнирами К, М, Q. Опоры А и Е — шарнирно-неподвижные, В и D — шарнирно-подвижные и необходимо определить горизонтальную составляющую 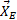 реакции опоры Е, вызванную силой
реакции опоры Е, вызванную силой 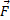 , приложенной к левой раме.
, приложенной к левой раме.
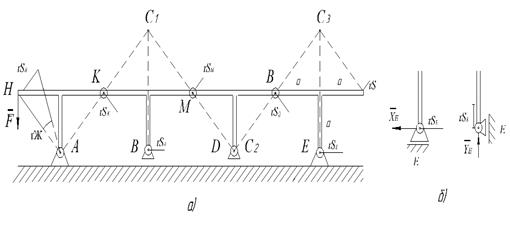
Рис. 5
Методы статики дадут довольно сложное и длинное решение, так как придется рассматривать равновесие четырех рам и решать систему из 12 уравнений с 12-ю неизвестными. Принцип возможных перемещений дает более простое и короткое решение [2, с.132], [3, с.213].
Изменив конструкцию опоры Е, сделаем ее подвижной. Чтобы система осталась в равновесии, приложим к опоре неизвестную искомую силу 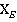 , (рис. 5, б). Задаем системе возможное перемещение, повернув левую раму вокруг опоры А на угол
, (рис. 5, б). Задаем системе возможное перемещение, повернув левую раму вокруг опоры А на угол 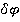 . С помощью мгновенных центров скоростей С1, С2 и С3 каждой рамы, определяем, что
. С помощью мгновенных центров скоростей С1, С2 и С3 каждой рамы, определяем, что
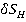 =
=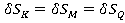 , а
, а 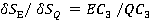
или 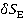 =(
=(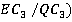 ·
·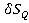 =(2а·
=(2а·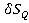 /а
/а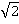 )·
)·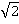
Составляем уравнение работ, общее уравнение статики:
─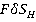 ·
·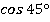 =
=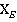 ·
·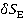 =0;
=0;
или ─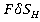 ·
·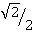 ─
─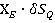 ·
·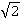 =0;
=0;
Откуда 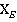 = ─1/2F.
= ─1/2F.
Таких примеров можно привести много по каждому из изучаемых разделов кинематики и динамики, демонстрируя важность этих разделов для обучающихся по направлению «Строительство».
Также необходимо объяснить студентам, что огромное значение для практики представляют задачи об учете и анализе динамического поведения конструкций, вызванного наличием переменных во времени силовых нагрузок, которые могут быть подвижными, переменными по величине или направлению или носить случайный характер. Учет динамического фактора в поведении конструкции часто бывает решающим в анализе её надежности и функциональности, так известно множество фактов потери устойчивости, а то и разрушения равновесных конструкций типа мостовых или трубопроводных пролетов, из-за недостаточного динамического анализа на этапе их проектирования. Примеры подобных задач позволят продемонстрировать важность изучения таких разделов как: колебательное движение, теории удара и ряда других разделов динамики.
Для будущего строителя все разделы теоретической механики важны. Преподавателю необходимо это доказать, заинтересовав студента наглядными примерами и демонстрацией применения соответствующих методов и законов к расчету строительных конструкций.
Литература:
1. Строительная механика. В 2 т.: учебник для студ. учреждений высш. проф. образования / В. В. Бабанов — 2-е изд. стер. — М.: Издательский центр «Академия», 2012. — 303 с. — (сер. Бакалавриат)
2. Сопротивление материалов: лекции, семинары, расчетно-графические работы: учебник для бакалавров/ С. Н. Кривошапко. — М.: Издательство Юрайт, 2012. — 413 с. — Серия: Бакалавр.
3. Молотников В. Я. Механика конструкций. Теоретическая механика. Сопротивление материалов: Учебное пособие. — Спб.: Издательство «Лань», 2012.- 544 с.: ил. — (Учебники для вузов. Специальная литература)
Похожие статьи
Исследование статической задачи несимметричной теории...
1. Новая постановка задачи несимметричной теории упругости. Уравнения движения.
1. Основными уравнениями являются два уравнения равновесия и два уравнения сплошности, записанные в напряжениях.
Антиплоская задача для упругой полуплоскости с жестким...
Механика упругой среды или теории упругости занимается деформацией и движением
Фундаментальная функция уравнения (3) имеет вид (5), через которую решение задачи (3) запишется в виде.
Динамические напряжения и смещения вблизи цилиндрической...
Осесимметричная динамическая задача о нагружении...
Осесимметричная динамическая задача о нагружении упруго-пластической сферы под действием подвижной нагрузки.
где — компоненты псевдовязкостных напряжений. Уравнения движения выводятся на
2. Зенкевич О. Метод конечных элементов в технике. М., «Мир»,1975.
Ключевые слова: развивающее обучение, теоретическая механика
2. История развития механики. 3. Основные понятия и определения механики и статики.
3. Назовите методы теоретической механики, которыми пользуется она при изучении движения тел.
Студент составил уравнения равновесия, решил их
Динамические напряжения и смещения вблизи цилиндрической...
В этой работе изучается поле динамических напряжений и смещений, возникающее вблизи
Уравнение (13) решается методом Гаусса с выделением главного элемента [14].
Авлиякулов Н. Н., Сафаров И. И. Современные задачи статики и динамики подземных трубопроводов.
Решение некоторых классических пространственных задач теории...
1. Основными уравнениями являются два уравнения равновесия и два уравнения сплошности, записанные в напряжениях.
Осесимметричная динамическая задача о нагружении...
Нелинейные колебания резиновой мембраны | Статья в журнале...
Решается динамическая задача о растяжении нормальным давлением мембраны из
Строится решение для малых колебаний около статического положения равновесия. Решение нелинейных динамических уравнений строится с применением метода сеток.
Технология развивающего обучения в вузах | Статья в сборнике...
Рассмотрение важнейших задач теории устойчивости движения принадлежат А. М
2. История развития механики. 3. Основные понятия и определения механики и статики.
3. Назовите методы теоретической механики, которыми пользуется она при изучении движения тел.
Исследование статической устойчивости Навоийской ТЭС...
Расчетную процедуру можно упросить, а получаемые результаты усилить совместным применением данного метода и метода уравнений узловых напряжений [11].
Общая задача об устойчивости движения. М — Л. Гость. Издательство тех- теор. аит, 1950.
Похожие статьи
Исследование статической задачи несимметричной теории...
1. Новая постановка задачи несимметричной теории упругости. Уравнения движения.
1. Основными уравнениями являются два уравнения равновесия и два уравнения сплошности, записанные в напряжениях.
Антиплоская задача для упругой полуплоскости с жестким...
Механика упругой среды или теории упругости занимается деформацией и движением
Фундаментальная функция уравнения (3) имеет вид (5), через которую решение задачи (3) запишется в виде.
Динамические напряжения и смещения вблизи цилиндрической...
Осесимметричная динамическая задача о нагружении...
Осесимметричная динамическая задача о нагружении упруго-пластической сферы под действием подвижной нагрузки.
где — компоненты псевдовязкостных напряжений. Уравнения движения выводятся на
2. Зенкевич О. Метод конечных элементов в технике. М., «Мир»,1975.
Ключевые слова: развивающее обучение, теоретическая механика
2. История развития механики. 3. Основные понятия и определения механики и статики.
3. Назовите методы теоретической механики, которыми пользуется она при изучении движения тел.
Студент составил уравнения равновесия, решил их
Динамические напряжения и смещения вблизи цилиндрической...
В этой работе изучается поле динамических напряжений и смещений, возникающее вблизи
Уравнение (13) решается методом Гаусса с выделением главного элемента [14].
Авлиякулов Н. Н., Сафаров И. И. Современные задачи статики и динамики подземных трубопроводов.
Решение некоторых классических пространственных задач теории...
1. Основными уравнениями являются два уравнения равновесия и два уравнения сплошности, записанные в напряжениях.
Осесимметричная динамическая задача о нагружении...
Нелинейные колебания резиновой мембраны | Статья в журнале...
Решается динамическая задача о растяжении нормальным давлением мембраны из
Строится решение для малых колебаний около статического положения равновесия. Решение нелинейных динамических уравнений строится с применением метода сеток.
Технология развивающего обучения в вузах | Статья в сборнике...
Рассмотрение важнейших задач теории устойчивости движения принадлежат А. М
2. История развития механики. 3. Основные понятия и определения механики и статики.
3. Назовите методы теоретической механики, которыми пользуется она при изучении движения тел.
Исследование статической устойчивости Навоийской ТЭС...
Расчетную процедуру можно упросить, а получаемые результаты усилить совместным применением данного метода и метода уравнений узловых напряжений [11].
Общая задача об устойчивости движения. М — Л. Гость. Издательство тех- теор. аит, 1950.











