Математическое исследование динамики индикатора эффективности банковского кредитования

Деятельность коммерческого банка ориентирована на получение прибыли, увеличение рентабельности капитала и снижение затрат на банковские операции. Прирост прибыли банка и увеличение эффективности использования его средств обусловлены процессами формирования доходов, расходов и финансовых результатов деятельности банка, которые обычно представляют собой нелинейную функцию. Устойчивость работы банка определяется величиной риска, кредитным потенциалом и надежностью заемщиков.

Для оценки устойчивости банка с точки зрения эффективности кредитных операций вводится индикатор эффективности банковского кредитования, полученный в результате математического моделирования.

Наиболее подходящей формой аппроксимации функции прибыли банка от величины кредитного потенциала является обратно пропорциональная зависимость. С увеличением кредитного потенциала банка доходы возрастают неодинаковыми темпами и поэтому изменение прибыли можно представить в виде уравнения гиперболы:

, (1)

где P – прибыль банка от кредитования, – объем кредитного портфеля банка, a и b – эмпирические параметры модели.

Расширение долговых обязательств в активах банка пропорционально увеличивает риск, связанный с нарушением условий кредитного договора. С увеличением объема выданных кредитов растет сумма невозвратов по выданным банковским займам. Функциональную зависимость объема кредитного портфеля и убытков, причиненных банку вследствие нарушения заемщиками принятых обязательств, можно описать с помощью линейной функции:

(2),

где L – сумма потерь от невозвратов по кредитам, а – доля невозвратов по кредитам.

В результате алгебраического сложения функций (1) и (2) получаем уравнение линии второго порядка:

, (3)

где I – прибыль банка от кредитования, уменьшенная на величину потерь от невозвратов по кредитам.

Таблица

Значения кредитного потенциала, прибыли, объема невозвратов по кредитам (k=0,01, 0,05, 0,1) и прибыли банка, уменьшенной на величину потерь от невозвратов, млрд. руб.

В таблице приведены исходные данные для расчета параметров модели и индикаторов эффективности банковского кредитования. В столбце (1) указан год, в столбце (2) кредитный потенциал банка, в столбце (3) прибыль банка. В столбцах (4), (6) и (8) рассчитана величина невозврата по кредитам на указанный год и при заданном значении доли невозвратов по кредитам. В столбцах (5), (7) и (9) – значение прибыли, уменьшенной на величину невозвратов по кредитам.

Банк в период с 2004-2008 гг. наращивает кредитный портфель. Допустим, доля невозвратов по кредитам составляет 0,01, 0,05 и 0,1 от величины кредитного потенциала. Прибыль банка в ситуациях с долей невозвратов 0,01 и 0,05 возрастает замедляющимися темпами (т.е. имеет место эффект насыщения). Прибыль банка при невозврате 0,1 кредитов снижается и превращается в убыток. Невозвраты по кредитам увеличиваются пропорционально кредитному потенциалу. Эти рассуждения относятся к интервалу кредитного потенциала банка от 11,1 до 19,6 млрд. руб. и иллюстрированы в виде математических моделей на графике 1.

Для исследования этих процессов на основе данных таблицы методом наименьших квадратов были получены численные значения коэффициентов регрессии функции (1):

Затем, для различных значений доли невозврата (k) определяем функцию L (2). Путем алгебраического сложения функций P и L получаем окончательную модель I (3). В точке экстремума прибыль банка, уменьшенная на величину невозвратов по кредитам, имеет максимум, то есть производная функции I равна нулю: .

(4)

Оценим влияние изменения доли невозвратов по кредитам на точку максимума эффективности кредитования. Если доля невозвратов составляет k, то максимум эффективности достигается при объеме и соответствует ндикатору I*. Таким образом, изменение доли невозвратов по кредитам приведет к изменению Q* и I*. Увеличение доли невозвратов по выданным ссудам приведет к смещению Q* влево и снижению величины I*, и наоборот – снижение доли невозвратов по кредитам приведет к смещению Q* вправо и увеличению I*. Проиллюстрируем это с помощью графика.

Г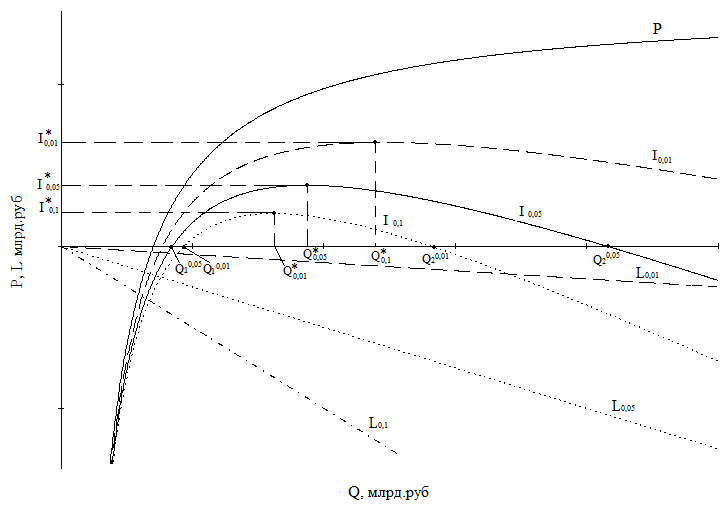рафик 1. Модель индикатора эффективности банковского кредитования при значениях k=0,01, 0,05 и 0,1

На графике 1 показана кривая прибыли банка (P), полученная на основе модели (1), прямые убытков банка (L), полученные на основе модели (2) и линии второго порядка I, полученные на основе модели (3) для трех значений доли невозвратов по кредитам (k).

Рассчитаем значение кредитного потенциала, при котором эффективность кредитования достигает максимума. При наименьшей принятой для анализа модели доли невозвратов k=0,01, по формуле (4) получаем млрд. руб. Такой величине кредитного потенциала соответствует млрд. руб. При изменении доли невозвратов, полученная величина кредитного потенциала меняется. Предположим, что невозвраты по кредитам возросли с 0,01 до 0,1. Кредитный потенциал будет равным млрд. руб. При этом значении Q* индикатор эффективности банковского кредитования I* будет равняться 1,613 млрд. руб. Расчеты доказывают, что при увеличении доли невозвратов по кредитам величина индикатора достигается при меньшей величине объема кредитного портфеля и при меньшем значении прибыли.

Г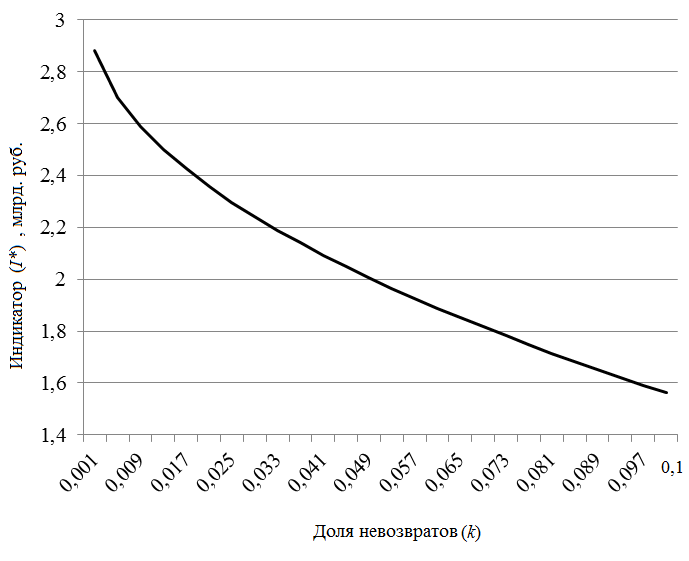рафик 2. График величины максимума кредитного потенциала в зависимости от доли невозвратов

На графике 2 представлена кривая, характеризующая изменения значений индикатора (млрд. руб.) при различных величинах доли невозвратов от 0,001 до 0,1.

Изменение величины невозвратов в большую сторону существенно снижает эффективность кредитования. Кредитный потенциал, при котором достигается максимум эффективности, уменьшается. Значение расчетной прибыли при максимальном значении эффективности также уменьшается.

Проанализируем модель индикатора эффективности банковского кредитования с точки зрения безубыточности. На графике 1 показаны две точки и . Обе они подпадают под определение точек безубыточности – точек, при которых доходы от кредитных операций равны величине невозвратов по ссудам. Однако характер этих точек принципиально разный. При любом объеме кредитного портфеля, лежащем слева от точки , банк несет убытки от кредитных операций. При возрастании объема кредитования и переходе через точку банк начинает получать прибыль. На интервале (,) доходы банка превышают убытки от невозврата по ссудам. В этом интервале прибыль достигает своего максимума в точке и в последующем снижается до точки . Прибыль банка равна нулю при объеме остатков задолженности по ссудам равном . Дальнейшее расширение кредитования вновь делает операции банка убыточными.

Любые изменения платежеспособности заемщиков непосредственно определяют величину и . В периоды экономического спада платежеспособность экономических агентов падает, вследствие чего возрастает доля невозвратов по кредитам , в результате чего убытки банков растут. Находясь на уровне безубыточности увеличение не так отрицательно отразится на устойчивости банка, как в случае состояния . Увеличение доли невозвратов для банка с объемом кредитного портфеля приведет к неизбежным высоким убыткам и серьезным угрозам ликвидности банка.

Данные выводы подтверждаются расчетами величин точек и . При величине доли невозвратов по кредитам 0,01 банк достигает уровня безубыточности при значениях кредитного потенциала 7,1 млрд. руб. () и 299,9 млрд. руб. (). Если величина доли невозвратов возрастает до 0,05, то значения и составят 7,94 млрд. руб. и 53,5 млрд. руб. соответственно.

Также график 1 показывает, что интервал величины кредитного потенциала, при котором банк будет получать прибыль, уменьшается. Если при доле невозвратов, равной 0,01 ∆Q= Q₂-Q₁=299,9-7,1=292,8 млрд. руб., то увеличение доли невозвратов по ссудам до 0,05 интервал, на котором банк может получать прибыль, существенно сокращается ∆Q=Q₂-Q₁=53,5-7,94=45,56 млрд. руб.

Кредитные операции являются одним из основных источников прибыли коммерческого банка. Поэтому для банка важна оценка эффективности кредитования и поиск путей ее повышения. Предложенная модель индикатора экономической эффективности имеет высокие адаптационные возможности для мониторинга финансовой устойчивости и на его основе позволяет своевременно корректировать деятельность банка.