Современные производственные объект представляют собой сложную систему, состоящую из совокупности взаимосвязанных многорежимных подсистем, функционирование которых направлено на достижение общих целей системы. Особенностями такой производственной системы являются: наличие выделяемых частей (подсистем, элементов), для каждой из которых может быть определена цель функционирования; участие в работе системы людей, машин и среды; существование внутренних материальных, энергетических и информационных связей между частями системы, а также внешних связей рассматриваемой системы с другими объектами.
Большинство производственных комплексов, в которых протекают различные процессы, функционируют в условиях неопределенности. Эта неопределенность возникает по ряду причин, основными из которых являются:
- сложность объекта и недостаточная изученность процессов протекающих в нем;
- стохастическая природа основных параметров, описывающих функционирования объекта;
- наличие большого количества возмущающих воздействий и помех на производстве, зашумленность информации;
- недостаточная достоверность исходной статистической информации, обусловленная низкой надежностью, нехватки или отсутствием промышленных средств сбора и обработки такой информации;
- недостатки методов обработки информации;
- плохоформализуемые действия человека, участвующего в контуре управления, и субъективность его действий при принятии решений;
- нечеткость, качественный характер собранной у специалистов информации, описывающей состояние объекта;
- наличие нечетких ограничений и критериев оптимизации.
Неопределенность можно проклассифицировать различными способами, они представлены на рисунке 1:
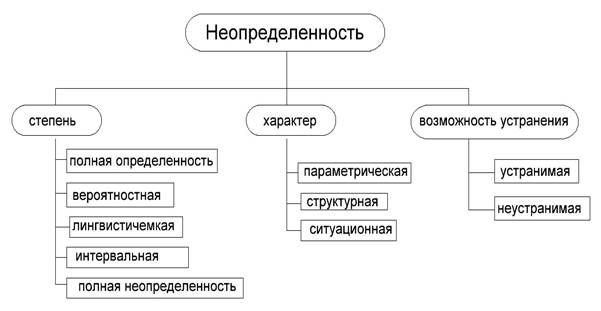
Рис. 1. Классификация неопределенностей
Таким образом, основными источниками неопределенности в производственных условиях являются недостаточность и нечеткость исходной информации.
Одним из важнейших этапов реализации управления является синтез систем автоматического управления (САУ) и построение их адекватных математических моделей. От правильности или удачности выбора модели во многом зависит весь ход дальнейших исследований САУ. Конечно, при построении модели, желательно получить ее четкое математическое описание. Однако, попытки получить четкое математическое описание САУ в тех случаях, когда иная информация о них, кроме нечеткой, недоступна, путем задания строгих границ «волевым» методом или искусственным введением однозначности, приводит к огрублению исходных данных, которое может способствовать получению четких, но не адекватных моделей и поэтому не целесообразны. Тем не менее и в этом случае целесообразно попытаться выделить в нечеткой в целом САУ отдельные ее части, поддающиеся четкому математическому описанию.
Таким образом, уже в самом начале процесса построения модели следует ответить на вопрос, какой тип модели четкий или нечеткий может быть получен исходя из имеющейся информации об изучаемой САУ в целом и об ее отдельных составляющих частей. В случае наличия принципиальной возможности получения четкой модели САУ в целом или ее отдельных частей, следует начинать построения одной из следующих четких моделей.
Непрерывные линейные модели, описывающиеся системой линейных, обыкновенных дифференциальных уравнений состояния вида:
,
где: у — 
-мерный вектор состояния системы; 
– m-мерный вектор задания на управление; 
— 
-мерный вектор управляющего воздействия; 
– 
-мерный вектор возмущающих воздействий; А — (
)-мерная постоянная матрица; В — (
)-мерная постоянная матрица; С — (
)-мерная постоянная матрица; D — (
)-мерная постоянная матрица.
Для систем с запаздыванием переменных состояния или воздействий уравнения состояния представляют собой систему дифференциально-разностных уравнений вида:
,
где: 
,
, 
, 
— время запаздывания соответствующего вектора.
К таким системам применим принцип суперпозиции и поэтому можно действия на систему векторов 
изучать раздельно. Это явилось следствием того, что подобные системы описываются обычно уравнением вида:
,
или:
.
Ограничения в таких системах так же линейны:
где: s, h — линейные векторные функции.
Соответственно и целевая функция таких систем должна быть линейной:
,
где 
— линейная скалярная функция. Обычно целевая функция в этих системах является показателем качества, выражаемым скалярной величиной вида:
,
где: 
и 
— скалярные функции, а 
и 
— начальный и конечный моменты времени соответственно
Случаи, когда ограничения или целевая функция не линейны относятся к непрерывным нелинейным системам, а случаи, когда целевая функция векторная — относятся к интеллектуальным нечетким системам.
Аналитическое решение уравнения состояния известно:
,
где 
– вектор начального состояния системы в момент времени 
.
Поэтому формализация описания САУ в этом виде является наиболее предпочтительным, но, к сожалению, редко достижимым.
Непрерывные нелинейные модели, описывающиеся системой нелинейных обыкновенных дифференциальных уравнений первого порядка вида:
,
где 
— -мерная нелинейная векторная функция.
Непрерывные нелинейные системы с запаздыванием описываются соответственно системой дифференциально-разностных уравнений:
.
В этом случае ограничения 
, 
и целевая функция в могут быть нелинейными. Причем желательно, чтобы ограничения, образовывали выпуклые множества, функция была выпуклой или вогнутой, так как в противном случае традиционные вычислительные методы поиска оптимальных решений не дают гарантированного результата за приемлемой число итераций и требуется использовать новые интеллектуальные методы поиска оптимальных решений, например генетические алгоритмы.
Аналитического решения уравнений получить, как правило, не удается. Однако существует достаточно обширный класс систем, для которых удается получить численные решения достаточной точности за приемлемое число итераций.
Дискретные линейные модели при постоянном временном интервале могут быть описаны следующей системой разностных уравнений состояния:
,
где 
и — номера интервалов времени.
Вектор состояния 
в любой дискретный момент времени 
может быть определен в виде функции начального состояния и всех предшествующих векторов, например при 
и 
имеем:
.
Ограничения в каждый дискретный момент времени в этом случае имеют вид:
,
где: 
— линейные векторные функции.
Целевая функция принимает вид:
,
где — скалярная линейная функция.
Формализованное описание дискретных САУ в этом виде наиболее желательно, так как задачу синтеза оптимальной системы в этом случае обычно можно свести к задаче линейного программирования.
Дискретные нелинейные модели описываются следующими разностными уравнениями состояния:
где: 
– номер временного интервала.
В каждый дискретный момент времени система должна быть подчинена дополнительной системе ограничений:
,
где 
и 
— в общем случае нелинейные функции.
В этом случае функция для целевой функции может быть нелинейной. Аналитического решения системы в общем случае не имеется. Однако существует класс систем, для которых можно получить достаточно точные численные решения. Очевидно, что и в этом случае желательно, чтобы ограничения и образовывали выпуклые множества, а функция была выпуклой или вогнутой.
Стохастические модели используются для САУ со случайными параметрами или для САУ со случайными возмущающими воздействиями.
Системы со случайными параметрами можно описывать непрерывными и дискретными линейными или нелинейными моделями подобными предыдущим. Однако уравнения состояния, ограничений и целевых функций в этом случае записываются для статистических оценок параметров, наиболее используемыми из которых являются оценки математических ожиданий и дисперсий. В системах со случайными возмущающими воздействиями широко используются такие характеристики входных воздействий и выходных реакций системы, как корреляционные функции и спектральные плотности случайных функций времени. Однако при этом случайные входные воздействия должны обладать свойствами стационарности и эргодичности. В противном случае указанные характеристики становятся неопределенными, и тогда САУ приходится описывать нечеткими моделями.
Нечеткие модели используются при отсутствии принципиальной возможности получения четкой модели САУ или каких либо ее частей. Выбор нечеткой модели во многом зависит от выявленных неопределенностей в САУ.
После выявления имеющихся в данной задаче анализа и синтеза САУ неопределенностей может быть построена одна из следующих нечетких моделей
Логико-вероятностные модели с не изменяющимися вероятностями событий, описывающиеся системами логических уравнений или системами алгебраических уравнений по модулю 2. При этом логические переменные имеют в качестве атрибутов вероятности их истинности или ложности, которые не изменяются во времени. Систему логических уравнений обычно приводят к уравнениям вида линейной последовательностной машины.
Логико-вероятностные модели с изменяющимися во времени вероятностями событий так же описываются системами логических уравнений или алгебраических уравнений по модулю 2. Однако процесс вычисления минимума целевой функции при изменении во времени вероятностей событий усложняется, так как в этом случае целевая функция так же изменяется во времени. Последнее обстоятельство является характерной чертой систем эволюционно-генетического типа или человеко-машинных систем.
Логико-вероятностные модели с интервальным заданием вероятностей описываются системами логических или алгебраических по модулю 2. Однако процесс вычисления минимума целевой функции резко усложняется, так как вероятности каждого из возможных исходов теперь лежат в некоторых диапазонах, вычисление которых зависит от логического уравнения, из которого получена данная логическая величина исходов.
Логико-вероятностные модели с интервальным заданием вероятностей, меняющимся во времени так же описываются системами логических уравнений или алгебраических уравнений по модулю 2. Однако процесс вычисления минимума целевой функции при изменении во времени интервалов вероятностей событий усложняется, так как в этом случае целевая функция так же изменяется во времени. Такие модели характерны для ЧМС. Построение адекватных моделей таких систем связано с изучением поведения ЛПР и требует их предварительного тестирования с целью выявления характерных особенностей поведения при принятии решения в условиях неполной определенности.
Логико-вероятностные модели со случайными вероятностями событий описываются системами логических или алгебраических по модулю 2 уравнений.
Логико-лингвистические модели с неизменяющимися во времени функциями принадлежности описываются системами логических или алгебраических по модулю 2 уравнений.
Логико-лингвистические модели с изменяющимися во времени функциями принадлежности описываются аналогично предыдущим. Однако из-за изменения функций принадлежности во времени необходимо во-первых расчеты производить на порядок быстрее скорости изменения функций принадлежности, а во-вторых постоянно периодически повторять расчеты для коррекции воздействий вслед за изменениями функций принадлежности.
Логико-лингвистические модели с не формализуемыми атрибутами лингвистического типа, для описания логической части использующие по модулю 2. Однако при этом требуется задание правил или алгоритмов обработки лингвистической атрибутной части, характеризующей нечеткость или не определенность логических переменных, при проведении над ними операций сложения и умножения по модулю 2.
В заключении следует отметить, что при исследовании и синтезе сложных САУ могут быть использованы методы идентификации, нечёткой логики и все рассмотренные виды моделей в любых сочетаниях.
Литература:
1. Лю Б. Теория и практика неопределенного программирования / Б.Лю. — М.: БИНОМ. Лаб.знаний, 2005. — 416с.
2. Моисеев Н. Н. Элементы теории оптимальных систем / Н. Н. Моисеев. — М.:Наука,1975. — 528с.
3. Рутковская Д., Плинский М., Рутковский Л., Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с польск. И. Д. Рудинского. — М.: Горячая линия — Телеком, 2006. — 452 с.
4. Управление в условиях неопределенности / Под ред. д-ра техн. наук, проф. А. Е. Городецкого. СПб.: Изд-во СПбГТУ, 2002. 398 с.
