Введение. Коррумпированные предприятия стараются скрывать свои противоправные действия, например, ведя «черную» и «белую» бухгалтерию. Распространенными примерами коррумпированных предприятий являются фирмы «однодневки» и фирмы, занимающиеся «отмыванием» средств, заработанных преступным путем. Одним из эффективных способов борьбы с коррупцией является неожиданная проверка. В работе исследуется взаимодействие коррумпированного предприятия и федерального отдела по борьбе с коррупцией.
В настоящее время метод математического моделирования широко распространен в различных областях. В работах [1, 2] исследуется процесс диффузии коррупционного капитала. В статье [3] производится построение математической модели развития компании. Модели многоагентного взаимодействия в условиях конкуренции рассмотрены в [4–8, 16, 42]. В работах [9–11] моделируются процессы реконструкции жилой застройки мегаполиса в условиях конкурентной среды. Исследование управляемых конфликтных систем производится в [12]. В статьях [13, 14] подробно рассматриваются следующие математические модели: вероятностно-детерминированная модель влияния различных факторов на функционирование организации, осуществляющей инновационную деятельность, и стохастическая модель принятия решения о выводе на рынок какого-либо инновационного продукта. В книге [15] строятся и исследуются модели взаимодействия нескольких культур. Рассмотрение математических моделей, основанных на конкуренции, производится в статьях [17–26, 30–34, 36, 37]. В статьях [28, 29] производится моделирование взаимодействия этнокультур и рассматривается принцип максимума в организаторской деятельности. В работе [35] рассматривается проблема существования обобщенного значения динамической игры. В [39] строится модель коррупции при заключении контрактов. Проблема существования значения игры преследования рассматривается в статье [41]. Решение уравнения Гальтона-Якоби для дифференциальной игры двух участников с нулевой суммой ищется в работе [43].
Постановка задачи. Рассматривается фирма A, которая занимается отмыванием денежных средств через АЗС (автозаправочную станцию). Фирма предоставляет ряд услуг: автомойка, заправка, ремонт и окраска автомобиля. Денежные средства, заработанные преступным путем, проводят через кассу. Каждый день приходят мнимые клиенты. Кассир, создавая видимость работы организации, выбивает чек на использование услуг компании и докладывает деньги в кассу.
Рассматриваются противозаконные действия фирмы в течение определенного промежутка времени,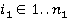 
, где 
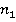— это рассматриваемый период проверок. Фирма совершает противозаконные сделки разного типа с разной прибылью от сделки. Существует 
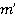типов сделок, при реализации которых фирма получает разную прибыль, 
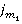— количество совершенных сделок типа 
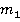, где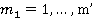 
. Будем считать, что коррупционное предприятие — это игрок I, который имеет чистую стратегию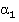 
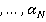где 
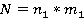с матрицей игры 
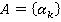, где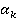 
— прибыль, которую получит коррупционное предприятие при поведении 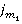сделок типа 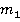в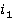 
-й день, 
.
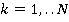В свою очередь финансовый отдел по борьбе с коррупцией занимается раскрытием преступлений такого рода. В связи с загруженностью этого отдела, один сотрудник может выделить для проверки только один день, то есть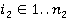 
, где 
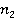— это рассматриваемый период проверок. В зависимости от раскрытия сделок определенного типа, сотрудник получает разную прибыль. Пусть 
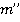— количество проверяемых сделок, тогда 
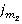количество проверенных сделок типа 
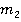, где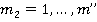 
. Будем считать, что сотрудник отдела по борьбе с коррупцией — это игрок II, который имеет чистую стратегию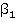 
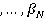, где 
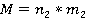с матрицей игры 
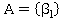, где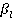 
- прибыль, которую получит сотрудник при раскрытии сделок типа 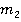(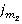) в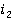 
-й день, 
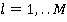, (чем крупнее раскрытая сделка, тем больше прибыль сотрудника).
Модель. Данная модель может быть представлена в виде бескоалиционной игры. Математическое ожидание выигрыша для игрока I:
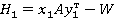
где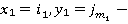 
равновесные стратегии первого игрока, 
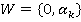— штраф, который заплатит фирма при условии раскрытия противозаконных сделок в размере 
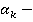прибыли, полученной в данный день. Если же противозаконных сделок не обнаружено, штраф принимаем равным нулю: 
.
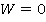Математическое ожидание выигрыша для игрока II:
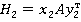
где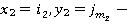 
равновесные стратегии второго игрока.
Численное решение. Пусть рассматриваемый период времени (количество дней) равно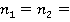 
11, количество типов сделок равно 
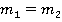=10.
Матрица игры первого игрока:
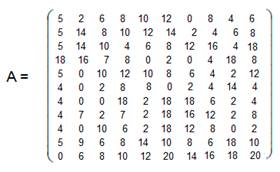
Матрица игры второго игрока:
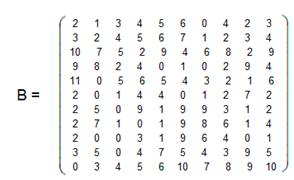
Биматричная игра, составленная из матриц A и B:
Данная матрица имеет ситуацию равновесия по Нэшу в чистых стратегиях, а именно
Математическое ожидание выигрыша каждого игрока:
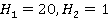
Применим принцип максимина (минимакса). Как было отмечено, каждый игрок стремится обеспечить себе максимально возможный выигрыш при любых действиях противника.
Пусть игрок I выбрал стратегию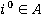 
, тогда игрок II выберет такую стратегию 
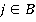, которая максимизирует его выигрыш и тем самым минимизирует выигрыш его противника. Стратегия игрока I, обеспечивающая ему наибольший выигрыш из всех возможных, независимо от действий противника, будет состоять в выборе такого 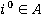, для которого минимальный выигрыш будет наибольшим, т. е.
.
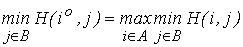Величину
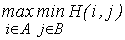
принято обозначать через v и называть нижним значением (нижней ценой) игры, а соответствующую этому значению стратегию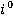 
игрока I — максиминной стратегией. Если игрок I придерживается данной стратегии, то его выигрыш будет не меньше максиминного значения, то есть
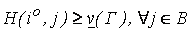(1)
Аналогично стратегия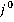 
, определяемая равенством
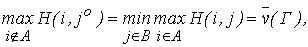(2)
называется минимаксной стратегией игрока II, а соответствующее значение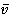 
— верхним значением (верхней ценой) игры.
Если игрок II придерживается данной стратегии, то его проигрыш будет не больше минимаксного значения, т. е.
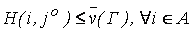(3)
Полагая, что в неравенстве (2)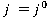 
, а в выражении (3) 
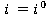, получим:
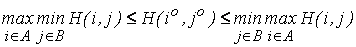
Найдем максиминные и минимаксные стратегии для каждой матрицы.
v =5, 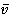=14;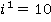 
— максиминная стратегия, 
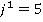— минимаксная стратегия.
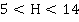
Так как v <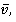 
максиминная и минимаксная стратегии не являются оптимальными.
Аналогично для второй матрицы:
v =2, 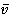=5;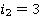 
— максиминная стратегия, 
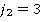— минимаксные стратегии.
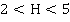
Так как v < 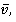максиминная и минимаксная стратегии не являются оптимальными.
Для нахождения смешанных стратегий для матрицы А воспользуемся пакетом прикладных программ Gambit:
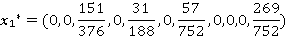
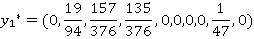
Математическое ожидание выигрыша находим по формуле:
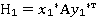
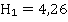
Это означает, что если фирма A будет использовать свои равновесные стратегии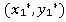
, то получит прибыль 
.
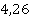Оптимальные смешанные стратегии и значение игры для матрицы B:
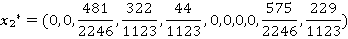
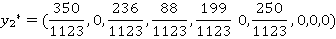
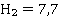
Таким образом, математическое ожидание выигрыша при выборе равновесных стратегий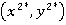 
равно .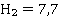
Заключение. Таким образом, в работе исследовано взаимодействие коррумпированного предприятия и федерального отдела по борьбе с коррупцией. Модель представлена в виде бескоалиционной игры. Рассмотрен численный пример.
Литература:
1. Townsend R. Propagation of Financial Shocks: The Case of Venture Capital // Tuck School of Business Working Paper. 2012. No. 2012–108. 66 p.
2. Gonzalez-Uribe J. Venture Capital and the Diffusion of Knowledge. 2013. 59 p.
3. Малафеев О. А., Черных К. С. Математическое моделирование развития компании // Экономическое возрождение России. 2004. № 1. С. 60.
4. Малафеев О. А., Соснина В. В. Модель управления процессом кооперативного трехагентного взаимодействия // Проблемы механики и управления: Нелинейные динамические системы. 2007. № 39. С. 131–144.
5. Григорьева К. В., Малафеев О. А. Динамический процесс кооперативного взаимодействия в многокритериальной (многоагентной) задаче почтальона // Вестник гражданских инженеров. 2011. № 1. С. 150–156.
6. Малафеев О. А., Зенович О. С., Севек В. К. Многоагентное взаимодействие в динамической задаче управления венчурными строительными проектами // Экономическое возрождение России. 2012. № 1. С. 124–131.
7. Парфенов А. П., Малафеев О. А. Равновесное и компромиссное управление в сетевых моделях многоагентного взаимодействия // Проблемы механики и управления: Нелинейные динамические системы. 2007. № 39. С. 154–167.
8. Грицай К. Н., Малафеев О. А. Задача конкурентного управления в модели многоагентного взаимодействия аукционного типа // Проблемы механики и управления: Нелинейные динамические системы. 2007. № 39. С. 36–45.
9. Дроздова И. В., Малафеев О. А., Дроздов Г. Д. Моделирование процессов реконструкции жилищно-коммунального хозяйства мегаполиса в условиях конкурентной среды. СПб.: Санкт-Петербургский государственный университет сервиса и экономики, 2008. 147 с.
10. Дроздова И. В., Малафеев О. А., Паршина Л. Г. Эффективность вариантов реконструкции городской жилой застройки // Экономическое возрождение России. 2008. № 3. С. 63–37.
11. Акуленкова И. В., Дроздов Г. Д., Малафеев О. А. Проблемы реконструкции жилищно-коммунального хозяйства мегаполиса. СПб.: Санкт-Петербургский государственный университет сервиса и экономики, 2007. 187 с.
12. Малафеев О. А. Управляемые конфликтные системы. СПб.: Изд-во С.- Петерб. ун-та, 2000. 280 с.
13. Гордеев Д. A., Малафеев О. А., Титова Н. Д. Стохастическая модель принятия решения о выводе на рынок инновационного продукта // Вестник гражданских инженеров. 2011. № 2. С. 161–166.
14. Гордеев Д. А., Малафеев О. А., Титова Н. Д. Вероятностно-детерминированная модель влияния факторов на функционирование организации, осуществляющей инновационную деятельность // Экономическое возрождение России. 2011. № 1. С. 73–82.
15. Колесин И. Д. Модели взаимодействия культур и управление социокультурными процессами. Учебное пособие. СПб. НИИФ СПбГУ. 2004. 84 с.
16. Малафеев О. А., Бойцов Д. С., Рединских Н. Д., Неверова Е. Г. Компромисс и равновесие в моделях многоагентного управления в коррупционной сети социума // Молодой ученый. 2014. № 10. С. 14–17.
17. Колпак Е. П., Горыня Е. В. Математические модели «ухода» от конкуренции // Молодой ученый. 2015. № 11. С. 59–70.
18. Колпак Е. П., Горбунова Е. А., Столбовая М. В., Балыкина Ю. Е. Математическая модель логистической популяции на линейном ареале // Молодой ученый. 2014. № 3. С. 6–14.
19. Колпак Е. П., Горыня Е. В., Крылова В. А., Полежаев Д. Ю. Математическая модель конкуренции двух популяций на линейном ареале // Молодой ученый. 2014. № 12. С. 12–22.
20. Колпак Е. П., Жукова И. В., Степанова Д. С., Крицкая А. В. О численных методах решения эволюционных уравнений на примере математической модели «хищник-жертва» // Молодой ученый. 2014. № 4. С. 20–30.
21. Колпак Е. П., Селицкая Е. А., Габриелян Л. А. Математическая модель коррупции в системе «власть-общество» // Молодой ученый. 2015. № 10. С. 9–16.
22. Крылова В. А., Колпак Е. П., Сыромолотова К. И., Воротова Т. А. Математические модели формирования спортивных групп // Молодой учёный. 2015. № 8. C. 10–19.
23. Кузнецова Е. А. Влияние развития малого и среднего предпринимательства на развитие конкуренции // Молодой ученый. 2012. № 2. С. 126–128.
24. Орлова Е. В., Ульмасова И. С. Методы ценообразования и их использование на высоко конкурентном рынке // Молодой ученый. 2014. № 3. С. 495–497.
25. Цю Ш. Разработка системы управления конкурентной стратегией // Молодой ученый. 2014. № 21. С. 456–458.
26. Гордеев Д. А., Малафеев О. А., Титова Н. Д. Probabilistic and Deterministic Model of the Influence Factors the Activities of the Organization to Innovate// Экономическое возрождение России. 2011. № 1. С.73–82.
27. Григорьева К. В., Иванов А. С., Малафеев О. А. Статическая коалиционная модель инвестирования инновационных проектов // Экономическое возрождение России. 2011. № 4. С. 90–98.
28. Колесин И. Д. Моделирование взаимодействия этнокультур // Известия Российской академии наук. Теория и системы управления. 2005. № 2. С. 75–80.
29. Колесин И. Д. Принцип максимума в организаторской деятельности // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. 2008. № 4. С. 9–13.
30. Колпак Е. П., Горбунова Е. А., Балыкина Ю. Е., Гасратова Н. А. Математическая модель одиночной популяции на билокальном ареале // Молодой ученый. 2014. № 1. С. 28–33.
31. Суска А. А. Конкурентный потенциал как категория конкуренции и объект управления // Молодой ученый. 2012. № 12. С. 277–279.
32. Шоев А. Х. Некоторые аспекты конкурентной борьбы за ресурсы в мировой экономике // Молодой ученый. 2014. № 6. С. 532–534.
33. Шустов А. А. Роль инновационной деятельности в конкурентной борьбе предприятия // Молодой ученый. 2013. № 10. С. 412–416.
34. Яковлева Ю. А. Роль конкуренции в рыночной экономике // Молодой ученый. 2014. № 3. С. 610–613.
35. Малафеев О. А. О существовании обобщённого значения динамической игры. Вестник Санкт-Петербург университета. Серия 1: Математика. Механика. Астрономия. 1972. № 19. С. 41.
36. Малафеев. О. А. Муравьев. А. И. Математические модели конфликтных ситуаций и их разрешение. Санкт-Петербург. 2000.
37. Малафеев О. А., Грицай К. Н. Конкурентное управление в моделях аукционов. Проблемы механики и управления: Нелинейные динамические системы. 2004. № 36. С. 74–82.
38. Малафеев О. А., Троева М. С. Устойчивость и некоторые числовые методы в конфликтно управляемых системах. Якутск, 1999.
39. Малафеев О. А., Королева О. А. Модель коррупции при заключении контрактов. В сборнике: Процессы управления и устойчивости Труды XXXIX международной научной конференции аспирантов и студентов. Под редакцией Н. В. Смирнова, Г. Ш. Тамасяна. 2008. С. 446–449.
40. Малафеев О. А., Муравьев А. И. Моделирование конфликтных ситуаций в социально-экономических системах. Санкт-Петербург, 1998.
41. Малафеев О. А. О существовании значения игры преследования. Сибирский журнал исследования операций. 1970. № 5. С. 25–26.
42. Малафеев О. А., ЗубоваА. Ф. Математическое и компьютерное моделирование социально-экономических систем на уровне многоагентного взаимодействия (введение в проблемы равновесия, устойчивости и надежности. СПб.: Изд-во С.-Петерб.ун-та,2006.1006c.
43. Malafeyev O. A., Troeva M. S. A weak solution of Hamilton-Jacobi equation for a differential two-person zero-sum game. В сборнике: Preprints of the Eight International Symposium on Differential Games and Applications 1998. С. 366–369.
