Рассматривается модельный оператор 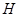 , ассоциированный с системой трех частиц на решетке, взаимодействующих с помощью парных нелокальных потенциалов. Получен аналог уравнения Вайнберга для собственных функций оператора
, ассоциированный с системой трех частиц на решетке, взаимодействующих с помощью парных нелокальных потенциалов. Получен аналог уравнения Вайнберга для собственных функций оператора 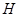 .
.
Ключевые слова: модельный оператор, нелокальный потенциал, уравнение Вайнберга, собственное значение и собственная функция, существенный спектр.
1. Введение. Исследование дискретных спектров операторов Шредингера является наиболее интенсивно изучаемым объектом в теории операторов. Одним из важных вопросов в спектральном анализе таких операторов является изучение конечности числа собственных значений, лежащих вне существенного спектра. Хорошо известно, что при некоторых естественных предположениях оператор Шредингера A системы трех попарно взаимодействующих частиц в непрерывном пространстве имеет существенный спектр, совпадающий с полуосью 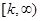 , где
, где 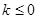 . В работах [1] и [2] доказано, что при
. В работах [1] и [2] доказано, что при 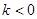 и достаточно быстром убывании потенциалов взаимодействия в координатном представлении дискретный спектр оператора является конечным. Методика [1] основана на исследовании Фpедгольмовской системы уpавнений Фаддеева и Вайнбеpга, а в работе [2] применялись вариационные соображения.
и достаточно быстром убывании потенциалов взаимодействия в координатном представлении дискретный спектр оператора является конечным. Методика [1] основана на исследовании Фpедгольмовской системы уpавнений Фаддеева и Вайнбеpга, а в работе [2] применялись вариационные соображения.
Вопросу конечности дискретного спектра трехчастичного дискретного оператора Шредингера посвящены многие работы, например [3,4]. Отметим, что в работе [3] пользуясь уравнениями типа Фаддеева и Вайнберга, а также аналитическим продолжением определителя Фредгольма, доказана конечность дискретного спектра трехчастичного дискретного оператора Шредингера парными контактными взаимодействиями при отсутствии виртуальных уровней у операторов, описывающих двухчастичных подсистем.
В работе [5] рассматривается модельный оператор 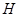 действующий в гильбертовом пространстве квадратично интегрируемых симметричных функций, определенных на
действующий в гильбертовом пространстве квадратично интегрируемых симметричных функций, определенных на 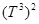 . Этот модель ассоциирован с системой трех частиц на решетке, взаимодействующих с помощью парных нелокальных потенциалов. Там построен «симметризованный» вариант известного уравнения Вайнберга, с помощью которого доказывается конечность дискретного спектра оператора
. Этот модель ассоциирован с системой трех частиц на решетке, взаимодействующих с помощью парных нелокальных потенциалов. Там построен «симметризованный» вариант известного уравнения Вайнберга, с помощью которого доказывается конечность дискретного спектра оператора 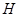 . Следует отметить, что этот метод используется даже в том случае, когда существенный спектр модельного оператора
. Следует отметить, что этот метод используется даже в том случае, когда существенный спектр модельного оператора 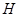 имеет лакуну. Тем самым оно является удобным методом доказательства конечности дискpетного спектpа.
имеет лакуну. Тем самым оно является удобным методом доказательства конечности дискpетного спектpа.
В данной работе рассматривается несимметризованный аналог оператора 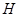 изученный в работе [5] и строится соответствующие уравнение, представляющее собой аналог известного уравнения Вайнберга, для собственных функций. Здесь ядра нелокальных операторов взаимодействия имеют ранг 1 и роль двухчастичного дискретного оператора Шредингера играет модель Фридрихса. Напомним, что для периодического оператора нелокальные потенциалы представляют собой сумму локального потенциала и некоторого конечномерного оператора. Отметим, что для многочастичных гамильтонианов нелокальные потенциалы в импульсном представлении являются частично-интегральными операторами. При этом получено очень мало результатов для таких гамильтонианов в том случае, когда ядро частично-интегрального оператора является невырожденным. В настоящее время представляет интерес получение точных результатов хотя бы для частных случаев, т. е. для нелокальных потенциалов с вырожденными ядрами. Так как двухчастичные и трехчастичные уравнения Шредингера легко разрешимы для нелокальных взаимодействий, их часто используют в ядерной физике и в многочастичных проблемах. Они также используются систематически вместе с уравнениями Фаддеева и Вайнберга для систем трех частиц.
изученный в работе [5] и строится соответствующие уравнение, представляющее собой аналог известного уравнения Вайнберга, для собственных функций. Здесь ядра нелокальных операторов взаимодействия имеют ранг 1 и роль двухчастичного дискретного оператора Шредингера играет модель Фридрихса. Напомним, что для периодического оператора нелокальные потенциалы представляют собой сумму локального потенциала и некоторого конечномерного оператора. Отметим, что для многочастичных гамильтонианов нелокальные потенциалы в импульсном представлении являются частично-интегральными операторами. При этом получено очень мало результатов для таких гамильтонианов в том случае, когда ядро частично-интегрального оператора является невырожденным. В настоящее время представляет интерес получение точных результатов хотя бы для частных случаев, т. е. для нелокальных потенциалов с вырожденными ядрами. Так как двухчастичные и трехчастичные уравнения Шредингера легко разрешимы для нелокальных взаимодействий, их часто используют в ядерной физике и в многочастичных проблемах. Они также используются систематически вместе с уравнениями Фаддеева и Вайнберга для систем трех частиц.
2. Модельный оператор. Через 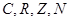 обозначим множества всех комплексных, вещественных, целых и натуральных чисел, соответственно. Пусть
обозначим множества всех комплексных, вещественных, целых и натуральных чисел, соответственно. Пусть 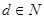 и
и 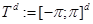 —
— 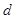 - мерный куб с соответствующим отождествлением противоположных граней. Всюду в работе
- мерный куб с соответствующим отождествлением противоположных граней. Всюду в работе 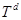 рассматривается как абелева группа, в которой операции сложения и умножения на вещественное число введены как операции сложения и умножения на вещественное число в
рассматривается как абелева группа, в которой операции сложения и умножения на вещественное число введены как операции сложения и умножения на вещественное число в 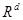 по модулю
по модулю 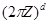 . Например, если
. Например, если
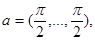
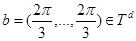 ,
,
то
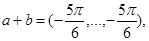
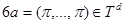 .
.
Пусть 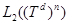 — гильбертово пространство квадратично интегрируемых (комплекснозначных) функций, определенных на
— гильбертово пространство квадратично интегрируемых (комплекснозначных) функций, определенных на 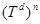 ,
, 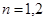 .
.
Рассмотрим модельный оператор 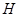 , действующий в гильбертовом пространстве
, действующий в гильбертовом пространстве 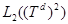 по формуле
по формуле
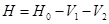 ,
,
где операторы 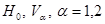 определяются по правилам:
определяются по правилам:
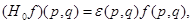
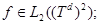
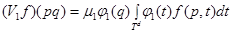 ;
;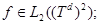
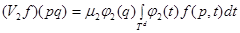 ;
; 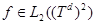 .
.
Здесь 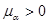 ,
, 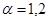 ,
, 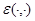 вещественно-непрерывные функции на
вещественно-непрерывные функции на 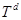 и
и 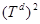 , соответственно. Видно, что нелокальные операторы взаимодействия
, соответственно. Видно, что нелокальные операторы взаимодействия 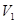 и
и 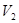 являются частичными интегральными операторами с вырожденными ядрами ранга 1.
являются частичными интегральными операторами с вырожденными ядрами ранга 1.
Можно легко проверить, что в этих предположениях модельный оператор 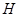 является ограниченным и самосопряженным в гильбертовом пространстве
является ограниченным и самосопряженным в гильбертовом пространстве 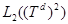 .
.
Известно, что в импульсном представлении трехчастичный дискретный оператор Шредингера 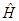 действует в гильбертовом пространстве
действует в гильбертовом пространстве 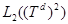 . После выделения полного квазиимпульса системы
. После выделения полного квазиимпульса системы 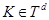 оператор
оператор 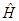 разлагается в прямой операторный интеграл (см. например [3, 4])
разлагается в прямой операторный интеграл (см. например [3, 4])

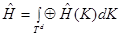 ,
,
где ограниченный самосопряженный оператор 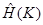 ,
, 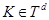 действует в гильбертовом пространстве
действует в гильбертовом пространстве 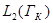 (
(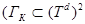 - некоторое многообразие). Отметим, что модельный оператор
- некоторое многообразие). Отметим, что модельный оператор 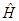 обладает основными спектральными свойствами трехчастичного дискретного оператора Шредингера
обладает основными спектральными свойствами трехчастичного дискретного оператора Шредингера 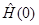 , см. например [6–8].
, см. например [6–8].
Учитывая выше сказанные факты оператора 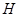 можно рассматривать как модельный оператор, ассоциированный системой трех частиц на решетке, взаимодействующих с помощью парных нелокальных потенциалов.
можно рассматривать как модельный оператор, ассоциированный системой трех частиц на решетке, взаимодействующих с помощью парных нелокальных потенциалов.
3. Уравнение Вайнберга для собственных функций. Пусть 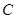 — множество комплексных чисел. Положим
— множество комплексных чисел. Положим
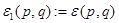 ,
, 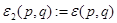 ,
,
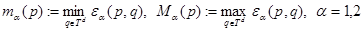 .
.
При каждом фиксированным 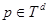 определим регулярную в
определим регулярную в 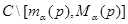 функцию
функцию
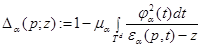 .
.
Обозначим через 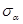 множество тех точек
множество тех точек 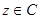 , для которых имеет место равенство
, для которых имеет место равенство 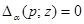 хотя бы для одной
хотя бы для одной 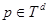 и
и
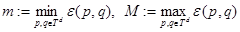 .
.
Следующая теорема описывает местоположение существенного спектра модельного оператора 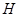 .
.
Теорема 1. Для существенного спектра 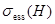 модельного оператора
модельного оператора 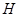 справедливо равенство
справедливо равенство 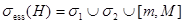 .
.
Определение. Множества 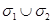 и
и 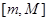 называются, соответственно, «двухчастичной» и «трехчастичной» ветвями существенного спектра модельного оператора
называются, соответственно, «двухчастичной» и «трехчастичной» ветвями существенного спектра модельного оператора 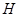 .
.
При каждом 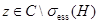 рассмотрим интегральный оператор
рассмотрим интегральный оператор 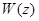 действующий в пространстве
действующий в пространстве 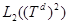 с ядром
с ядром
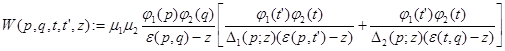
(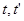 - переменное интегрирование).
- переменное интегрирование).
Верна следующая теорема.
Теорема 2. Если 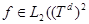 – cобственная функция, соответствующая собственному значению
– cобственная функция, соответствующая собственному значению 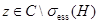 оператора
оператора 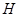 , то
, то 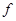 удовлетворяет уравнению
удовлетворяет уравнению 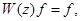 обычно называемое уравнением Вайнберга.
обычно называемое уравнением Вайнберга.
Доказательство. Пусть 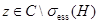 собственное значение оператора
собственное значение оператора 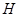 и
и 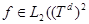 — соответствующая собственная функция. Тогда
— соответствующая собственная функция. Тогда 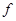 удовлетворяет уравнению
удовлетворяет уравнению
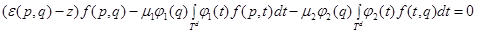 (1)
(1)
Так как 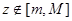 , то из уравнения (1) для
, то из уравнения (1) для 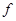 имеем
имеем
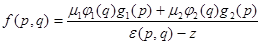 , (2)
, (2)
где
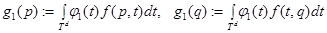 . (3)
. (3)
Подставляя выражение (2) для 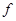 в равенств (3) и учитывая
в равенств (3) и учитывая 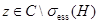 получим
получим
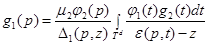 , (4)
, (4)
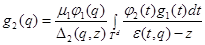 . (5)
. (5)
Теперь в равенстве (2) вместо 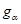 подставляя её выражение (4) и (5), затем пользуясь выражением (3) получим уравнение Вайнберга
подставляя её выражение (4) и (5), затем пользуясь выражением (3) получим уравнение Вайнберга 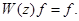 Теорема 2 доказана.
Теорема 2 доказана.
Отметим, что из положительности оператора 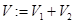 вытекает, что оператор
вытекает, что оператор 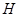 не имеет собственных значений на
не имеет собственных значений на 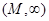 . Далее, если при некоторых предположениях оператор
. Далее, если при некоторых предположениях оператор 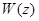 принадлежит классу Гильберта-Шмидта при
принадлежит классу Гильберта-Шмидта при 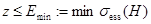 и операторнозначная функция
и операторнозначная функция 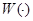 является непрерывным в равномерной операторной топологии в
является непрерывным в равномерной операторной топологии в 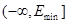 , то пользуясь теоремой 2 можно доказать [5] конечность дискретного спектра оператора
, то пользуясь теоремой 2 можно доказать [5] конечность дискретного спектра оператора 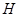 , расположенного в
, расположенного в 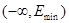 .
.
Литература:
1. Д. Р. Яфаев. О конечности дискpетного спектpа тpехчастичного опеpатоpа Шpедингеpа // Теор. мат. физ., — 1975, — Т. 25, — № 2, — С. 185–195.
2. Г. М. Жислин. О конечности дискретного спектра операторов энергии квантовых систем многих частиц // ДАН СССР, — 1972, — Т. 207, — № 1, 25–28.
3. Ж. И. Абдуллаев, С. Н. Лакаев. Конечность дискретного спектра трехчастичного оператора Шредингера на решетке // Теор. мат. физ., — 1997, — Т. 111, — № 1, — С. 94–108.
4. С. Н. Лакаев, М. Э. Муминов. Существенный и дискретный спектр трехчастичного оператора Шредингера на решетке // Теор. мат. физ., — 2003, — Т. 135, — № 3, 478–503.
5. Т. Х. Расулов, Р. Т. Мухитдинов. Конечность дискретного спектра модельного оператора, ассоциированного с системой трех частиц на решетке // Известия вузов. Математика. — 2014, — № 1, С. 61–70.
6. S. Albeverio, S. N. Lakaev, R. Kh. Djumanova. The essential and discrete spectrum of a model operator associated to a system of three identical quantum particles // Rep. Math. Phys., — 2009, — V. 63, — no. 3, 359–380.
7. S. Albeverio, S. N. Lakaev, Z. I. Muminov. On the number of eigenvalues of a model operator associated to a system of three-particles on a lattices. Russ. J. Math. Phys., — 2007, — V. 14, — no. 4, — P. 377–387.
8. Т. Х. Расулов. Асимптотика дискретного спектра одного модельного оператора, ассоциированного с системой трех частиц на решетке // Теор. мат. физ., — 2010, -Т. 163, — № 1, 34–44.

