Рассматривается самосопряженная обобщенная модель Фридрихса 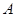 , которая ассоциирована гамильтонианом системы, состоящей из не более чем двух частиц. Обсуждается случай, когда существенный спектр оператора
, которая ассоциирована гамильтонианом системы, состоящей из не более чем двух частиц. Обсуждается случай, когда существенный спектр оператора 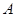 может содержать лакуны. Получено достаточное условие конечности дискретного спектра оператора
может содержать лакуны. Получено достаточное условие конечности дискретного спектра оператора 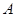 .
.
Ключевые слова: обобщенная модель Фридрихса, молекулярно-резонансной модель, блочно-операторная матрица, операторы рождения и уничтожения, лакуна существенного спектра.
В настоящей работе рассматривается гамильтониан 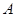 описывающий двухканальной молекулярно-резонансной модели [1–5]. В настоящей заметке найдено достаточное условие конечности дискретного спектра оператора
описывающий двухканальной молекулярно-резонансной модели [1–5]. В настоящей заметке найдено достаточное условие конечности дискретного спектра оператора 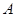 . Следует отметит, что некоторые актуальные задачи анализа, математической физики и теории вероятностей сводятся к исследованию спектра рассматриваемой модели. В [1–5] изучены спектр и резонансы аналогичных гамильтонианов.
. Следует отметит, что некоторые актуальные задачи анализа, математической физики и теории вероятностей сводятся к исследованию спектра рассматриваемой модели. В [1–5] изучены спектр и резонансы аналогичных гамильтонианов.
Через 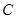 ,
, 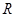 и
и 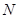 обозначим множества всех комплексных, вещественных и натуральных чисел, соответственно. Пусть
обозначим множества всех комплексных, вещественных и натуральных чисел, соответственно. Пусть 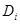 ,
, 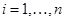 , (
, (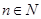 ) -ограниченная область с евклидовой мерой в
) -ограниченная область с евклидовой мерой в 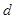 -мерном пространстве
-мерном пространстве 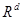 , а также
, а также 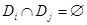 ,
, 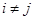 и
и 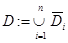 .
.
Пусть 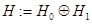 — двухканальное гильбертово пространства, состоящее из одномерного гильбертово пространства
— двухканальное гильбертово пространства, состоящее из одномерного гильбертово пространства 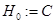 (канал 1) и ядерного гильбертово пространства
(канал 1) и ядерного гильбертово пространства 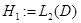 — квадратично-интегрируемых (комплекснозначных) функций, определенных на
— квадратично-интегрируемых (комплекснозначных) функций, определенных на 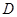 (канал 2). Элементы пространства
(канал 2). Элементы пространства 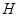 представляются как векторы
представляются как векторы 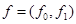 , где
, где 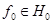 и
и 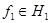 . Для двух элементов
. Для двух элементов 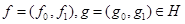 , их скалярное произведение
, их скалярное произведение 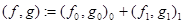 в
в 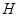 естественно определяется через скалярные произведения
естественно определяется через скалярные произведения
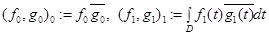 .
.
Рассмотрим гамильтониан 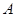 , действующий в гильбертовом пространстве
, действующий в гильбертовом пространстве 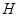 как
как 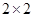 блочно-операторная матрица
блочно-операторная матрица
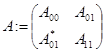 , (1)
, (1)
где матричные элементы 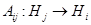 ,
, 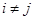 ,
, 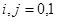 определяются по формулам
определяются по формулам
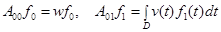 ,
,
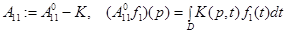 .
.
Здесь 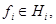
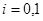 ;
; 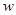 — фиксированное вещественное число,
— фиксированное вещественное число, 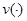 и
и 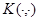 — вещественнозначные ограниченные функции на
— вещественнозначные ограниченные функции на 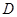 и
и 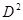 , соответственно,
, соответственно, 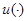 — вещественнозначная кусочно-непрерывная и ограниченная функция на
— вещественнозначная кусочно-непрерывная и ограниченная функция на 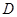 . В этих предположениях на параметры оператор
. В этих предположениях на параметры оператор 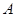 , действующий в гильбертовом пространстве
, действующий в гильбертовом пространстве 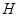 , является ограниченным и самосопряженным. При этом
, является ограниченным и самосопряженным. При этом 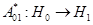 сопряженный оператор к
сопряженный оператор к 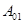 и
и
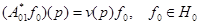 .
.
Оператор 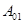 называется оператором уничтожения, а
называется оператором уничтожения, а 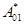 называется оператором рождения. Оператор уничтожения снижает количество частиц в заданном состоянии на единицу, а оператор рождения увеличивает число частиц в данном состоянии на единицу, и является сопряженным к оператору уничтожения. Такие операторы имеют широкое применение в квантовой механике, в частности, при изучении квантовых гармонических осцилляторов и систем многих частиц [6].
называется оператором рождения. Оператор уничтожения снижает количество частиц в заданном состоянии на единицу, а оператор рождения увеличивает число частиц в данном состоянии на единицу, и является сопряженным к оператору уничтожения. Такие операторы имеют широкое применение в квантовой механике, в частности, при изучении квантовых гармонических осцилляторов и систем многих частиц [6].
Следует отметить, что обобщенная модель Фридрихса 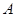 также называется двухканальной молекулярно-резонансной моделью [1], которая ассоциирована гамильтонианом системы, состоящей из не более чем двух частиц. Например, если
также называется двухканальной молекулярно-резонансной моделью [1], которая ассоциирована гамильтонианом системы, состоящей из не более чем двух частиц. Например, если
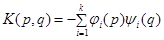 ,
,
то эти частицы взаимодействуют как с помощью нелокального потенциала, так и с помощью операторов рождения и уничтожения. В работе [2] показано существование и аналитичность собственных значений оператора типа (1) в случае 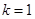 .
.
Цель нашей работы — нахождение достаточного условия конечности дискретного спектра обобщенной модели Фридрихса 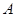 , определенной по формуле (1). При этом результат полученной для
, определенной по формуле (1). При этом результат полученной для 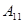 в работе [7] переносятся на
в работе [7] переносятся на 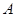 . Заметим, что характер спектра, структура резольвенты, вид собственных векторов дискретного и непрерывного спектра, проблема существования и полноты волновых операторов полностью или частично изучались в литературе применительно к обычной модели Фридрихса
. Заметим, что характер спектра, структура резольвенты, вид собственных векторов дискретного и непрерывного спектра, проблема существования и полноты волновых операторов полностью или частично изучались в литературе применительно к обычной модели Фридрихса 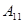 (см. [8–10]).
(см. [8–10]).
На протяжении всей работы под обозначениями 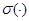 ,
, 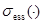 и
и 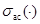 понимаются спектр, существенный спектр и абсолютно непрерывный спектр ограниченного самосопряженного оператора, соответственно.
понимаются спектр, существенный спектр и абсолютно непрерывный спектр ограниченного самосопряженного оператора, соответственно.
Так как оператор 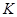 является компактным, а операторы
является компактным, а операторы 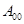 ,
, 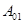 ,
, 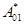 являются одномерными, из теоремы Вейля о существенном спектре следует, что существенный спектр
являются одномерными, из теоремы Вейля о существенном спектре следует, что существенный спектр 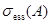 оператора
оператора 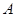 совпадает со спектром оператора
совпадает со спектром оператора 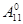 . При этом
. При этом 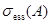 состоит из замыкания области значений
состоит из замыкания области значений 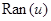 функции
функции 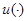 , т. е.
, т. е.
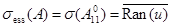 .
.
Отметим, что существенный спектр оператора 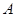 может содержит множеству с изолированной точкой
может содержит множеству с изолированной точкой 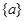 такое, что
такое, что 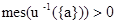 (
(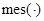 означает лебегово мера). Следовательно, мы не сможем утверждать, что существенный спектр оператора
означает лебегово мера). Следовательно, мы не сможем утверждать, что существенный спектр оператора 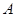 является абсолютно непрерывным. Например, если
является абсолютно непрерывным. Например, если 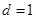 ,
, 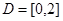 ,
, 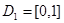 ,
, 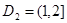 и функция
и функция 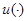 определена по формуле
определена по формуле
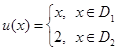 ,
,
то 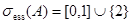 . Так как
. Так как 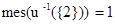 , то имеет место равенство
, то имеет место равенство 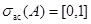 .
.
Более того, если 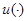 является кусочно абсолютно непрерывная функция на
является кусочно абсолютно непрерывная функция на 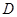 и
и 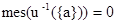 при всех
при всех 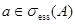 , то имеем
, то имеем 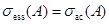 .
.
Далее, мы будем дополнительно предполагать, что оператор 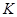 является положительным. Положительный квадратный корень
является положительным. Положительный квадратный корень 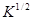 оператора
оператора 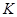 имеет вид
имеет вид
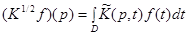 ,
,
где через 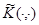 формально обозначено ядро оператора
формально обозначено ядро оператора 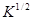 и является квадратично-интегрируемой функцией на
и является квадратично-интегрируемой функцией на 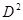 .
.
Пусть 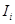 — единичный оператор в
— единичный оператор в 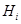 ,
, 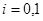 и
и 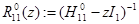 . В исследованиях дискретного спектра оператора
. В исследованиях дискретного спектра оператора 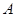 основную роль играет компактный (симметризованный) оператор
основную роль играет компактный (симметризованный) оператор 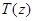 ,
, 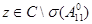 , действующий в
, действующий в 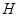 как
как 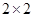 блочно-операторная матрица
блочно-операторная матрица
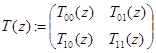
где матричные элементы 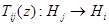 ,
, 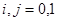 определяются по формулам
определяются по формулам
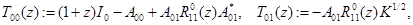
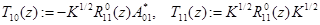 .
.
Основным результатом данной заметки является следующая теорема.
Теорема 1. Пусть 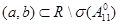 и оператор-функция
и оператор-функция 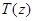 при
при 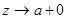 и
и 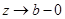 сходится равномерно к некоторым операторам
сходится равномерно к некоторым операторам 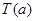 и
и 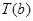 , соответственно. Тогда оператор
, соответственно. Тогда оператор 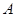 на интервале
на интервале 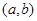 может иметь лишь конечное число собственных значений.
может иметь лишь конечное число собственных значений.
Заметим, что в теореме 1 компактность оператора 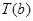 является достаточным условием для конечности дискретного спектра оператора
является достаточным условием для конечности дискретного спектра оператора 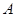 на
на 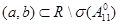 . Для обоснования этого факта рассмотрим следующий пример.
. Для обоснования этого факта рассмотрим следующий пример.
Пример. Пусть 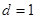 и
и 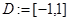 . Опишем свойства параметр-функций, входящих в (1) для этого случая:
. Опишем свойства параметр-функций, входящих в (1) для этого случая: 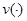 — вещественнозначная непрерывная функция на
— вещественнозначная непрерывная функция на 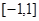 , а функции
, а функции 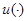 и
и 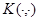 определяются равенствами
определяются равенствами 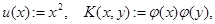 где
где 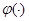 — вещественнозначная непрерывная функция на
— вещественнозначная непрерывная функция на 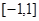 . Тогда
. Тогда 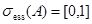 и оператор
и оператор 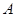 имеет не более двух (не более одного) простых собственных значений, лежащих левее
имеет не более двух (не более одного) простых собственных значений, лежащих левее 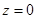 (правее
(правее 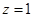 ), см. [4]. Далее, найдя вид оператора
), см. [4]. Далее, найдя вид оператора 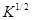 , после несложных вычислений получаем, что матричные элементы
, после несложных вычислений получаем, что матричные элементы 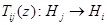 ,
, 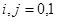 семейства операторов
семейства операторов 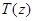 ,
, 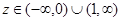 , имеют вид:
, имеют вид:
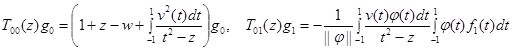 ,
,
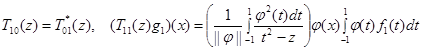 .
.
Ниже покажем, что равномерная сходимость семейства операторов 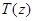 ,
, 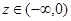 при
при 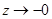 зависят от поведений функций
зависят от поведений функций 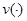 и
и 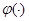 в малой окрестности точки
в малой окрестности точки 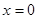 . Очевидно, что если
. Очевидно, что если 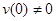 , то интеграл
, то интеграл
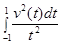 (2)
(2)
расходится. Поэтому при 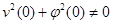 , семейство операторов
, семейство операторов 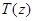 ,
, 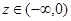 не сходится равномерно ни к какому оператору при
не сходится равномерно ни к какому оператору при 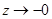 .
.
Пусть теперь 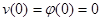 . Допустим, что существуют константы
. Допустим, что существуют константы 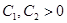 и
и 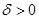 такие, что
такие, что 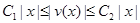 и
и 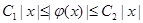 при
при 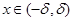 . Тогда интеграл (2) сходится. В этом случае семейство операторов
. Тогда интеграл (2) сходится. В этом случае семейство операторов 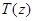 ,
, 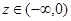 сходится равномерно к оператору
сходится равномерно к оператору 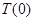 при
при 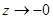 . Аналогичные рассуждения верны при
. Аналогичные рассуждения верны при 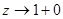 .
.
Благодарность. Работа поддержана программой фонда Эйнштейна при международном математическом обществе. Автор приносит благодарность Берлинской математической школе и институту Вейерштрасса по прикладному анализу и стохастики за приглашение, поддержку и гостеприимство.
Литература:
1. A. K. Motovilov, W. Sandhas, Y. B. Belyaev. Perturbation of a lattice spectral band by a nearby resonance // J. Math. Phys., — 2001. — V. 42. — P. 2490–2506.
2. С. Н. Лакаев, Ш. М. Латипов. О существовании и аналитичности собственных значений двухканальной молекулярно-резонансной модели // Теор. и матем. физика, — 2011. — Т. 169. — №. 3. — С. 341–351.
3. M. I. Muminov, T. H. Rasulov. The Faddeev Equation and Essential Spectrum of a Hamiltonian in Fock Space // Methods Func. Anal. Topology, — 2011. -V. 17. — no. 1. — P. 47–57.
4. Т. Х. Расулов. Исследование существенного спектра одного матричного оператора // Теор. и матем. физика, — 2010, — Т. 164, — № 1, — С. 62–77.
5. Т. Х. Расулов. Уравнение Фаддеева и местоположение существенного спектра модельного оператора нескольких частиц // Известия вузов. Математика. — 2008, — № 12, С. 59–69.
6. R. P. Feynman. Statistical mechanics: a set of lectures (2nd ed.). Reading, Massachusetts: Addison-Wesley, 1998, p. 151.
7. М. Э. Муминов. О выражение числа собственных значений модели Фридрихса // Матем. заметки, — 2007, — Т. 82, — № 1, С. 75–83.
8. K. O. Friedrichs. Uber die Spectralzerlegung einee Integral operators // Math. Ann., — 1938, — V. 115, — no. 1, P. 249–272.
9. К. Фридрихс. Возмущение спектра операторов в гильбертовом пространстве. М., 1969.
10. K. O. Friedrichs. On the perturbation of continuous spectra // Comm. Pure Appl. Math., — 1948, — V. 1, — no. 4, — P. 361–406.

