Область применения математических методов не ограничена: все виды движения материи могут изучаться математически. Однако роль и значение математического метода в различных случаях различны. Никакая определённая математическая схема не исчерпывает всей конкретности действительных явлений, поэтому процесс познания конкретного протекает всегда в борьбе двух тенденций; с одной стороны, выделения формы изучаемых явлений и логического анализа этой формы, с другой стороны, вскрытия моментов, не укладывающихся в установленные формы, и перехода к рассмотрению новых форм, более гибких и полнее охватывающих явления. Если же трудности изучения какого-либо круга явлений состоят в осуществлении второй тенденции, если каждый новый шаг исследования связан с привлечением к рассмотрению качественно новых сторон явлений, то математический метод отступает на задний план; в этом случае диалектический анализ всей конкретности явления может быть лишь затемнён математической схематизацией. Если, наоборот, сравнительно простые и устойчивые основные формы изучаемых явлений охватывают эти явления с большой точностью и полнотой, но зато уже в пределах этих зафиксированных форм возникают достаточно трудные и сложные проблемы, требующие специального математического исследования, в частности создания специальной символической записи и специального алгоритма для своего решения, то мы попадаем в сферу господства математического метода.
И действительно, математика используется повсеместно, для решения задач из самых разных областей. В том числе, и для решения задач строительства. Существуют сложные строительные задачи — такие, например, как расчет прочности несущих элементов здания. Здесь могут применяться громоздкие математические формулы, объемные таблицы сопротивления материалов и емкие расчеты. Есть задачи средней сложности, а есть задачи применимые на занятиях по математике, для изучения математического аппарата, но через задачу практического характера. Следует отметить, что одним из самых важных условий при постройке нового дома всегда было правильно разметить углы. Но как получить прямой угол? Ответ на этот вопрос дал греческий математик Пифагор, сформулировав и доказав свою известную теорему. С тех пор задача разметки углов в профессиональном строительстве решается именно через прямоугольный треугольник. Еще одна строительная задача, при решении которой применяется математика — замер площадей сложной формы. Как видим, математика очень эффективно решает любые строительные задачи, связанные не только с разметкой и обмером, но и выделенных сложных задач возникающих в строительстве.
На примере одной из таких задач хотелось бы подчеркнуть значимость математики в профессиональной деятельности будущих строителей. Для ее решения студент должен обладать:
- определенным уровнем сформированности профессионального умения, а именно, умения определять распределение в строительных изделиях математическими методами;
- иллюстрации связей раздела «Уравнения математической физики» с дисциплиной специализации «Конструкции из дерева и пластмасс»;
- развитием профессиональной мотивации при изучении данного раздела математики.
Задача. Одна из граней длинного прямоугольного бруса (рис.1) поддерживается при заданной температуре, на остальных гранях Т=0. Найти установившуюся температуру в произвольной точке внутри бруса.
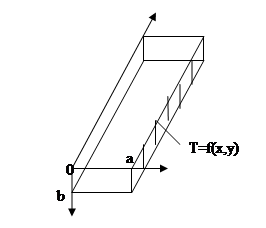
Рис. 1
На основе анализа решения задачи составляется математическая модель задачи в виде уравнения теплопроводности:
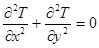 ,
,
удовлетворяющего двум парам краевых условий:
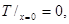
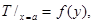
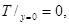
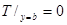 .
.
Применяя метод Фурье к решению данного уравнения, студенты находят функцию 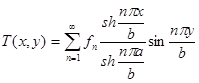 , где
, где 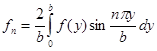 , определяющую установившуюся температуру в произвольной точке внутри бруса.
, определяющую установившуюся температуру в произвольной точке внутри бруса.
Анализ решения задачи позволяет определить уровень сформированности профессиональных качеств личности инженера-строителя: профессиональной мотивации, взаимосвязи математики (в частности уравнения теплопроводности и его решения методом Фурье) со строительной дисциплиной «Конструкции из дерева и пластмассы», умения определять распределение температур в строительных изделиях математическими методами. А также применять их в дальнейшем на производстве, поэтому вклад математического образования в строительной отрасли очень велик.
Литература:
1. Крымская Ю. А., Титова Е. И., Ячинова С. Н. Профессиональная подготовка строителей через решение математических задач// Современные проблемы науки и образования. 2014. № 2.
2. Куимова Е. И., Куимова К. А., Титова Е. И. Прикладная направленность курса математики в строительном вузе// Молодой ученый. 2014. № 11. С. 390–391.
3. Крымская Ю. А., Титова Е. И., Ячинова С. Н. Построение математических моделей в прикладных задачах// Молодой ученый. 2013. № 12 (59). С. 3–6.
4. Несис Е. И. Методы математической физики: Учебн. пособие для студентов физ-мат. фак. пед. ин-тов. — М.: Просвещение, 1977. — 198с.

