Как известно, числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с некоторым числом, называется арифметической прогрессией. А числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на некоторое отличное от нуля постоянное число, называется геометрической прогрессией. Из определения арифметической и геометрической прогрессий, мы видим, что данные прогрессии основаны на арифметических действиях суммы (разности) и умножения (деления). Возникает вопрос: существует ли прогрессия, которая основана на действии возведение в степень число. Отвечая на этот вопрос, автором был определен новый вид прогрессии — показательная прогрессия.
Определение 1 [1]. Пусть дана последовательность положительных чисел
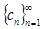
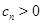
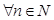. (1)
Последовательность (1), первый член которой отличен от единицы, называется показательной прогрессией, если ее каждый член, начиная со второго, равен предыдущему, возведенному в положительную степень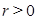 
(
).
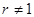Таким образом,
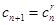
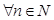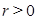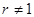, (), (2)
где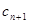 
и 
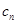соответственно n- и n+1-й члены прогрессии; r — знаменатель показателя прогрессии, которая вычисляется по формуле
.
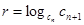Показательную прогрессию будем обозначать следующим образом:
.
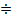
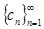В данной статье был определен новый вид числовой прогрессии — показательно-геометрическая прогрессия. Доказаны некоторые свойства введенной прогрессии, как общая формула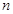 
-го члена, формула нахождения знаменателя и знаменателя показателя прогрессии, характеристическое свойство, а также установлена связь с показательной прогрессией.
Прежде чем дать определение рассматриваемой прогрессии, хотелось бы поговорить о характеристическом свойстве показательной прогрессии. В [1] в качестве характеристического свойства взята следующая теорема.
Теорема. Для каждого члена показательной прогрессии, начиная со второго, выполняется равенство
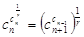. (3)
Хотя соотношение (3) и выражает связь между соседними тремя членами показательной прогрессии, оно связано со знаменателем показателя прогрессии r. Однако если вспомнить, характеристические свойства арифметической и геометрической прогрессий, которые не зависят соответственно от разности и знаменателя, можно сказать, что существует соотношение, которое будет связывать подряд идущих три члена показательной прогрессии, не завися от знаменателя показателя. Покажем ее с помощью следующей теоремы.
Теорема 1 (характеристическое свойство показательной прогрессии). Для каждого члена показательной прогрессии, начиная со второго, выполняется равенство
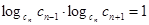. (4)
Доказательство. По определению показательной прогресси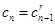и
и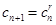 
.
Отсюда следует, что
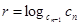или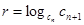
т. е.
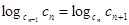
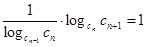
или
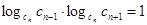
что и требовалось доказать.
Перейдем к основной части статьи.
Определение 2. Пусть дана последовательность положительных чисел
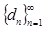
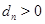
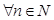. (5)
Последовательность (5), первый член которой отличен от единицы, называется показательно-геометрической прогрессией, если ее каждый член, начиная со второго, равен предыдущему, возведенному в одну и ту же положительную степень 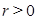(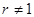) и умноженному на одно то же положительное число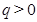 
.
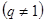Таким образом,
, (), , 
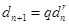
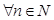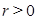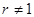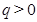
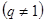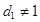(6)
где 
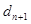и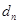 
соответственно n- и n+1-й члены прогрессии; q — знаменатель, r — знаменатель показателя прогрессии, которая вычисляется по формуле.
Показательную прогрессию будем обозначать следующим образом:
.
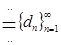Пример 1. Следующая прогрессия является показательно-геометрической с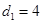 
, 
, 
:
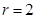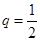4, 8, 32, 512, 131072,....
Из определения 2 следуют замечания.
Замечание 1. Если в показатеьльно-геометрической прогрессии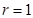 
, то можно получить геометрическую прогрессию.
Замечание 2. Если в показатеьльно-геометрической прогрессии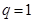 
, то можно получить показательную прогрессию.
Определим знаменатель показателя показательно-геометрической прогрессии. По (6) запишем n+1-ый и n+2-ой члены прогресси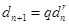и
и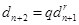 
.
Разделим почленно данные равенства и прологарифмируем обе части получившегося равенства по основанию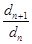 
.
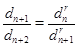или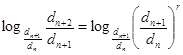 
.
А от этого следует наше искомое равенство
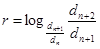. (7)
Замечание 3. Если 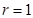, то из (7) можно получить характеристическое свойство геометрическрй прогрессии, т. е.
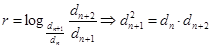при .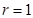
Рассмотрим следующие равенства
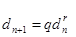және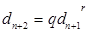 
.
Отсюда следует, что
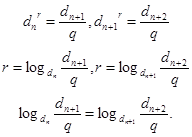
По свойству логарифмов
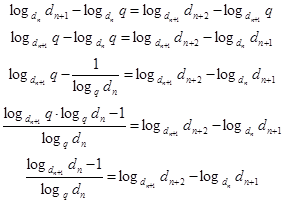
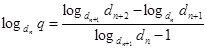(8)
Итак, знаменатель показательно-геометрической прогрессии q можно найти по формуле (8).
Замечание 4. Если q=1, то из (8) можно получит характеристическое свойство показательной прогрессии.
.
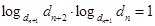Формула (2) неудобна тем, что для вычисления п-го члена необходимо знать все предыдущие члены прогрессии. Выведем формулу общего члена показательно-геометрической прогрессии. По определению показательной прогрессии
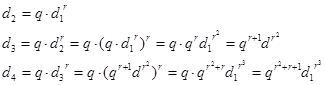
Мы видим, что здесь есть закономерность: индекс каждого члена прогрессии больше показателя степени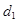 
на единицу, и больше степени многочлена — показателя q на две единицы. Поэтому мы можем предположить, что n+1-й член прогрессии вычисляется по формуле
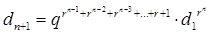
или
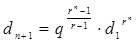. (9)
Доказательство данной формулы можно провети методом математической индукции.
Теорема 2.1. Пусть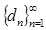 
показательно-геометрическая прогрессия, тогда последовательность 
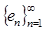, n-член которой определяется следующим образом
,
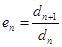будет показательной прогрессией.,
Для 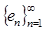ее характеристическое свосйтво будет следующее равенство:
.
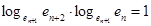Если выполнить следующие замены:
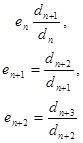
Тогда получим:
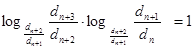. (10)
(10) формулу можно принять за харктеристическое свосйтво показательно-геометрической прогрессии.
Литература:
1. Н. К. Гульманов / Определение нового вида прогрессии, основанной на операции возведения в степень, и изучение ее основных свойств / Н. К. Гульманов, Н. А. Марчук // «Высокое качество и лидерство в образовании»: сборник докладов Международной научно-практической конференции (13–15 ноября 2013 года)/ АОО «Назарбаев Интеллектуальные школы». Часть 1. — Астана, 2013. — С. 120–124
