Библиографическое описание:
Давронов, Ж. Р. Экстремальная функция и представление нормы функционала погрешности / Ж. Р. Давронов. — Текст : непосредственный // Молодой ученый. — 2017. — № 25 (159). — С. 4-6. — URL: https://moluch.ru/archive/159/44896/ (дата обращения: 08.09.2024).
Функция 
из 
называется экстремальной функцией для функционала погрешности 
, если выполняется равенство
.
Пространство 
является гильбертовым и скалярное произведение в этом пространстве дается формулой 
По теореме Рисса любой линейно непрерывный функционал 
в гильбертовом пространстве представляется в виде скалярного произведения
(1)
для любой функции из 
. Здесь 
— функция из пространства 
, определяется единственным образом по функционалу 
и является его экстремальной функцией. Интегрируя по частям выражения в правой части равенства (1) и используя периодичность функций 
и 
, получаем равенство
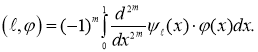
Таким образом, экстремальная функция 
является обобщенным решением уравнения
(2)
с граничными условиями
Для экстремальной функции имеет место следующая
Теорема 1.1. Явное выражение для экстремальной функции 
функционала погрешности 
определяется формулой
(3)
где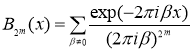 
является полиномом Бернулли, 
– константа.
Доказательство. Используем формулы преобразования Фурье, данный в [1], cвертка двух функций определяется формулой
Применяя к обеим частям равенства (2) преобразование Фурье и используя известные формулы (см. [17])
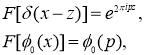
получаем
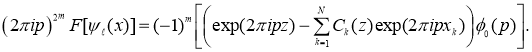(4)
В силу (4) правая часть равенства (4) равна нулю в начале координат. Следовательно, обе части уравнения (4) делятся на 
.
Функция 
определяется из (4) до выражения
Но, как известно, периодическое решение однородного уравнения, соответствующего уравнению (2), является константой, тогда все члены, кроме 
до последнего выражения, должны быть отброшены. Таким образом, из (4) имеем
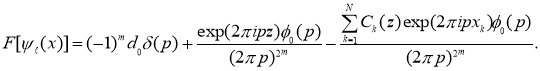
Отсюда, с учетом
и 
имеем
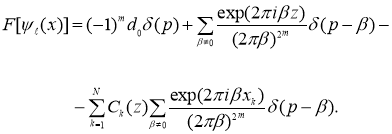
Применяя к обеим частям последнего равенства обратное преобразование Фурье, получаем
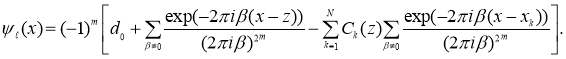Отсюда, используя определение полинома Бернулли
, получим (3)
Литература:
-
Соболев С. Л. Введение в теорию кубатурных формул. -М.: Наука, 1974.
-
Шадиметов Х. М. Дискретный аналог дифференциального оператора
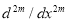и его построение// Вопросы вычислительной и прикладной математики: Сб. науч. тр. Ташкент, ИК АН Узбекистана, -вып. 79, 1985. –С. 22–35. arXiv:1001.0556 [NA.math].
-
Шадиметов Х. М. Оптимальные решетчатые квадратурные и кубатурные формулы в пространствах Соболева. Дис. докт. физ.-мат. наук. -Ташкент, 2002. -218 с.
Основные термины (генерируются автоматически): экстремальная функция, правая часть равенства, скалярное произведение, функция.
Похожие статьи
— скалярное произведение в , определенное равенством и согласованное с нормой в ; — билинейная форма, заданная на , , ; — шар в радиуса с центром в нуле; — носитель суммируемой функции
Умножая скалярно обе части последнего равенства на и меняя затем в правой части порядок интегрирования, получим. Переходя здесь к пределу при и , получим соотношение. . Теорема доказана для любой вектор функции из пространства...
Если значения интеграла (4) принять за скалярное произведение векторных функций и , то превратится в гильбертово пространство, в общем случае — неполное.
Интегрируя почленно левую и правую части формулы Лагранжа (6), получим формулу Грина.
Скачать Часть 1 (pdf). Библиографическое описание
, . Здесь и вещественнозначные непрерывные функции на .
, их скалярное произведение определяется по равенству: , где.
со скалярным произведением.
Задача 2.Найти такие значения и , чтобы выполнялось равенство (5).
Теорема 2.Функция. является экстремальной функцией для кубатурной формулы (1) и .
Скачать Часть 1 (pdf). Библиографическое описание
Пусть имеется евклидово пространство, элементами которого являются функции аргумента , со скалярным произведением .
Экстремальная функция и представление нормы функционала погрешности. Обсуждение.
Скачать Часть 1 (pdf). Библиографическое описание
Сначала дадим определение квадратичного числового образа оператора и некоторые информации о нем (для подробности смотрите работу [5]). Пусть и -скалярное произведение и норма в , соответственно.
Скачать Часть 1 (pdf). Библиографическое описание
, то их скалярное произведение определяется по равенству
Если рассмотрим симметричные функции [2], то получается стандартное бозонное пространства Фока, в случае антисимметричных функций получается...
в гильбертовом пространстве вектор-функций , рассматриваемых как вектор-столбцы, со скалярным произведением.
Об одной задаче определения правой части линейного дифференциального уравнения четвертого порядка.
— скалярное произведение в , определенное равенством и согласованное с нормой в ; — билинейная форма, заданная на , , ; — шар в радиуса с центром в нуле; — носитель суммируемой функции
Умножая скалярно обе части последнего равенства на и меняя затем в правой части порядок интегрирования, получим. Переходя здесь к пределу при и , получим соотношение. . Теорема доказана для любой вектор функции из пространства...
Если значения интеграла (4) принять за скалярное произведение векторных функций и , то превратится в гильбертово пространство, в общем случае — неполное.
Интегрируя почленно левую и правую части формулы Лагранжа (6), получим формулу Грина.
Скачать Часть 1 (pdf). Библиографическое описание
, . Здесь и вещественнозначные непрерывные функции на .
, их скалярное произведение определяется по равенству: , где.
со скалярным произведением.
Задача 2.Найти такие значения и , чтобы выполнялось равенство (5).
Теорема 2.Функция. является экстремальной функцией для кубатурной формулы (1) и .
Скачать Часть 1 (pdf). Библиографическое описание
Пусть имеется евклидово пространство, элементами которого являются функции аргумента , со скалярным произведением .
Экстремальная функция и представление нормы функционала погрешности. Обсуждение.
Скачать Часть 1 (pdf). Библиографическое описание
Сначала дадим определение квадратичного числового образа оператора и некоторые информации о нем (для подробности смотрите работу [5]). Пусть и -скалярное произведение и норма в , соответственно.
Скачать Часть 1 (pdf). Библиографическое описание
, то их скалярное произведение определяется по равенству
Если рассмотрим симметричные функции [2], то получается стандартное бозонное пространства Фока, в случае антисимметричных функций получается...
в гильбертовом пространстве вектор-функций , рассматриваемых как вектор-столбцы, со скалярным произведением.
Об одной задаче определения правой части линейного дифференциального уравнения четвертого порядка.
