В статье представлены результаты моделирования нагружения балки статически неопределимой конструкции в среде SolidWorks. Дано описание состояния конструкции при различных частотных режимах в соответствии с полученными эпюрами напряжения vonMisesи плотности энергии деформации.
Ключевые слова: балка, частота, напряжение vonMises, деформация
Статически неопределимой конструкцией является геометрически неизменяемая система, в которой реакции связей, характеризующие деформации не могут быть определены с помощью одних уравнений статики [1]. Статическая неопределимость рамы может быть выражена вследствие: а) большого числа внешних связей; б) наличия замкнутых контуров; в) наличия более трех внешних связей. Расчет напряжений, перемещений и деформаций статически неопределимых конструкций выполняют аналитическим методом или в специальных программных комплексах инженерного анализа (CAE — системы). Программные комплексы позволяют решать задачи различного характера, с высокой точностью имитируя реальные процессы с возможностью получения результатов исследования в виде интерактивных эпюр, графиков, таблиц и т. д.
При действии периодической нагрузки на элементы системы возникают вынужденные колебания конструкции [2, с. 4]. Напряженно-деформированное состояние конструкции от характера воздействия вынужденных колебаний определяется гармоническим анализом. На основании проведенного анализа можно судить об устойчивости системы.
Линейный гармонический анализ статически неопределимой рамы выполнялся в программной среде SolidWorks Simulation. Для расчета построена 3D модель рамы, общий вид и габаритные размеры которой представлены на рисунке 1.
Решение производилось в программе Direct Sparse. Были приняты следующие свойства имитационного моделирования: количество частот — 10; нижний частотный предел — 0 Гц (Цикл/сек.); верхний частотный предел — 20 Гц (Цикл/сек.); количество точек для каждой частоты — 15; ширина полосы для каждой частоты — 0,4; интерполяция — логарифмическая; демпфирование по Релею (α = 0,02, β = 0,04).
Высокая точность полученных результатов решения задачи обеспечивалась разбиением (сетка на основе кривизны) модели на 71823 элемента (112261 узел).
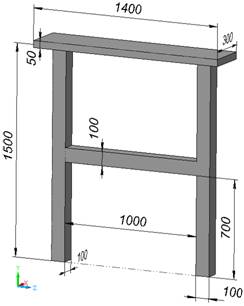
Рис. 1. Габаритные размеры твердотельной модели рамы (масса — 475,8 кг)
В качестве материала модели была принята углеродистая сталь обыкновенного качества. Основные физико-механические свойства материала отображены в таблице 1.
Таблица 1
|
Параметр |
Значение параметра |
|
Предел текучести (σт), Н/м2 |
2,20594 · 108 |
|
Предел прочности при растяжении (σв. р.), Н/м2 |
3,99826 · 108 |
|
Модуль упругости (E), Н/м2 |
2,1 · 1011 |
|
Коэффициент Пуассона (μ) |
0,28 |
|
Массовая плотность (ρ), кг/м3 |
7800 |
|
Модуль сдвига (G), Н/м2 |
7,9 · 1010 |
|
Коэффициент теплового расширения (β), К-1 |
1,3 · 10–5 |
На горизонтальную балку рамы действовала нормальная сила величиной 800 Н (рисунок 2). Крепление конструкции осуществлялось за основания двух вертикальных стоек.
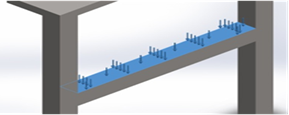
Рис. 2. Поверхность и направление приложения нормальной силы на балку рамы
Количество частотных шагов решения задачи — 106. Для каждого расчетного шага определено значение частоты: 1–93 шаги менее 1 Гц; 94 шаг — 1,37498 Гц; 95 шаг — 1,88468 Гц; 96 шаг — 2,42862 Гц; 97 шаг — 3,01478 Гц; 98 шаг — 10,0003 Гц; 99 шаг — 16,3457 Гц; 100 шаг — 16,9858 Гц; 101 шаг — 17,5719 Гц; 102 шаг — 18,1159 Гц; 103 шаг — 18,6256 Гц; 104 шаг — 19,1068 Гц; 105 шаг — 19,5628 Гц; 106 шаг — 20 Гц.
Результаты решения задачи на различных частотных шагах представлены эпюрами напряжения von Mises (рисунок 3 а, б, в) и плотности энергии деформации ε (рисунок 4 а, б, в) рамы.
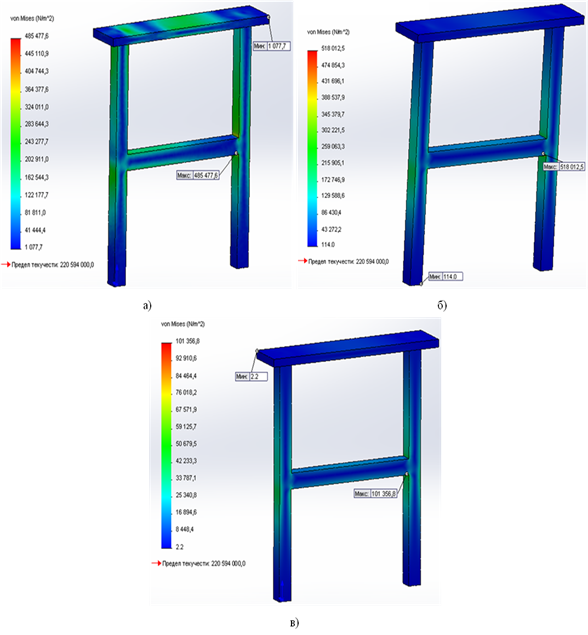
Рис. 3. Эпюры напряжения von Mises σ конструкции: а) шаг 2-х частотный — 5,307 · 10–6 Гц; б) шаг 60-и частотный — 0,000466 Гц; в) шаг 106-и частотный — 20 Гц. Единица измерения — Н/м2
Напряжение von Mises представляет собой величину напряжения, рассчитанную исходя из составляющих напряжения. Оно предоставляет информацию, достаточную для оценки надежности конструкции [3]. На 2-х частотном шаге отмечено напряженное состояние всех элементов рамы под действием нагрузки. Максимальное напряжение σmax (485477,6 Н/м2) — в местах соединения горизонтальной балки и вертикальных стоек. При частоте 0,000466 Гц наблюдается сосредоточение напряжения конструкции только в местах соединения, σmax составляет 518012,5 Н/м2. Дальнейшее увеличение частоты до 20 Гц приводит к уменьшению σmax на рассматриваемом шаге до 101356,8 Н/м2.
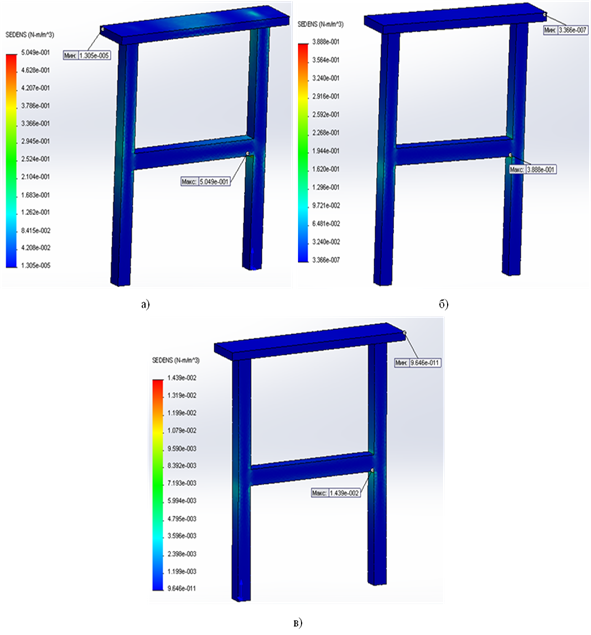
Рис. 4. Эпюра плотности энергии деформации ε конструкции: а) шаг 2-х частотный — 5,307 · 10–6 Гц; б) шаг 60-и частотный — 0,000466 Гц; в) шаг 106-и частотный — 20 Гц. Единица измерения — Н-м/м3
Плотность энергии деформации — отношение энергии к тому объему в котором она заключена. На эпюрах максимальная плотность энергии деформации εmax определена в местах соединения горизонтальной балки и вертикальных стоек. Отмечено, что на интервале частот от 5,307 · 10–6 до 20 Гц плотность энергии деформации уменьшается с 0,505 до 0,014 Н-м/м3.
Характер изменения напряжения von Mises и плотности энергии деформации рамы на всех частотных шагах представлены на рисунках 5 и 6.
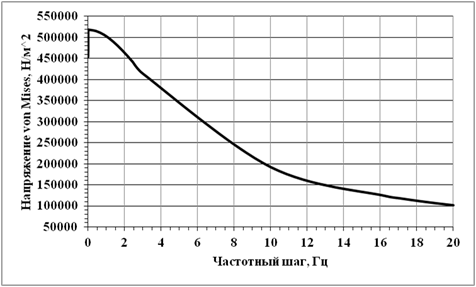
Рис. 5. Зависимость напряженного состояния рамы от величины частоты
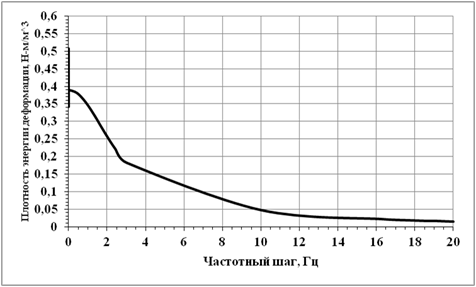
Рис. 6. Зависимость плотности энергии деформации рамы от величины частоты
Коэффициенты массового участия важны для определения соответствия вычисленных мод (форм) колебаний для решения динамических задач с движением основания. Список коэффициентов массового участия в глобальных направлениях X, Y и Z, нормализованных относительно общей массы модели представлены в таблице 2.
Таблица 2
Коэффициенты массового участия
|
Номер режима |
Частота, Гц |
Направление X |
Направление Y |
Направление Z |
Период, сек |
|
1 |
0,00024333 |
0,062634 |
0,0031471 |
0,00011146 |
4109,6 |
|
2 |
0,0003374 |
0,61464 |
0,0029802 |
2,8941 · 10–5 |
2963,8 |
|
3 |
0,00036217 |
0,0011418 |
0,2119 |
0,025341 |
2761,2 |
|
4 |
0,00046862 |
0,001604 |
0,78142 |
0,011392 |
2133,9 |
|
5 |
0,00048713 |
0,00054528 |
0,0004313 |
0,96185 |
2052,8 |
|
6 |
0,00056644 |
0,31944 |
0,00012683 |
0,0012801 |
1765,4 |
|
7 |
58,147 |
6,5267 · 10–22 |
4,4119 · 10–26 |
1,4126 · 10–24 |
0,017198 |
|
8 |
97,135 |
3,4953 · 10–26 |
1,6159 · 10–23 |
5,4488 · 10–24 |
0,010295 |
|
9 |
105,16 |
1,6147 · 10–25 |
6,8327 · 10–24 |
4,2804 · 10–24 |
0,0095092 |
|
10 |
137,02 |
2,4062 · 10–24 |
3,2562 · 10–25 |
9,0134 · 10–26 |
0,0072983 |
|
Сумма X = 1 |
Сумма Y = 1 |
Сумма Z = 1 |
В таблице, номера режимов указывают на порядковые номера мод. Направления X, Y и Z — значения коэффициентов массового участия в глобальных направлениях соответствующих плоскостей для каждой моды.
По результатам исследования были сделаны следующие выводы:
1) с увеличением резонансных частот в интервале от 5,307 · 10–6 до 20 Гц, уменьшаются максимальные значения напряжения von Mises и плотности энергии деформации конструкции более чем в 5 раз;
2) определены расположение и величина максимальных значений напряжения von Mises и плотности энергии деформации конструкции;
3) получены значения коэффициентов массового участия в 3 координатных направлениях.
Литература:
1. Статически неопределимая система [Электронный ресурс] URL: http://ru.wikipedia.org/wiki/ %D1 %F2 %E0 %F2 %E8 %F7 %E5 %F1 %EA %E8_ %ED %E5 %EE %EF %F0 %E5 %E4 %E5 %EB %E8 %EC %E0 %FF_ %F1 %E8 %F1 %F2 %E5 %EC %E0 (дата доступа: 25.07.2014).
2. Леонтьев Н. В. Применение системы ANSYS к решению задач модального и гармонического анализа. Учебно-методический материал по программе повышения квалификации «Информационные системы в математике и механике». Нижний Новгород. 2006. — 101 с.
3. Von Mises Stress [Электронный ресурс] URL: http://www.plm-forum.ru/forum/viewtopic.php?t=3658 (дата доступа: 25.07.2014).

