В настоящее время очень стремительно развиваются методы расчета на устойчивость, а также деформационные, динамические и аэродинамические расчёты, имеющие особо важное значение для вантовых и висячих мостов, основой которых служат системы из растянутых кабелей. Статья посвящена расчёту собственных колебаний ванты методом явного интегрирования уравнений движений без учёта внешних воздействий. Выполнено сравнение предлагаемого метода с общеизвестными алгоритмами определения характеристик собственных колебаний вант. Также произведен расчет системы с учётом нелинейности в растягивающих усилиях и отмечено, что данный факт значительно влияет на конечные параметры колебаний вант.
Ключевые слова: колебания вант, вантовые мосты, собственные колебания, динамический расчёт, растянутый кабель, нелинейное поведение.
Для описания колебания вант используется известное уравнение струны, описывающее малые поперечные колебания однородной натянутой струны. Исторически это первый пример уравнения математической физики — гиперболического вида:
,
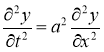где a — константа, отражающая свойства струны; x — координата вдоль струны; t — время; y(x,t) — отклонение струны от положения равновесия.
Данное уравнение не учитывает нелинейное поведение вант, что подтверждается в многих работах [2, 3]. Под нелинейным поведение подразумевается, геометрическая нелинейность, возникающая в вантовых элементах, вследствие этого продольное усилие 
изменяется по длине элемента.
Рассмотрим ванту длиной l, шарнирно закрепленную по концам с опорами в одном уровне равномерно загруженной собственным весом. Реализуем метод явного интегрирования уравнений движения для расчёта собственных колебаний.
Решаемые технические задачи:
– проанализировать характеристики колебаний, полученные по известным зависимостям и методом интегрирования;
– выполнить расчет собственных колебаний с учётом геометрической нелинейности.
Для решения поставленной задачи приняты необходимые исходные данные (таблица). Расчет колебаний будет представлен как в линейной постановке, так и с учетом геометрической нелинейности. Для первого случая натяжение
принимается постоянным по всей длине струны.
Исходные данные
|
Длина ванты |
Удельный вес |
Площадь поперечного сечения |
Модуль Юнга |
Скорость распространения волны |
Натяжение |
|
100,0 |
7850,0 |
0,012 |
2,06∙108 |
300,0 |
4905,0 |
, м
, кг/м3
, м2
, кН/м2
, м/с
, кН
Разделим ванту на 
равных частей длиной 
, тем самым получаем 
узлов в нашей системе. Так как колебания изменяются во времени, зададимся временным шагом:
Рис. 1. Расчетная схема
Для того, чтобы определить собственные колебания струны, зададим системе возмущение в момент времени 
в виде начальной скорости 
. Струну длинной 
разделим на равных частей с шагом , тем самым получаем узлов в нашей системе. Анализ колебаний вантового элемента произведем для первой формы колебаний. На Рис. 2 показаны три первые формы колебаний струны.
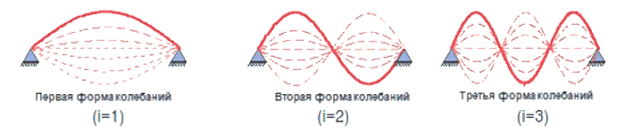
Рис. 2. Основные формы колебаний
Первую форму колебаний описывает закон синусоиды, тогда в каждом узле вычислим начальную скорость 
по формуле:
,
где
— начальная скорость в i-ом узле (
);
— форма колебаний в виде синусоиды;
— расстояние от левой опоры до i-го узла.
Имея скорости в явном виде, вычислим во всех узлах системы смещение 
:
.
Рассмотрим расчетную схему более детально, выделив два смежных элемента и вырежем узел, указан все действующие силы (см. Рис. 3).
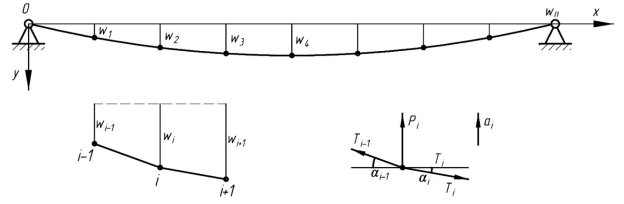
Рис. 3. Схема к расчету равнодействующей силы P(i)
Основываясь на предположении, что отклонения струны от равновесия малы, сделаем ряд упрощений:
-
Длина участка струны в деформированном состоянии практически равна длине участка в положении равновесия, поэтому добавочным напряжением вследствие удлинения струны можно пренебречь. Следовательно, силы
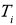и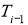 
по модулю равны силе натяжения струны .
-
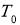Углы наклона 𝛼 малы, поэтому tg𝛼 ≈ sin𝛼 ≈ 𝛼 и, следовательно, можно положить
, 
.
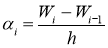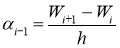Спроецируем все действующие силы в узле на ось Y и получим выражение для определения силы действующей на узловую сосредоточенную массу и соответствующее ей ускорение:
;
Далее вычислим приращение скорости 
и определим результирующую скорость на данном временном шаге:
Принимая 
вычислим шаг по длине и времени 
. Они должны быть достаточно малыми, чтобы избежать численной погрешности.
м;
сек.
Для 
, следуя выше изложенному алгоритму, вычислим на каждом временном шаге неизвестные параметры. Данная задача решается численно с применением среды Matlab, так как расчёты получаются очень трудоемкими, в связи с малым дискретным шагом по времени 
. На основании полученных после расчета данных построим графики зависимости скорости 
и вертикальных перемещений 
от времени t (Рис. 4, 5).
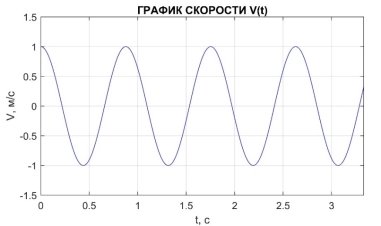
Рис. 4. График зависимости 
от 
при 
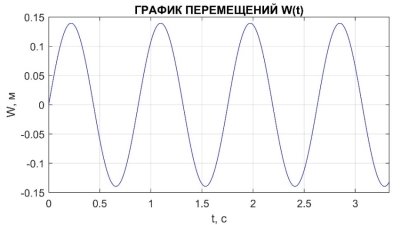
Рис. 5. График зависимости 
от при
Определим период колебаний
, это есть расстояние вдоль оси абсцисс от 0 до первого положительного экстремума (Рис. 4):
сек.
Сравним полученное расчетное значение с теоретическим. В соответствии с [4] период колебаний определяется по формуле:
,
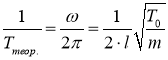Тогда 
сек.
Следует сделать вывод, что выбранный алгоритм точно описывает линейные колебания струны.
Расчёт собственных колебаний ванты сучётом геометрической нелинейности
Для учёта нелинейности, вышеизложенный алгоритм дополним определением продольного усилия 
в i-ом узле системы. Ранее мы сделали допущение и не учитывали дополнительные напряжения, возникающие, вследствие, удлинения струны. Учтем это использовав закон Гука, тогда получим следующее:
, где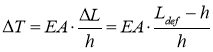 
,
,
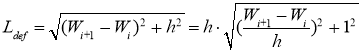где 
— длина элемента после удлинения, 
— приращение длины участка h, вследствие изменения геометрии системы; EA — продольная жесткость ванты.
Подставив
в искомое выражение получим выражение для определения натяжения с учетом геометрической нелинейности:
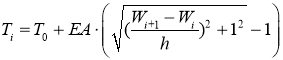
Также измениться сила, действующая на узловую сосредоточенную массу m:
На Рис. 6 представлено сравнение скорости и перемещений в линейной постановке задачи и с учетом геометрической нелинейности.
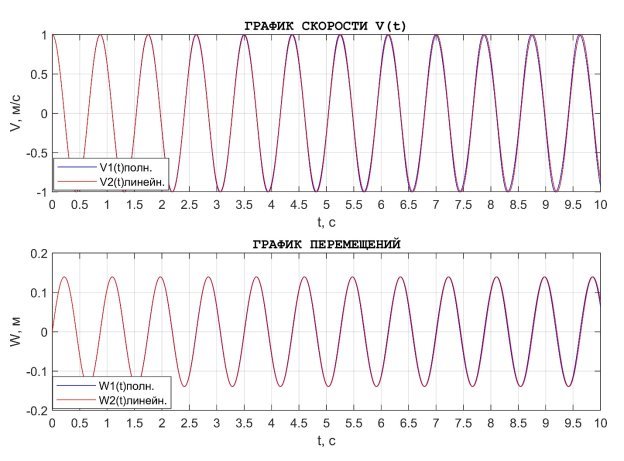
Рис. 6. Графики скорости и вертикальных перемещений колебаний ванта от при 
Как видим из сравнительных графиков, учёт нелинейности в продольных усилиях не оказывает значительного влияния на колебания струны в данных условиях при задании возмущения в виде начальной скорости. Периоды собственных колебаний составляют: без учета нелинейности 
сек., с учётом нелинейности 
сек.
Метод интегрирования уравнений движения можно использовать для исследования нелинейных колебаний вант, в том числе и с внешним сосредоточенным демпфером при различных внешних воздействиях.
Литература:
- Вантовые мосты / А. А. Петропавловский, Е. И. Крыльцов, Н. Н. Богданов и др.; Под ред. А. А. Петропавловского. — М.: Транспорт, 1985. — 224 с.
- Меркин Д. Р. Введение в механику гибкой нити. — М.: Наука. Главная редакция физико-математической литературы, 1980. — 240 с.
- Качурин В. К. Гибкие нити с малыми стрелками. — М.: Гос. издательство технико-теоретической литературы, 1956. — 224 с.
- Cable stays. Recommendation of French interministerial commission on Prestressing. — CIP Setra, 2002. — 197 с.
