В статье приводится методика определения прогибов изгибаемых железобетонных элементов без предварительного напряжения арматуры на основе нелинейной деформационной модели с использованием двухлинейной расчетной диаграммы состояния бетона. Приводятся результаты численного анализа изменения прогибов изгибаемых элементов в зависимости от внешней нагрузки, определенные по методикам СНиП 2.03.01–84*, СП 63.13330.2018 и деформационной модели и сопоставляются с экспериментальными данными.
Ключевые слова: изгибаемый железобетонный элемент, деформационная модель, кривизна оси, нормальные трещины, прогибы.
Ограничение прогибов железобетонных конструкций связано с необходимостью обеспечения условий для нормальной эксплуатации зданий и сооружений, в которых эти конструкции использованы. При определении прогибов, подлежащих ограничению, следует учитывать нагрузки, зависящие от требований, вызвавших эти ограничения. В частности, при ограничении прогибов по эстетико-психологическим требованиям прогибы определяются при действии только постоянных и длительных нагрузок, т. е. допускается кратковременное превышение прогибов сверх допустимых по этим требованиям. При этом прогиб отсчитывается от прямой, соединяющей точки опирания конструкций, т. е. выгиб, вызванный предварительным обжатием, не учитывается.
Прогибы железобетонных конструкций определяются по общим правилам строительной механики в зависимости от изгибных, сдвиговых и осевых деформационных характеристик железобетонных элементов.
Для определения кривизны сечения принимается двухлинейная диаграмма b — b сжатого и растянутого бетона. Для изгибаемых элементов без напрягаемой арматуры стадия работы без трещин в растянутой зоне занимает не более 20 % от предела несущей способности [1]. Поэтому эксплуатационная стадия работы, как правило, сопровождается образованием и допустимым раскрытием нормальных трещин.
Кривизна оси на участках с трещинами в растянутой зоне в общем случае определяется через деформации крайней сжатой грани бетона b и высоту сжатой зоны х из решения уравнений равновесия внешних и внутренних усилий на основе расчетной схемы, когда для сжатого бетона принимается двухлинейная диаграмма b–b, а сопротивление растянутого бетона не учитывается, как это показано на рис.1.
Деформации растянутой арматуры, при гипотезе плоских сечений принимается как усредненная величина между деформацией арматуры в сечениях с трещиной и между трещинами с использованием коэффициента s по выражению
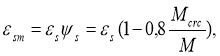 (1)
(1)
где s — деформация арматуры в сечении с трещиной;
Mcrc и M — момент соответствующий образованию трещин, и изгибающий момент при котором определяются деформации.
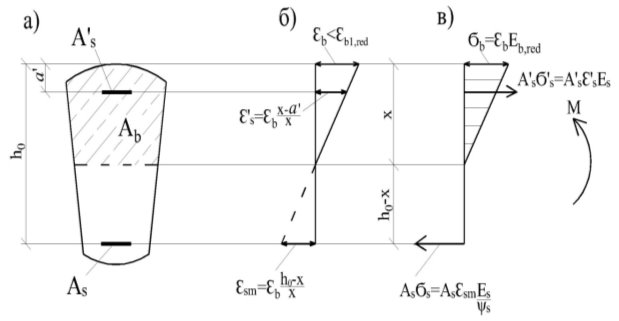
Рис. 1. К определению кривизны для участка с трещинами изгибаемого элемента: а — схема сечения; б — эпюра усредненных деформаций арматуры и бетона; в — эпюра напряжений в сечении с трещиной
Для изгибаемых элементов без предварительного напряжения прямоугольного сечения значение х можно определить из уравнения равновесия продольных усилий (см. рис.1) по выражению
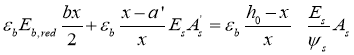 (2)
(2)
Как видно одно неизвестное b можно исключить и принимая обозначения ![]() получаем квадратное уравнение с одним неизвестным х
получаем квадратное уравнение с одним неизвестным х
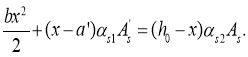 (3)
(3)
Решение квадратного уравнения запишем в виде
![]() (4)
(4)
где ![]()
Неизвестное b определяется из уравнения равновесия изгибающих моментов относительно нейтральной оси. Это уравнение имеет вид
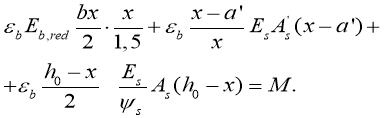 (5)
(5)
Тогда деформации сжатой грани будут равны
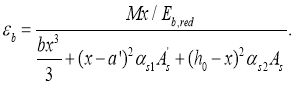 (6)
(6)
Знаменатель выражения (6) представляет собой момент инерции приведенного сечения, определенной относительно нейтральной оси Ired с учетом приведенной площади сжатой и растянутой арматуры.
В общем виде кривизну оси сечений с трещинами можно записать
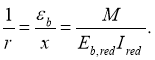 (7)
(7)
Для сечений с трещинами изгибная жесткость во многом определяется изгибающим моментом, а также деформациями сжатой грани бетона, высотой сжатой зоны и неравномерностью распределения деформаций в растянутой арматуре.
Численные исследования проводились по трем методикам — СНиП 2.03.01–84*; СП 63.13330.2012 и на основании деформационной модели с использованием двухлинейной диаграммы состояния бетона.
Результаты численных исследований сопоставлялись с имеющимися экспериментальными данными. Достаточно большой экспериментальный материал содержится в работе Панькова Е. Н. [2]. В качестве опытных образцов были приняты железобетонные балки прямоугольного сечения шириной 16см и высотой 20.5, 28.5 и 36.5см, для соответствующих серий. Использовался тяжелый бетон с компенсированной усадкой. Для армирования образцов без предварительного напряжения использовалась арматура класса А400. Нагружение опытных образцов производилось двумя сосредоточенными силами в пролете, с образованием зоны чистого изгиба.
Сопоставления показали, что начиная с уровня нагрузки 0.7–0.8Mult расхождение с опытными данными в значениях прогибов возрастают по всем методикам, т. е. теоретические данные отстают от практического роста прогибов. Эти закономерности наблюдаются в опытных образцах с доминирующими изгибными деформациями (2, а).
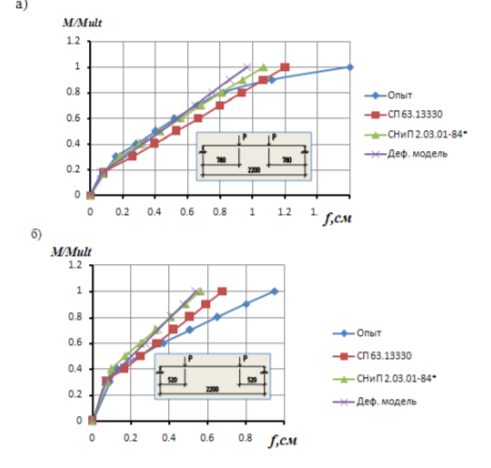
Рис. 2. Зависимость опытных [2] и теоретических прогибов от изгибающего момента для балок загруженный в третях (а) и в четвертях (б) пролета
Для балок с меньшим пролетом среза наблюдается удовлетворительная сходимость по прогибам всех методик с опытными данными до образования трещин и до уровня нагрузки 0.4Mult. При дальнейшем увеличении нагрузки (изгибающего момента) хорошая сходимость с опытными данными наблюдается в расчетных прогибах по методике СП 63.13330 до уровня нагрузки 0.6–0.7 Mult. Методика СНиП 2.03.01–84* и деформационная модель дают более заниженные значения прогибов до 20 %. Очевидно, что фактическое нарастание неупругих деформаций при уровнях нагрузки близкой к пределу несущей способности, опережает их теоретический учет. Причем расхождения могут достигать 40 %.
Таким образом, можно сделать выводы:
- Методика СП 63.13330 по определению прогиба изгибаемого элемента с учетом образования нормальных трещин имеет наименьший процент расхождения с приведенными опытными данными.
- Для определения прогиба изгибаемого элемента на стадиях близких к потере несущей способности следует учесть интенсивное снижение жесткости сечения за счет частичного разрушения в зоне максимальных усилий и развития неупругих деформаций в бетоне сжатой зоны и растянутой арматуре.
Литература:
- Кодыш Э. Н., Никитин И. К., Трекин Н. Н. Расчет железобетонных конструкций из тяжелого бетона по прочности, трещиностойкости и деформациям. — Издательство АСВ, Москва, 2010г.352с.
- Паньков Е. Н. Особенности работы изгибаемых конструкций из бетона с компенсированной усадкой при действии поперечных сил. — Диссертация канд. техн. наук. — Москва, 2005г. 160с.

