Решением задачи идентификации определяются параметры привода с упругими связями. Дается методика построения динамической модели сложной колебательной управляемой модели. Определяются коэффициенты жесткости и демпфирования привода.
Ключевые слова: объекты на подвижном основании, управление, моделирование, синтез, оптимизация упруго-вязких связей.
Во многих практических случаях определение параметров динамической системы, в том числе и параметров привода представляет значительные трудности. Ниже предлагается комбинированный способ определения параметров сложных колебательных систем, в основе которого лежит сравнение операторов системы, полученных по результатам нормальной эксплуатации и решением задач идентификации в узком смысле (по заданной динамической модели).
Решение задач идентификации предполагает нахождение приближенного оператора в системе по синхронным измерениям входной и выходной величин в процессе нормальной эксплуатации. Но при этом имеет место неоднозначность динамической модели системы, что не позволяет при необходимости осуществить ее доработку, то есть решить задачу ее синтеза. В связи с этим представляется целесообразным решение одновременно с общей задачей идентификации задачи идентификации в узком смысле.
Предлагается следующая методика построения динамической модели объекта:
- определение спектрального состава ошибки системы по результатам нормальной эксплуатации (в том числе, вибрационной карты конструктивных элементов);
- определение собственных частот колебаний конструктивных элементов объекта на основе поверочных расчетов на жесткость, проведенных на этапе проектирования;
- выделение подсистем объекта, собственные частоты которых лежат в спектральном диапазоне ошибки;
- построение динамической модели.
Влияние конструктивных элементов на точность управления, особенно по скорости, требует значительных усилий для систем, работающих в области резонансных частот. Поэтому многое определяется интуицией проектировщика в процессе настройки системы управления [1…5].
Для иллюстрации определим параметры упругих связей привода системы, динамическая модель которой приводится к случаю стабилизации объекта на подвижном основании.
Линеаризованные уравнения движения системы в форме Лагранжа имеют вид:
,
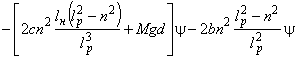 ,
,
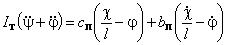 ,
,
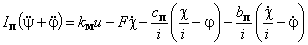 .
.
Добавив уравнение усилителя системы стабилизации
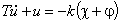
к системе уравнений, получим замкнутую систему уравнений движения.
Приняты обозначения:
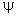 - абсолютный угол поворота платформы,
- абсолютный угол поворота платформы,
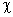 - угол поворота ротора двигателя относительно платформы,
- угол поворота ротора двигателя относительно платформы,
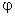 — угол поворота объекта относительно платформы,
— угол поворота объекта относительно платформы,
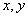 — декартовы координаты точки A платформы (лежит на оси симметрии),
— декартовы координаты точки A платформы (лежит на оси симметрии),
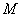 - масса всей системы,
- масса всей системы,
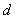 — расстояние от центра тяжести системы до точки A,
— расстояние от центра тяжести системы до точки A,
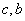 - коэффициенты жесткости и демпфирования нитей соответственно,
- коэффициенты жесткости и демпфирования нитей соответственно,
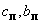 -коэффициенты жесткости и демпфирования привода соответственно,
-коэффициенты жесткости и демпфирования привода соответственно,
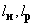 — длины нитей соответственно натуральная и в положении равновесия,
— длины нитей соответственно натуральная и в положении равновесия,
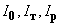 - моменты инерции соответственно всей системы относительно оси, проходящей через ее центр тяжести: объекта относительно оси вращения и ротора двигателя с приведенными к нему моментами инерции элементов редуктора;
- моменты инерции соответственно всей системы относительно оси, проходящей через ее центр тяжести: объекта относительно оси вращения и ротора двигателя с приведенными к нему моментами инерции элементов редуктора;
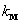 — крутизна моментной характеристики двигателя,
— крутизна моментной характеристики двигателя,
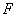 - коэффициент индуктивного сопротивления двигателя,
- коэффициент индуктивного сопротивления двигателя,
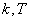 - соответственно коэффициент усиления и постоянная времени усилителя,
- соответственно коэффициент усиления и постоянная времени усилителя,
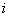 — передаточное отношение редуктора.
— передаточное отношение редуктора.
Проиллюстрируем решение задачи идентификации привода при известных параметрах привода: 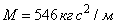 ;
; 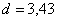 м,
м, 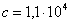 кг/м,
кг/м, 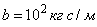 ,
, 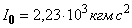 ,
, 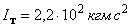 ,
, 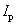 =1,53
=1,53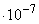
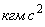 ,
, 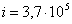 ,
, 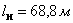 ,
, 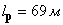 ,
, 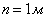 ,
, 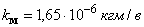 ,
, 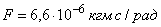 ,
, 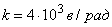 ,
, 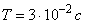 . При значениях параметров
. При значениях параметров 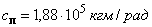 ,
, 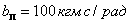 система уравнений с хорошей точностью описывает работу привода. При этом в качестве входной величины принимается угловая скорость ротора двигателя, приведенная к выходному валу редуктора
система уравнений с хорошей точностью описывает работу привода. При этом в качестве входной величины принимается угловая скорость ротора двигателя, приведенная к выходному валу редуктора 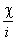 , а выходной — абсолютная угловая скорость объекта. Колебания объекта на собственной частоте
, а выходной — абсолютная угловая скорость объекта. Колебания объекта на собственной частоте 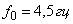 оказывает существенное влияние на ошибку системы стабилизации по скорости. Увеличение коэффициентов жесткости и демпфирования привода (в реализуемых пределах) существенно уменьшает влияние упругости привода на ошибку системы.
оказывает существенное влияние на ошибку системы стабилизации по скорости. Увеличение коэффициентов жесткости и демпфирования привода (в реализуемых пределах) существенно уменьшает влияние упругости привода на ошибку системы.
Предложенная методика легко адаптируется к исследованию подъемно-транспортных средств.
Литература:
1. Будылина Е. А., Гарькина И. А., Данилов А. М., Махонин А. С. Основные принципы проектирования сложных технических систем в приложениях / Молодой ученый. — № 5. 2013. –С.42–45.
2. Гарькина И. А., Данилов А. М., Домке Э. Р. Промышленные приложения системных методологий, теорий идентификации и управления / Вестник МАДИ. — 2009. — № 2(17). — С.77–82.
3. Будылина Е. А., Гарькина И. А., Данилов А. М. Моделирование с позиций управления в технических системах / Региональная архитектура и строительство. –2013. — № 2 (16). — С. 138–142.
4. Гарькина И. А., Данилов А. М. Управление в сложных технических системах: методологические принципы управления / Региональная архитектура и строительство. –2012. — № 1 (12). — С.39–43.
5. Будылина Е. А.,Гарькина И. А., Данилов А. М. Приближенные методы декомпозиции при настройке имитаторов динамических систем / Региональная архитектура и строительство. — 2013. — № 3(17). — C. 150–156.

