В настоящее время ведётся интенсивный поиск путей совершенствования обучения математике в вузе. Значительно стимулировало исследования в методике обучения математике использование деятельностного подхода. Идеи деятельностного подхода нашли широкое применение в психологии, педагогике, предметных методиках и др. В методике обучения математике деятельностный подход рассматривается в четырёх вариантах: создание ситуации самостоятельного открытия и усвоения способов деятельности; выделение совокупности действий, адекватных их предметному содержанию; учебная деятельность; деятельностный подход как одна из составляющих методологии методики обучения математике [1].
В условиях современной актуализации идей деятельностного подхода к обучению вариант использования его как одной из составляющих методологии обучения математике является наиболее перспективным. Его реализация предполагает выстраивание деятельности, адекватной учебному материалу и составляемой мотивационной сферой, различного рода действиями, способами деятельности, контролем и самоконтролем.
Чтобы обучать студентов первого курса математическому анализу в контексте деятельностного подходанадо определить цели изучения первых тем математического анализа с деятельностной точки зрения.
Умственное развитие студентов при изучении математического анализа идет одновременно в двух направлениях — в осмыслении абстрактного и в конкретизации абстракций. Причем второе направление нельзя квалифицировать как элементарное и менее важное. Умение видеть частное в общем, преломлять и применять общие положения к конкретным вещам является не менее трудной формой мыслительной деятельности,чем в осмыслении обстрактного.
При изучении математического анализа главная трудность состоит не в обобщении (понятия даются обычно в достаточно общей и абстрактной форме), а в конкретизации, т. е. умении видеть за математическими терминами и их определениями конкретные образы, устанавливать свойства понятий и связи между ними [2].
Очевидно, что успешность понимания основ математического анализа в вузе зависит от того, насколько хорошо первокурсник владеет понятиями и их свойствами, изученными в школьном курсе начал анализа, а также учебными действиями общего и частного характера.
Изучение любого предмета в вузе на любом курсе, а тем более на 1-курсе, имеет специфическую трудность — с чего начать? И если в содержательном плане с чего начинать понятно, то как организовать учебную деятельность студентов по усвоению изучаемого материала, выбрать методы и средства обучения — эти вопросы решаются каждым преподавателем индивидуально и часто без учета, как содержательной специфики предмета, так и реальных возможностей студентов. Как показали результаты нашего экспериментального исследования, следует начинать с обучения первокурсников «инструментальной деятельности», другими словами, вооружения их тем «инструментом», без которого невозможно изучить осмысленно основы математического анализа. Под «инструментом» мы понимаем те общие учебные действия, с помощью которых студент сможет самостоятельно постигать математический анализ.
В результате нашего исследования мы пришли к выводу, что обучение учебным действиям студентов 1-курса целесообразно начинать именно с 1- семестра и именно с тем «Действительные числа», «Функция», «Предел последовательности».
Эти темы первокурсникам поверхностно известны. Именно поверхностно, т. к. изучение опыта преподавания начал анализа в школе показывает, что усвоение основных понятий математического анализа представляет для учеников особую трудность. Поэтому появляется тенденция к поверхностному изучению, при котором основное внимание уделяется выработке простейшей техники вычислений в ущерб их осмыслению.
Исходя из этого, цели изучения раздела «Введение в анализ» в вузе мы уточнили следующим образом:
1. Подготовить первичный понятийный аппарат математического анализа для успешного изучения дифференциального и интегрального исчисления функций одной переменной (1-курс), а также последующих тем математического анализа.
2. Создать условия для формирования у студентов определенных учебных действий, необходимых для изучения математического анализа.
3. Подготовить первокурсников к самостоятельной деятельности при изучении новых разделов математического анализа и постоянного совершенствования знаний.
Разрабатывая основные положения методики обучения студентов учебным действиям при изучении математического анализа в вузе, мы исходили из целей изучения математического анализа. Учитывая специфику предмета, о которой говорилось выше, нами были выделены общие учебные действия, без которых невозможно усвоение математического анализа. Таковыми являются:
- анализ (расчленение целого объекта (метода, идеи и т. п.) на части), внутренних существенных свойств математических объектов в их закономерной взаимосвязи и т. п.;
- синтез на основе анализа и т. п.;
- сравнение (математических объектов, определений, формулировок теорем, идей доказательств, методов решения задач, алгоритмов класса задач и т. п.);
- подведение под понятие и выведение следствий;
- формулировка математических предложений на естественном языке;
- действия поиска решения задач, идеи доказательства;
- действия работы с теоремами разных видов и т. д.
Для формирования, как учебных действий, так и организации самостоятельной учебной деятельности нужно определенное средство. В качестве средств формирования учебной деятельности студентов мы рассматриваем наборы задач и задания к ним. Как пример рассмотрим следующее задание.
Задание.
1. Сформулируйте определение четной и нечетной функций. Представьте графики этих функций.
2. Исследуйте на четность и нечетность следующие функции:
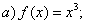б) f(x)=5; в) f(x)=0; г)
.
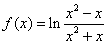3. Приведите примеры функций, являющихся и четными и нечетными. Сколько таких функций существует?
4. Докажите с помощью определения, что сумма, разность и произведение двух четных функций есть четная функция. Покажите на конкретных примерах.
5. Составьте алгоритм доказательства четности и нечетности функции.
6. Верны ли высказывания: сумма (разность) четной и нечетной функций есть:
а) четная функция, б) нечетная функция?
7. Продолжить следующие предложения, чтобы они стали верными:
а) сумма (разность) двух нечетных функций есть........функция;
б) произведение четной и нечетной функций есть......функция;
в) произведение двух нечетных функций есть.....функция;
г) частное двух четных (нечетных) функций есть.......функция.
8. Существуют ли функции, имеющие симметричную относительно нуля область определения и являющиеся:
а) четными (нечетными) и убывающими;
б) нечетными (четными) и возрастающими;
в) четными (нечетными) и положительными;
г) четными (нечетными) и неположительными;
д) нечетными и постоянными;
е) четными и постоянными. Приведите примеры.
9. Сравните четную и нечетную функцию, обратив внимание на четное или нечетное число экстремумов у этих функций. Приведите примеры.
10. При каком условии всякая функция f(х) может быть представлена как сумма четной и нечетной функций.
11. Сформулируйте достаточные условия четности и нечетности: а) линейной функции y=ax+b; б) квадратичной функции y=ax2+bx+c; в) кубической функции у = ax3 + bx2 + cx + d; г) дробно-линейной функции y=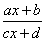
.
12. Какую функцию не надо исследовать на четность и нечетность, если известно, что она всегда ни четная, ни нечетная. Приведите конкретный пример.
Проанализируем задание с точки зрения учебных действий. При выполнении задания студент должен:
1.1 — Вспомнить (прочитать, найти в конспектах лекций, узнать у преподавателя или однокурсников и т. д.) и сформулировать определения четной и нечетной функций; представить (начертить) схематично графики четной и нечетной функций (вспомнить графики известных функций, обладающих свойством четности или нечетности); сравнить и отметить существенные отличия — для нечетной функции симметричность относительно начало координат, для четной функции симметричность относительно оси ординат;
1.2 — Применить определение к решению конкретных задач (подведение понятия под определение);
1.3 — Сконструировать (по аналогии с 1.2) примеры функций, обладающих определенным свойством.
1.4 — Поиск идеи доказательства;
- наметить общую схему доказательства с помощью определения;
- провести более общие рассуждения с помощью определения, чем в 1.2.
1.5 — Оформить предыдущие действия в виде общего алгоритма.
1.6 — Применить алгоритм доказательства для конкретной задачи, возможно привести контрпример.
1.7 — Уметь провести рассуждения из общего алгоритма и найти правильный ответ.
1.8 — Установить связи между четностью и нечетностью функции и свойством монотонности. (Чаще всего студенты это задание делают с помощью графической интерпретации и примеров конкретных функций).
1.9 — Установить связи между четностью и нечетностью функции и количеством точек экстремумов с помощью геометрической интерпретации. Задача носит исследовательский характер, так как следует рассмотреть случаи: а) точки экстремума находятся на оси ординат и б) на оси ординат нет точек экстремума.
1.10 — Задача более общая, чем 1.7 и 1.8, и обобщая результаты предыдущих задач студенты приходят к выводу, что функция должна быть определена на каком-то множестве Т и это множество симметрично относительно нуля.
1.11 — Обобщая результаты решения предыдущих задач, исследовать известные классы функций, либо накладывая условия на параметры а, b, с, и d применяя определение, либо рассматривая их как композицию четной и нечетной функций.
1.12 — Выдвинуть гипотезу о том, какая структура должна быть у функции (область определения функции является несимметричным относительно нуля промежутком, проверка гипотезы — примеры конкретных функций y=lnx, y=ax).
Решение проблемы совершенствования обучения студентов первого курса математическому анализу в контексте деятельностного подхода позволит расширить теоретические представления о содержании обучения путем выделения совокупности действий и эвристики, адекватные их предметному содержанию; разработать линии преемственности с курсом алгебры и начал анализа и условия их реализации; а также реализовать профессионально-педагогическую направленность обучения математики в вузе посредством решения задач, позволяющих осуществить мотивационное обеспечение общеобразовательного курса математики, умение проводить правдоподобные рассуждения, «открывать» новые способы решения задач, эвристические приемы, осуществлять выбор знаний для решения конкретной задачи и т. п.
Литература^
1. Епишева О. Б. Технология обучения математике на основе деятельностного подхода. М.: «Просвещение». 2003.-223с.
2. Мордкович А. Г. Методические проблемы изучения элементов математического анализа в общеобразовательной школе// Математика в школе. 2002. — № 9. 2–12 с.
